11类NCERT解决方案-第2章关系和功能–练习2.2

问题1：让A = {1,2,3，…，14}。通过R = {(x，y)：3x – y = 0，其中x，y∈A}定义从A到A的关系R。写下其域，共域和范围。

解决方案：

Given, A = {1, 2, 3,…,14}. 
Here, the relation R from A to A is given by, R = {(x, y): 3x – y = 0, where x, y ∈ A} 
So, relation R = {(1,3), (2,6), (3,9), (4,12)} 

Now, We know that, the domain of a relation R is the set of all the first elements of the ordered pairs in the relation. 
So, Domain of R = {1, 2, 3, 4} 

Now, Here the complete set A is the Codomain of relation R. 
So, Co-Domain of R = {1, 2, 3, 4,….,14} 

Now, We know that, the range of a relation R is the set of all the second elements of the ordered pairs in the relation. 
So, Range of R = {3, 6, 9, 12}

问题2：通过R = {(x，y)来定义自然数集合N上的关系R：y = x + 5，x是小于4的自然数； x，y∈N}。使用花名册形式描述此关系。写下域和范围。

解决方案：

Here, the relation R is given by, R = {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈N} 
Now, As we know that the natural numbers less than 4 are 1, 2 and 3. 
So, relation R = {(1,6), (2,7), (3,8)} 

Now, We know that, the domain of a relation R is the set of all the first elements of the ordered pairs in the relation. 
So, Domain of R = {1, 2, 3} 

Now, We know that, the range of a relation R is the set of all the second elements of the ordered pairs in the relation. 
So, Range of R = {6, 7, 8}

问题3：A = {1,2,3,5}，B = {4,6,9}。通过R = {(x，y)定义从A到B的关系R：x和y之差为奇数； x∈A，y∈B}。以花名形式写R。

解决方案：

Given, A = {1, 2, 3, 5} and B = {4, 6, 9} 
Here, the relation from A to B is given by, R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B} 
So, relation R = {(1,4), (1,6), (2,9), (3,4), (3,6), (5,4), (5,6)}

问题4：图2.7显示了集合P和Q之间的关系。

(i)套组生成器形式

(ii)名册表格。

它的范围和范围是什么?

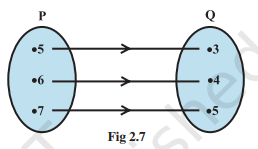
解决方案：

From the given figure, we can see that – 
P = {5, 6, 7} and Q = {3, 4, 5} 
Now, The relation between sets P and Q – 

(i) In set-builder form

R = {(x, y): y = x – 2; x ∈ P} ‘or’ R = {(x, y): y = x – 2 for x = 5, 6, 7} 

(ii) In roster form

R = {(5,3), (6,4), (7,5)} 

Now, We know that, the domain of a relation R is the set of all the first elements of the ordered pairs in the relation. 
So, Domain of R = {5, 6, 7} = P. 

Now, We know that, the range of a relation R is the set of all the second elements of the ordered pairs in the relation. 
So, Range of R = {3, 4, 5} = Q.

问题5：令A = {1,2,3,4,6}。令R为A上由-定义的关系

{(a，b)：a，b∈A，b可被a整除}。

(i)以花名册形式写R。

(ii)找到R的域。

(iii)找出R的范围。

解决方案：

Given, A = {1, 2, 3, 4, 6} 
Here, the relation R on A is given by, R = {(a, b): a , b ∈ A, b is exactly divisible by a} 

(i) The relation R in roster form will be – 
R = {(1,1), (1,2), (1,3), (1,4), (1,6), (2,2), (2,4), (2,6), (3,3), (3,6), (4,4), (6,6)} 

(ii) We know that, the domain of a relation R is the set of all the first elements of the ordered pairs in the relation. 
So, Domain of R = {1, 2, 3, 4, 6} 

(iii) We know that, the range of a relation R is the set of all the second elements of the ordered pairs in the relation. 
So, Range of R = {1, 2, 3, 4, 6}

问题6：确定由R = {(x，x + 5)：x∈{0，1，2，3，4，5}}定义的关系R的域和范围。

解决方案：

Here, the relation R is given by, R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}. 
So, relation R = {(0,5), (1,6), (2,7), (3,8), (4,9), (5,10)} 

Now, We know that, the domain of a relation R is the set of all the first elements of the ordered pairs in the relation. 
So, Domain of R = {0, 1, 2, 3, 4, 5} 

Now, We know that, the range of a relation R is the set of all the second elements of the ordered pairs in the relation. 
So, Range of R = {5, 6, 7, 8, 9, 10}

问题7：以花名册形式写关系式R = {(x，x ³ )：x是小于10的质数。

解决方案：

Here, the relation R is given by, R = {(x, x³) : x is a prime number less than 10} 
Now, As we know that the prime numbers less than 10 are 2, 3, 5 and 7. 
So, relation R = {(2,8), (3,27), (5,125), (7,343)}

问题8：令A = {x，y，z}和B = {1，2}。查找从A到B的关系数。

解决方案：

Given, A = {x, y, z} and B = {1, 2}. 
Now, number of elements in set A, n(A) = 3 
and number of elements in set B, n(B) = 2 
So, n(A × B) = n(A) × n(B) = 6. 
We know that, the number of relations from A to B = 2^{n(A × B)} = 2⁶ = 64. 

‘OR’ 

Given, A = {x, y, z} and B = {1, 2}. 
Now, A × B = {(x,1), (x,2), (y,1), (y,2), (z,1), (z,2)} 
Here, number of elements in A × B, n(A × B) = 6 
So, the number of subsets of A × B = 2⁶ = 64 
Thus, the number of relations from A to B are 64.

问题9：设R是Z上的关系，定义为R = {((a，b)：a，b∈Z，a – b是整数}。找到R的域和范围。

解决方案：

Here, the relation R is given by, R = {(a, b): a, b ∈ Z, a – b is an integer} 
As we know that the difference between any two integers is always an integer. 
So, Domain of R = Z and Range of R = Z.