📌  相关文章
📜  10类RD Sharma解决方案–第9章算术级数–练习9.6 |套装2

📅  最后修改于: 2021-06-22 19:07:00             🧑  作者: Mango

问题25.在AP中，第一项是22，第n个项是–11，前n个项的总和是66。求n和d是共同的区别。

解决方案：

问题26. AP的第一项和最后一项分别为7和49。如果其所有项的总和为420，则找到共同的差异。

解决方案：

问题27. AP的第一项和最后一项分别为5和45。如果其所有项的总和为400，则找到其共同的差异。

解决方案：

问题28. AP的前9个项之和为162。第6个项与第13个项之比为1：2。找到AP的第一个和第15个项

解决方案：

问题29.如果AP的第10项为21，而其前10个项的总和为120，则找到其第n项。

解决方案：

问题30. AP的前7个项之和为63，其后7个项之和为161。找到该AP的第28个项

解决方案：

问题31. AP的前七个项的总和为182。如果其第4和第17项的比率为1：5，则找到AP

解决方案：

问题32. AP的第n个项由(−4n + 15)给出。求出该AP的前20个词之和

解决方案：

问题33.在AP中，前十个项的总和为-150，其后十个项的总和为-550。找到AP

解决方案：

问题34. AP的前14个项之和为1505，第一个项为10。找到第25个项。

解决方案：

问题35.在AP中，第一项为2，最后一项为29，两项之和为155。找出AP的共同点

解决方案：

问题36. AP的第一项和最后一项分别为17和350。如果共同的差异是9，那么有多少个术语，它们的总和是多少?

解决方案：

问题37.查找AP –12，–9，–6，…的条款数目。 。 。 ，21。如果此AP的每个术语加1，则求出由此获得的AP的所有术语的总和。

解决方案：

问题38. AP的前n个项之和为3n 2 + 6n。查找此AP的第n个术语

解决方案：

问题39. AP的前n个项之和为5n – n 2 。查找此AP的第n个术语

解决方案：

问题40. AP的前n个项之和为4n 2 + 2n。找到此AP的第n个词

解决方案：

问题41. AP的前n个项之和为3n 2 + 4n。找到该AP的第25个学期

解决方案：

问题42. AP的前n个项之和为5n 2 + 3n。如果它的第m个项是168，则找到m的值。另外，找到该AP的第20个术语

解决方案：

问题43. AP的前q个项的总和为63q – 3q 2 。如果它的第p项为-60，求P的值。另外，找到此AP的第11个条款

解决方案：

问题44. AP的前m个项之和为4m 2 – m。如果它的第n个项是107，则找到n的值。另外，找到该AP的第21个术语

解决方案：

问题45.如果AP的前n个项之和为4n – n 2 ，那么第一个项是什么?前两个项的总和是多少?第二学期是什么?类似地，找到第三个，第十个和第n个项。

解决方案：

问题46.如果AP的前n个项之和为\frac{3n^2+7n}{2}然后找到它的第n项因此，写下它的第20个学期。

解决方案：

问题47.在AP中，前n个项的总和为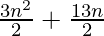\frac{3n^2}{2}+\frac{13n}{2} 。找到其第25个学期。

解决方案：

问题48.找出1到100之间的所有自然数之和，这些自然数可以被3整除。

解决方案：