Class 11 RD Sharma解决方案–第20章几何级数-练习20.3 |套装1

问题1.找到以下几何级数的总和：

(i)2、6、18，…至7个学期

解决方案：

Given G.P. has first term(a) = 2, common ratio(r) = 6/2 = 3 and number of terms(n) = 7

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1).

S₇ = 2(3⁷–1)/(3–1) 

= 2(3⁷–1)/2

= 2187–1

= 2186

Therefore, sum of 7 terms of the G.P. is 2186.

(ii)1、3、9、27，…至8个学期

解决方案：

Given G.P. has first term(a) = 1, common ratio(r) = 3 and number of terms(n) = 8

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1).

S₈ = 1(3⁸–1)/(3–1)

= 6560/2

= 3280

Therefore, sum of 8 terms of the G.P. is 3280.

(iii)1，–1/2，1/4，–1/8，…。

解决方案：

Given G.P. has first term(a) = 1, common ratio(r) = –1/2 and number of terms(n) is infinite.

We know sum of n terms of an infinite GP is given by S = a/(1–r).

S = 1/[1 – (–1/2)]

= 1/(3/2)

= 2/3

Therefore, sum of infinite terms of the G.P. is 2/3.

(iv)(a ² – b ² )，(a – b)，(a–b)/(a + b)，…至n个项

解决方案：

Given G.P. has first term(a) = (a² – b²), common ratio(r) = (a – b)/(a² – b²) = 1/(a+b) and number of terms is n.

We know sum of n terms of an infinite GP is given by S_n = a(rⁿ–1)/(r–1).

S_n = $(a^2-b^2)\left[\frac{1-(\frac{1}{a+b})^n}{1-(\frac{1}{a+b})}\right]$

= $(a^2-b^2)\left(\frac{\left(\frac{(a+b)^n-1}{(a+b)^n}\right)}{\frac{(a+b)-1}{a+b}}\right)$

= $\frac{a-b}{(a+b)^{n-2}}\left(\frac{(a+b)^n-1}{(a+b)-1}\right)$

Therefore, sum of n terms of the G.P. is $\frac{a-b}{(a+b)^{n-2}}\left(\frac{(a+b)^n-1}{(a+b)-1}\right)$.

(v)4，2，1，1/2…至10个学期

解决方案：

Given G.P. has first term(a) = 4, common ratio(r) = 2/4 = 1/2 and number of terms(n) = 10.

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1).

S₁₀ = $4\left[\frac{(\frac{1}{2})^{10}-1}{(\frac{1}{2})-1}\right]$ 

= $4\left[(\frac{1}{2})^{10}-1\right]×(-2)$

= $(-8)\left[\frac{1 - 1024}{1024}\right]$

= $\frac{1023}{128}$

Therefore, sum of 10 terms of the G.P. is $\frac{1023}{128}$.

问题2.找到以下几何级数的总和：

(i)0.15 + 0.015 + 0.0015 +…至8个词

解决方案：

Given G.P. has first term(a) = 0.15, common ratio(r) = 0.015/0.15 = 1/10 and number of terms(n) = 8.

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1).

S₈ = 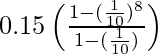$0.15\left(\frac{1-(\frac{1}{10})^8}{1-(\frac{1}{10})}\right)$

= 0.15 (10/9) (1 – 1/10⁸)

= (1/6) (1 – 1/10⁸)

Therefore, sum of 8 terms of the G.P. is (1/6) (1 – 1/10⁸).

(ii)√2+ 1 /√2+ 1 /2√2+…。至8个学期

解决方案：

Given G.P. has first term(a) = √2, common ratio(r) = (1/√2)/√2 = 1/2 and number of terms(n) = 8.

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1).

S₈ = √2[(1/2)⁸–1]/[(1/2)–1]

= √2(1–1/256)/(1/2)

= √2 (255/256) (2)

= (255√2)/128

Therefore, sum of 8 terms of the G.P. is (255√2)/128.

(iii)2/9 – 1/3 + 1/2 – 3/4 +…至5个学期

解决方案：

Given G.P. has first term(a) = 2/9, common ratio(r) = (–1/3)/(2/9) = –3/2 and number of terms(n) = 5.

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1).

S₅ = $\frac{2}{9}\left[\frac{(\frac{3}{2})^5-1}{\frac{3}{2}-1}\right]$

= $(\frac{2}{9})(\frac{275}{32})(\frac{2}{5})$

= $\frac{55}{72}$

Therefore, sum of 5 terms of the G.P. is $\frac{55}{72}$.

(iv)(x + y)+(x ² + xy + y ² )+(x ³ + x ² y + xy ² + y ³ )+…。至n个词

解决方案：

Given series can be written as,

S_n = (x + y) + (x² + xy + y²) + (x³ + x²y + xy² + y³) + . . . . to n terms

(x – y) S_n = (x + y) (x – y) + (x² + xy + y²) (x – y) . . . to n terms

(x – y) S_n = x² – y² + x³ + x²y + xy² – x²y – xy² – y³ . . . to n terms

(x – y) S_n = (x² + x³ + x⁴ + . . . n terms) + (y² + y³ + y⁴ + . . . n terms)

(x – y) S_n = x²[(xⁿ – 1)/(x – 1)] – y²[(yⁿ – 1)/(y – 1)]

S_n = [x²[(xⁿ – 1)/(x – 1)] – y²[(yⁿ – 1)/(y – 1)]]/(x – y)

Therefore, sum of n terms of series is [x²[(xⁿ – 1)/(x – 1)] – y²[(yⁿ – 1)/(y – 1)]]/(x – y).

(v)3/5 + 4/5 ² + 3/5 ³ + 4/5 ⁴ +…至n个字词

解决方案：

Given series can be written as,

S_n = (3/5 + 3/5³ + . . . to n terms) + (4/5² + 4/5⁴ +  . . . to n terms)

= $\frac{3}{5}\left[\frac{(\frac{1}{25})^n-1}{(\frac{1}{25})-1}\right]+\frac{4}{25}\left[\frac{(\frac{1}{25})^n-1}{(\frac{1}{25})-1}\right]$

= $\frac{5}{8}\left[1-\frac{1}{5^{2n}}\right]+\frac{1}{6}\left[1-\frac{1}{5^{2n}}\right]$

= $\frac{19}{24}\left[1-\frac{1}{5^{2n}}\right]$

Therefore, sum of n terms of series is $\frac{19}{24}\left[1-\frac{1}{5^{2n}}\right]$.

(六) $\frac{a}{1+i}+\frac{a}{(1+i)^2}+\frac{a}{(1+i)^3}+...\frac{a}{(1+i)^n}$

解决方案：

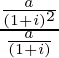Given G.P. has first term(a) = $\frac{a}{1+i}$, common ratio(r) = $\frac{\frac{a}{(1+i)^2}}{\frac{a}{(1+i)}}$ = $\frac{1}{1+i}$ and number of terms is n.

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1). 

S_n = $\frac{a}{1+i}\left[\frac{1-(\frac{1}{1+i})^n}{1-\frac{1}{1+i}}\right]$

= $(\frac{a}{1+i})(\frac{1+i}{-i})[1-(1+i)^n]$

= –a i[1–(1+i)^-n]

Therefore, sum of n terms of G.P. is –a i[1–(1+i)^-n].

(vii)1 – –a，a ² ，–a ³ ，…。 。 。 。至n项(a≠1)

解决方案：

Given G.P. has first term(a) = 1, common ratio(r) = –a and number of terms is n.

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1). 

S_n = [(–a)ⁿ–1]/(–a–1)

= [1–(–a)ⁿ]/(a+1)

Therefore, sum of n terms of G.P. is [1–(–a)ⁿ]/(a+1).

(viii)x ³ + x ⁵ + x ⁷ +。 。 。 。 n项

解决方案：

Given G.P. has first term(a) = x, common ratio(r) = x⁵/x³ = x² and number of terms is n.

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1). 

= x³[x²ⁿ–1]/[x²–1]

 Therefore, sum of n terms of G.P. is x³[x²ⁿ–1]/[x²–1].

(ix)√7+√21+3√7+。 。 。 。 n项

解决方案：

Given G.P. has first term(a) = √7, common ratio(r) = √21/√7 = √3 and number of terms = n.

We know sum of n terms of a GP is given by S_n = a(rⁿ–1)/(r–1).

S_n = √7[(√3)ⁿ–1]/(√3–1)

Therefore, sum of n terms of G.P. is √7[(√3)ⁿ–1]/(√3–1).

问题3.评估以下内容：

(一世) $\sum_{n=1}^{n=11}(2+3^n)$

解决方案：

Given summation can be written as,

S₁₁ = (2+3¹) + (2+3²) + (2+3³) + . . . . + (2+3¹¹)

= 2(11) + (3¹ + 3² + 3³ + . . . . 3¹¹)

= 2(11) + 3(3¹¹–1)/(3–1)

= 22 + 265719

= 265741

Therefore, value of the summation is 265741.

(ii) $\sum_{k=1}^{k=n}(2^k+3^{k-1})$

解决方案：

Given summation can be written as,

S_n = (2+3⁰) + (2²+3¹) + (2³+3²) + . . . . + (2ⁿ+3^n-1)

= (2¹ + 2² + 2³ + . . . . + 2ⁿ) + (3⁰ + 3¹ + 3² + . . . . + 3^n-1)

= 2(2ⁿ–1)/(2–1) + 3⁰(3ⁿ–1)/(3–1)

= 2(2ⁿ–1) + (3ⁿ–1)/2

Therefore, value of the summation is 2(2ⁿ–1) + (3ⁿ–1)/2.

(iii) $\sum_{n=2}^{n=10}4^n$

解决方案：

Given summation can be written as,

S_10-2+1 = S₉ = 4² + 4³ + 4⁴ + . . . . 4¹⁰

 = 4²(4⁹–1)/(4–1)

= 16[4⁹–1]/3

Therefore, value of the summation is 16[4⁹–1]/3. 

问题4.找到序列的总和：

(i)5 + 55 + 555 +…至n个词

解决方案：

We have S_n = 5 + 55 + 555 + ….. up to n terms.

Multiplying and dividing by 9, we get

= $\frac{5}{9}$ [9+99+999+…to n terms]

= $\frac{5}{9}$ [(10–1)+(10²–1)+(10³–1)…to n terms]

= $\frac{5}{9}$ [(10+10²+10³+….n terms) – (1+1+1+…..n terms)]

= $\frac{5}{9}\left[\frac{10(10^n-1)}{10-1}-n\right]$

= $\frac{50(10^n-1)}{81}-\frac{5n}{9}$

Therefore, the sum of the series up to n terms is $\frac{50(10^n-1)}{81}-\frac{5n}{9}$. 

(ii)7 + 77 + 777 +…至n个词

解决方案：

We have S_n = 7 + 77 + 777 + … to n terms.

Multiplying and dividing by 9, we get,

= $\frac{5}{9}$ [9+99+999+…to n terms]

= $\frac{5}{9}$ [(10–1)+(10²–1)+(10³–1)…to n terms]

= $\frac{5}{9}$ [(10+10²+10³+….n terms) – (1+1+1+…..n terms)]

= $\frac{7}{9}\left[\frac{10(10^n-1)}{10-1}-n\right]$

= $\frac{70(10^n-1)}{81}-\frac{7n}{9}$

Therefore, the sum of the series up to n terms is $\frac{70(10^n-1)}{81}-\frac{7n}{9}$.

(iii)9 + 99 + 999 +…至n个词

解决方案：

We have S_n = 9 + 99 + 999 + … to n terms. It can be written as,

= (10–1)+(10²–1)+(10³–1)…to n terms

= (10+10²+10³+….n terms) – (1+1+1+…..n terms)

= $\left[\frac{10(10^n-1)}{10-1}-n\right]$

Therefore, the sum of the series up to n terms is $\left[\frac{10(10^n-1)}{10-1}-n\right]$.

(iv)0.5 + 0.55 + 0.555 +…至n项

解决方案：

We have S_n = 0.5 + 0.55 + 0.555 + … to n terms. It can be written as,

= $\frac{5}{9}\left[\frac{9}{10}+\frac{99}{100}+\frac{999}{1000}+...n \hspace{0.1cm}terms\right]$

= $\frac{5}{9}\left[(1-\frac{1}{10})+(1-\frac{1}{100})+(1-\frac{1}{1000})+...n\hspace{0.1cm}terms\right]$

= $\frac{5}{9}\left[(1+1+1...n\hspace{0.1cm}terms)-(\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}+...n\hspace{0.1cm}terms)\right]$

= $\frac{5}{9}\left[n-\frac{(\frac{1}{10})(1-(\frac{1}{10})^n}{1-\frac{1}{10}}\right]$

= $\frac{5n}{9}-\frac{5}{81}(1-\frac{1}{10^n})$

Therefore, the sum of the series up to n terms is $\frac{5n}{9}-\frac{5}{81}(1-\frac{1}{10^n})$.

(v)0.6 + 0.66 + 0.666 +…至n项

解决方案：

We have S_n = 0.6 + 0.66 + 0.666 + … to n terms. It can be written as,

= $\frac{6}{9}\left[\frac{9}{10}+\frac{99}{100}+\frac{999}{1000}+...n \hspace{0.1cm}terms\right]$

= $\frac{6}{9}\left[(1-\frac{1}{10})+(1-\frac{1}{100})+(1-\frac{1}{1000})+...n\hspace{0.1cm}terms\right]$

= $\frac{6}{9}\left[(1+1+1...n\hspace{0.1cm}terms)-(\frac{1}{10}+\frac{1}{10^2}+\frac{1}{10^3}+...n\hspace{0.1cm}terms)\right]$

= $\frac{6}{9}\left[n-\frac{(\frac{1}{10})(1-(\frac{1}{10})^n}{1-\frac{1}{10}}\right]$

= $\frac{2n}{3}-\frac{2}{27}(1-\frac{1}{10^n})$

Therefore, the sum of the series up to n terms is $\frac{2n}{3}-\frac{2}{27}(1-\frac{1}{10^n})$.

问题5.将GP 3、3 / 2、3 / 4，…的多少项加在一起即可得到3069/512?

解决方案：

Given G.P. has first term(a) = 3, common ratio(r) = (3/2)/3 = 1/2 and sum of terms(S_n) = 3069/512.

We know sum of n terms of a G.P. is given by S_n = a(rⁿ–1)/(r–1).

=> 3069/512 = 3[1–(1/2)ⁿ] / [1–(1/2)]

=> 2(2ⁿ–1)/(2ⁿ) = 1023/512

=> 1023(2)ⁿ = 1024(2)ⁿ – 1024

=> 2ⁿ = 1024

=> n = 10

Therefore, 10 terms of the G.P. should be taken together to make 3069/512.

问题6：2 + 6 + 18 +…系列中的多少个术语。必须使总和等于728?

解决方案：

Given G.P. has first term(a) = 2, common ratio(r) = 6/2 = 3 and sum of terms(S_n) = 728.

We know sum of n terms of a G.P. is given by S_n = a(rⁿ–1)/(r–1).

=> 728 = 2[3ⁿ–1]/[3–1]

=> 3ⁿ–1 = 728

=> 3ⁿ = 729

=> n = 6

Therefore, 6 terms of the G.P. must be taken together to make the sum equal to 728.

问题7.必须使用序列√3、3、3√3，…中的多少项才能使总和为39+13√3?

解决方案：

Given G.P. has first term(a) = 2, common ratio(r) = 3/√3 = 1/√3 and sum of terms(S_n) = 39+ 13√3.

We know sum of n terms of a G.P. is given by S_n = a(rⁿ–1)/(r–1).

=> 39+13√3 = √3[3^n/2–1]/(√3–1)

=> (39+13√3)(√3–1) = √3(3^n/2–1)

=> 39√3–39+39–13√3 = 3^(n+1)/2–√3

=> 3^(n+1)/2 = 27√3 

=>  3^n/2 √3 = 27√3 

=> 3^n/2 = 27 

=> n/2 = 3

=> n = 6

Therefore, 6 terms of the G.P. must be taken to make the sum 39+ 13√3.

问题8. GP 3、6、12，…的n个项的总和为381。求n的值。

解决方案：

Given G.P. has first term(a) = 3, common ratio(r) = 6/3 = 2 and sum of terms(S_n) = 381.

We know sum of n terms of a G.P. is given by S_n = a(rⁿ–1)/(r–1).

=> 381 = 3(2ⁿ–1)/(2–1)

=> 2ⁿ – 1 = 127

=> 2ⁿ = 128

=> n = 7

Therefore, value of n is 7.

问题9. GP的公共比率是3，最后一项是486。如果这些项的总和是728，则找到第一个项。

解决方案：

Given G.P. has common ratio(r) = 3, last term(a_n) = 486 and sum of terms(S_n) = 728.

We know nth term of a G.P. is given by a_n = ar^n-1.

=> 486 = a(3)^n-1

=> 486 = a(3)ⁿ/3

=> a(3)ⁿ = 1458  . . . . (1)

We know sum of n terms of a G.P. is given by S_n = a(rⁿ–1)/(r–1).

=> 728 = a(3ⁿ–1)/(3–1)

=> 1456 = a(3)ⁿ–a

Using (1) in the equation, we get,

=> a = 1458 – 1456 = 2

Therefore, first term of the G.P. is 2.

问题10. GP的前三个项之和与前6个项之和的比率为125：152。找到共同的比率。

解决方案：

We know sum of n terms of a G.P. is given by S_n = a(rⁿ–1)/(r–1).

According to the question, we have,

=> $\frac{\frac{a(r^3-1)}{r-1}}{\frac{a(r^6-1)}{r-1}} = \frac{125}{152}$

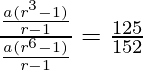
=> (r³–1)/(r⁶–1) = 125/152

=> 1/(r³+1) = 125/152

=> 125r³ + 125 = 152

=> r³ = 27/125

=> r = 3/5

Therefore, the common ratio is 3/5.

问题11：GP的第4和第7项分别为1/27和1/729。找出GP的n个项的总和

解决方案：

We know nth term of a G.P. is given by a_n = ar^n-1.

According to the question, we have,

=> ar³ = 1/27   . . . . (1)

=> ar⁶ = 1/729 . . . . (2)

Dividing (2) by (1), we get,

=> r³ = 27/729 = 1/27

=> r = 1/3

Putting r = 1/3 in (1), we get,

=> a(1/3)³ = 1/27

=> a(1/27) = 1/27

=> a = 1

We know sum of n terms of a G.P. is given by S_n = a(rⁿ–1)/(r–1).

=> S_n = 1[(1/3)ⁿ–1]/[(1/3)–1]

= 3[1–(1/3)ⁿ]/2

 Therefore, sum of n terms of the G.P. is 3[1–(1/3)ⁿ]/2.