问题1.地板砖的形状为平行四边形,底部为24厘米,相应的高度为10厘米。覆盖1080 m 2的地板需要多少个这样的瓷砖?
解决方案:
Given that,
Base of parallelogram = 24cm,
Height of parallelogram = 10cm,
Area of floor = 1080m2
As we know that,
Area of parallelogram = Base × Height
Area of 1 tiles = 24 × 10 = 240 cm2
As we know that 1m = 100cm,
So area will be 1080 m2 = 1080 × 100 × 100 cm2
Number of tiles required = Area of floor / Area of 1 tile
Number of tiles required = (1080 × 100 × 100) / (24 × 10) = 45000
Hence, Number of tiles required is 45000.
问题2。一个图是矩形ABCD的形式,在BC上有半圆,如图所示。如果AB = 60 m且BC = 28 m,请找到绘图区域。
解决方案:
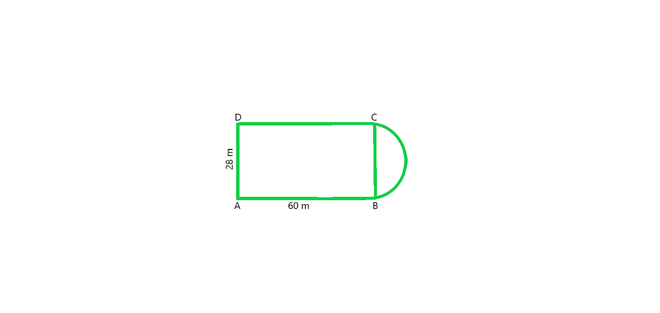
From figure, we conclude that, Area of the plot = Area of the rectangle + Area of semi-circle
Radius of semi-circle = BC/2 = 28/2 = 14m
As we know that Area of the Rectangular plot = Length × Breadth = 60 × 28 = 1680 m2
Area of the Semi-circular portion = πr2/2
= 1/2 × 22/7 × 14 × 14 = 308 m2
Hence, the total area of the plot = 1680 + 308 = 1988 m2
问题3.游乐场的形状为矩形,在其较小的侧面上有两个半圆作为直径,并添加到其外部。如果矩形的边分别为36 m和24.5 m,请找到操场的区域。 (取π = 22/7。)
解决方案:
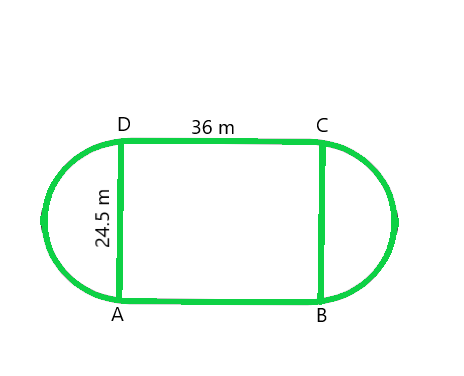
From figure, we conclude that, Area of the plot = Area of the Rectangle + 2 × area of one semi-circle
Radius of semi-circle = BC/2 = 24.5/2 = 12.25m (Given)
As we know that Area of the Rectangular plot = Length × Breadth = 36 × 24.5 = 882 m2
and Area of the Semi-circular portions = 2 × πr2/2
= 2 × 1/2 × 22/7 × 12.25 × 12.25 = 471.625 m2
Hence, the total Area of the plot = 882 + 471.625 = 1353.625 m2
问题4.一块矩形长20 m,宽15 m。从它的四个角开始,切掉了半径为3.5 m的象限。找到剩余部分的面积。
解决方案:
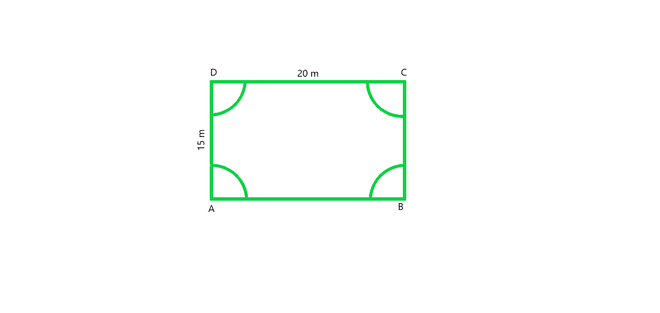
From figure, we conclude that, Area of the plot = Area of the rectangle – 4 × area of one quadrant
Radius of semi-circle = 3.5 m (Given)
Area of four quadrants = area of one circle (from figure)
Area of the plot = Length × Breadth – πr2
Hence, Area of the plot = 20 × 15 – (22/7 × 3.5 × 3.5) = 261.5 m2
问题5.运行轨迹的内周长(如图20.24所示)为400 m。每个笔直部分的长度为90 m,两端为半圆形。如果轨道到处都是14 m宽,请找到轨道的区域。另外,找到外部运行轨道的长度。
解决方案:
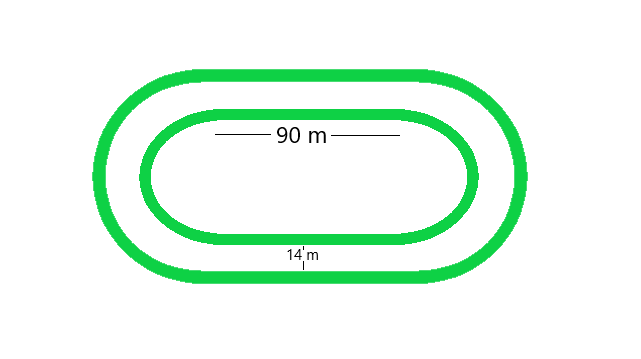
From figure, we conclude that, Perimeter of the inner track = 2 × Length of rectangle + perimeter of two semi-circular ends
Perimeter of the inner track = Length + Length + 2πr
400 = 90 + 90 + (2 × 22/7 × r)
(2 × 22/7 × r) = 400 – 180
(2 × 22/7 × r) = 220
44r = 220 × 7
44r = 1540
r = 1540/44 = 35
r = 35m
Hence, the radius of inner circle = 35 m
Now we have to calculate the radius of outer track
Radius of outer track = Radius of inner track + width of the track (from figure)
Radius of outer track = 35 + 14 = 49m (given)
Length of outer track = 2× Length of rectangle + perimeter of two outer semi-circular ends
Length of outer track = 2× 90 + 2πr
Length of outer track = 2× 90 + (2 × 22/7 × 49)
Length of outer track = 180 + 308 = 488
Hence, the Length of outer track = 488m
Area of inner track = Area of inner rectangle + Area of two inner semi-circles
Area of inner track = Length × Breadth + πr2
Area of inner track = 90 × 70 + (22/7 × 35 × 35)
Area of inner track = 6300 + 3850
Hence, the Area of inner track = 10150 m2
Area of outer track = Area of outer rectangle + Area of two outer semi-circles
Breadth of outer track = 35 + 35 +14 + 14 = 98 m
Area of outer track = length× breadth + πr2
Area of outer track = 90 × 98 + (22/7 × 49 × 49)
Area of outer track = 8820 + 7546
Hence, Area of outer track = 16366 m2
Now, we have to calculate the Area of path
Area of path = Area of outer track – Area of inner track
Area of path = 16366 – 10150 = 6216
Hence, Area of path is 6216 m2
问题6.找到以平方厘米为单位的图的面积,校正到小数点后一位。 (取π = 22/7)
解决方案:
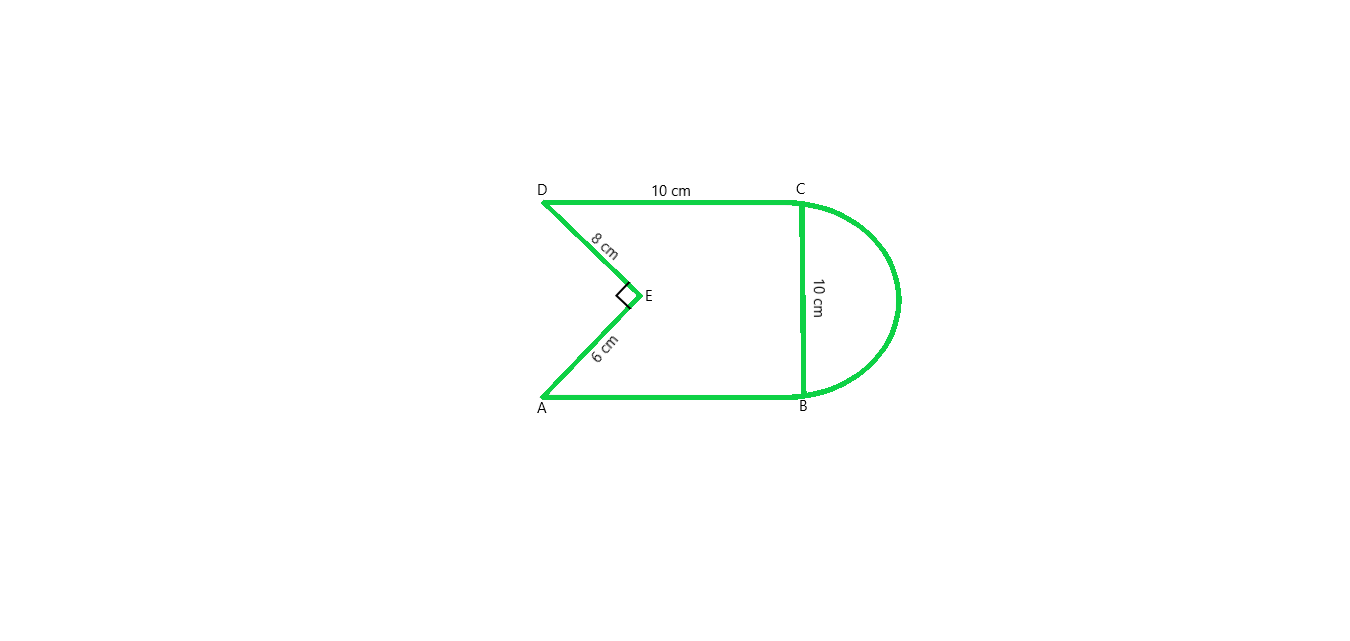
From figure we conclude that, Area of the Figure = Area of square + Area of semi-circle – Area of right angled triangle
Area of the Figure = side × side + πr2/2 – (1/2 × base × height)
put the values in formula and we get,
Area of the Figure = 10 × 10 + (1/2 × 22/7 × 5 × 5) – (1/2 × 8 × 6)
Area of the Figure = 100 + 39.28 – 24
Area of the Figure = 115.3
Hence, Area of the Figure = 115.3 cm2
问题7.公共汽车的车轮直径为90厘米,每分钟转315转。确定其速度(以公里/小时为单位)。 (取π = 22/7)
解决方案:
Given that,
Diameter of a wheel = 90 cm,
As we know that, Perimeter of wheel = πd
Perimeter of wheel = 22/7 × 90 = 282.857
Hence, the Perimeter of a wheel = 282.857 cm
Distance covered in 315 revolutions = 282.857× 315 = 89099.955 cm
As we know that 1 km = 100000 cm
So, The Distance covered = 89099.955/100000 = 0.89 km
Speed in km per hour = 0.89 × 60 = 53.4 km per hour.
问题8.菱形的面积为240厘米^ 2,对角线之一为16厘米。找到另一个对角线。
解决方案:
Given that,
Area of rhombus = 240 cm^2,
Diagonal = 16 cm.
As we know that,
Area of rhombus = 1/2 × d1 × d2
240 = 1/2 × 16 × d2
240 = 8 × d2
d2 = 240/8 = 30
Hence the other diagonal is 30 cm.
问题9.菱形的对角线是7.5厘米和12厘米。查找其区域。
解决方案:
Given that,
Diagonal(d1) = 7.5 cm,
Diagonal(d2) = 12 cm.
As we know that,
Area of rhombus = 1/2 × d1 × d2
Area of rhombus = 1/2 × 7.5 × 12
Area of rhombus = 6 × 7.5 = 45
Hence, Area of rhombus = 45 cm2
问题10.四边形形状的场的对角线为24 m,从其余相对顶点落在其上的垂线为8 m和13 m。查找字段的区域。
解决方案:
As we know that,
Area of quadrilateral = 1/2 × d1 × (p1 + p2)
Area of quadrilateral = 1/2 × 24 × (8 + 13)
Area of quadrilateral = 12 × 21 = 252
Hence, Area of quadrilateral is 252 cm2
问题11:找到菱形的侧面,菱形的侧面为6厘米,高度为4厘米。如果一条对角线的长度为8厘米,请找出另一条对角线的长度。
解决方案:
Given that,
Side of rhombus = 6 cm,
Altitude of rhombus = 4 cm.
As we know that rhombus is a parallelogram, therefore area of parallelogram = base × altitude
Therefore, Area of parallelogram = 6 × 4 = 24 cm2
Area of parallelogram = Area of rhombus
Area of rhombus = 1/2 × d1 × d2
24 = 1/2 × 8 × d2
24 = 4 × d2
d2 = 24/4 = 6
Hence, the length of other diagonal of rhombus is 6 cm.