第20章梯形和多边形区域-练习20.1 |套装1
问题12.建筑物的地板由3000块菱形瓷砖组成,每个对角线的长度分别为45厘米和30厘米。如果每平方米的成本为Rs,则找到抛光地板的总成本。 4,
解决方案:
As we know that,
Area of rhombus = 1/2 × d1 × d2
Area of rhombus = 1/2 × 45 × 30
Area of rhombus = 1350/2 = 675
Hence, Area of rhombus = 675 cm2
Area of one tile = 675 cm2 (Given)
Now, Area of 3000 tiles = 675× 3000 = 2025000 cm2
Area of tiles in m2 = 2025000/10000 = 202.5 m2
Hence, Total cost for polishing the floor = 202.5× 4 = Rs 810
问题13:一块矩形的草皮长112 m,宽78 m。它的侧面有2.5 m宽的砾石路。找出路径的面积以及以Rs建造路径的成本。每平方米4.50。
解决方案:
As we know that,
Outer area of rectangle = length × breadth
Outer area of rectangle = 112 × 78 = 8736 m2
Width of path = 2.5 m (Given)
Length of inner rectangle = 112 – (2.5 + 2.5) = 107 m
Breadth of inner rectangle = 78 – (2.5 + 2.5) = 73 m
Inner area of rectangle = length × breadth
Inner area of rectangle = 107 × 73 = 7811 m2
Now we will calculate Area of path,
Area of path = Outer area of rectangle – Inner area of rectangle
Area of path = 8736 – 7811 = 925 m2
Cost of construction for 1 m^2 = Rs 4.50 (Given)
Hence, Cost of construction for 925 m2 = 925 × 4.50 = Rs 4162.5
问题14:找到菱形的面积,菱形的每一边长20厘米,对角线之一是24厘米。
解决方案:
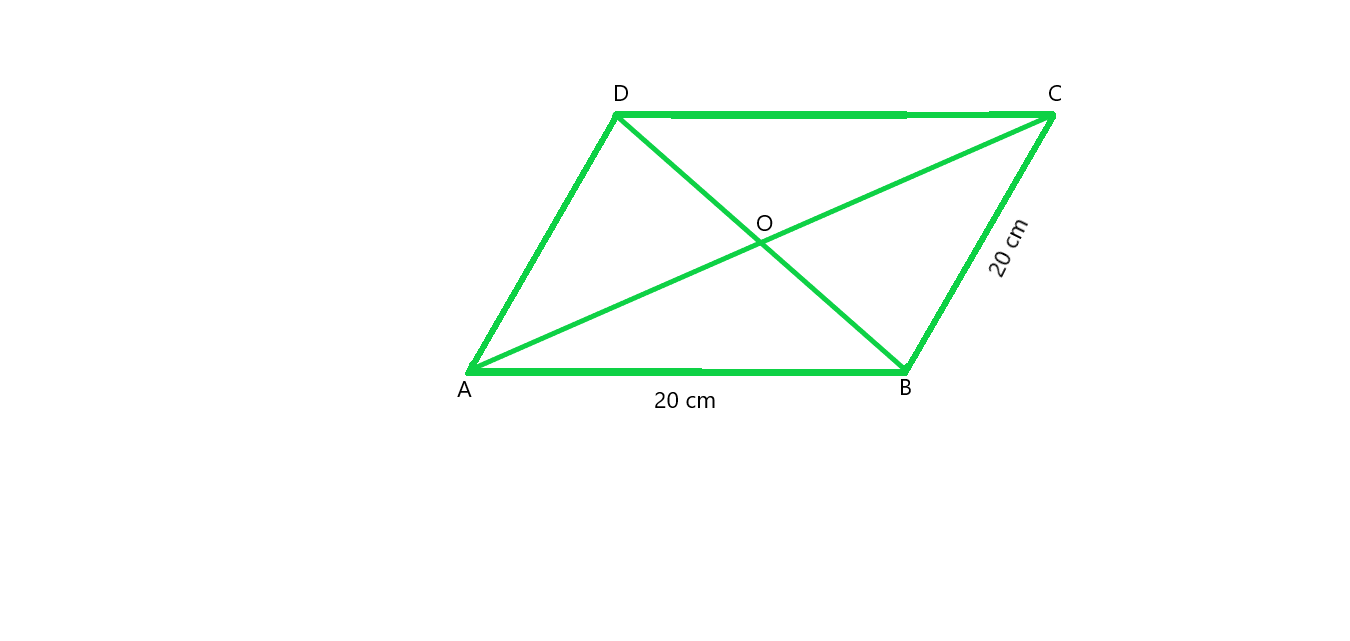
Given that,
Length of side of rhombus = 20 cm,
Length of one diagonal = 24 cm.
In ΔAOB,
Using Pythagoras theorem : AB2 = OA2 + OB2
202 = 122 + OB2
OB2 = 202 – 122
OB2 = 400 – 144
OB2 = 256
OB = 16
So, the length of the other diameter = 16 × 2 = 32 cm
As we know that Area of rhombus = 1/2 × d1 × d2
Area of rhombus = 1/2 × 24 × 32
Area of rhombus = 384 cm2
问题15:正方形场的边长为4 m。如果菱形的面积等于正方形场并且其对角线之一为2 m,则菱形的海拔高度是多少?
解决方案:
Given that,
Length of a side of a square = 4 m,
Area of square = (side)2,
Area of square = 4 × 4 = 16 m2
As we know that,
Area of square = Area of rhombus
Therefore, Area of rhombus = 16 m2
Area of rhombus = 1/2 × d1 × d2
16 = 1/2 × 2 × d2
16 = d2
The diagonal of rhombus = 16 m (Given)

In ΔAOB,
Using Pythagoras theorem
(AB)2 = (OA)2 + (OB)2
AB2 = 82 + 12
AB2 = 65
AB = √65
As we know that rhombus is a parallelogram, therefore area of parallelogram = base × altitude
Area of parallelogram = AB × DE
16 = √65 × DE
DE = 16/√65
Hence, Altitude of Rhombus = 16/√65 cm.
问题16:如果每边的长度为14厘米,高度为16厘米,则以菱形的形式找到视野区域。
解决方案:
Given that,
Side of rhombus = 14 cm,
Altitude of rhombus = 16 cm
As we know that rhombus is a parallelogram, therefore
Area of parallelogram = base × altitude
Area of parallelogram = 14 × 16 = 224 cm2
问题17:以每米60佩斯的价格围栏一个方形字段的成本为Rs。 1200.查找以每100平方米50派塞的速度收割田地的成本。
解决方案:
As we know that, Perimeter of square field = Cost of fencing / rate of fencing
Perimeter of square field = 1200/0.6 = 2000
Hence, Perimeter of square field = 2000 m
As we know that Perimeter of square = 4 × side
Side of square = Perimeter / 4 = 2000/4 = 500
So, the Side of square = 500 m
As we know that, Area of square = side2
Area of square = 500 × 500 = 250000 m2
Cost of reaping = (250000 × 0.5) / 100 = 1250
Hence, Cost of reaping the field is Rs 1250
问题18.作为交换,其中一个边长为84 m的正方形地块,一个男人想购买一个144 m长,面积与正方形地块相同的矩形地块。找到矩形图的宽度。
解决方案:
As we know that,
Area of square = side2
Area of square = 84 × 84 = 7056
Since, Area of square = Area of rectangle
7056 = 144 × width
Width = 7056/144 = 49
Hence, Width of rectangle = 49 m
问题19:菱形的面积为84 m 2 。如果其周长为40 m,则找到其海拔高度。
解决方案:
Given that,
Area of rhombus = 84 m2,
Perimeter = 40 m.
As we know that,
Perimeter of rhombus = 4 × side
Hence, Side of rhombus = Perimeter / 4 = 40/4 = 10
Side of rhombus = 10 m
Since rhombus is a parallelogram, therefore Area of parallelogram = base × altitude
84 = 10 × altitude
Altitude = 84/10 = 8.4
Hence, the Altitude of rhombus = 8.4 m
问题20:一个花园是菱形的,其侧面为30米,相应的高度为16 m。查找以Rs的比率对花园进行平整的成本。每平方米2个。
解决方案:
Given that,
Side of rhombus = 30 m,
Altitude of rhombus = 16 m.
As we know that, rhombus is a parallelogram, therefore Area of parallelogram = base × altitude
Area of parallelogram = 30 × 16 = 480 m2
Cost of levelling the garden = area × rate
Cost of levelling the garden = 480 × 2 = 960
Hence, the Cost of levelling the garden is Rs 960
问题21:菱形形式的场的每边长为64 m,高度为16 m。正方形区域的边与菱形区域相同的边是什么?
解决方案:
Given that,
Side of rhombus = 64 m,
Altitude of rhombus = 16 m,
As we know that rhombus is a parallelogram, hence Area of parallelogram = base × altitude
Area of parallelogram = 64 × 16 = 1024 m2
Since Area of rhombus = Area of square
Therefore, Area of square = side2
side2 = Area of square
Side of a square = √square
Side of square = √1024 = 32
Hence, Side of square = 32 m
问题22.菱形的面积等于其底边和相应高度分别为24.8厘米和16.5厘米的三角形的面积。如果菱形的对角线之一是22厘米,找到另一对角线的长度。
解决方案:
Given that,
Length of Base of Triangle = 24.8 cm,
Length of Altitude of Triangle= 16.5 cm.
As we know that Area of triangle = 1/2 × base × altitude
Area of triangle = 1/2 × 24.8 × 16.5 = 204.6
Hence Area of triangle = 204.6 cm
Since, Area of triangle = Area of rhombus
therefore Area of rhombus = 1/2 × d1 × d2
204.6 = 1/2 × 22 × d2
204.6 = 11 × d2
d2 = 204.6/11 = 18.6
Hence, the length of other diagonal is 18.6 cm.