8类RD Sharma解决方案–梯形和多边形的第20章区域-练习20.2 |套装2

第20章梯形和多边形区域-练习20.2 |套装1

问题11：运河的横截面是梯形。如果运河的顶部宽度为10 m，底部的宽度为6 m，且截面积为72 m ^2，则确定其深度。

解决方案：

Given:

Length of the parallel sides of the trapezium = 10m and 6m,

Area = 72 m²  

Assume that the distance between parallel sides of trapezium is x m

As we know that,

Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides

Now, put all the given values in this formula, and we get,

72 = 1/2 (10 + 6) × x

72 = 8 × x

x = 72/8 = 9

Hence, the depth is 9m.

问题12.梯形的面积为91 cm ² ，高度为7 cm。如果其中一个平行边比另一个平行边长8厘米，请找到两个平行边。

解决方案：

Given:

Assume that the length of one parallel side of trapezium = x m,

then, the length of other parallel side of trapezium = (x+8) m,

Area of trapezium = 91 cm²,

Height = 7 cm.

As we know that,

Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude

Now, put all the given values in this formula, and we get,

91 = 1/2 (x+x+8) × 7

91 = 1/2(2x+8) × 7

91 = (x+4) × 7

(x+4) = 91/7

x+4 = 13

x = 13 – 4 = 9

Hence, the length of one parallel side of trapezium = 9 cm

Therefore the length of other parallel side of trapezium = x+8 = 9+8 = 17 cm.

问题13.梯形的面积为384 cm ² 。它的平行边以3：5的比例，它们之间的垂直距离为12厘米。找出平行边各边的长度。

解决方案：

Given:

Assume that the length of one parallel side of trapezium = 3x m,

then the length of other parallel side of trapezium will 5x m,

Area of trapezium = 384 cm²,

Distance between the parallel sides of the trapezium = 12 cm.

As we know that,

Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides

Now, put all the given values in this formula, and we get,

384 = 1/2 (3x + 5x) × 12

384 = 1/2 (8x) × 12

4x = 384/12

4x = 32

x = 8

Hence, the length of one parallel side of trapezium = 3x = 3× 8 = 24 cm

and length of other parallel side of trapezium = 5x = 5× 8 = 40 cm.

问题14。莫汉想购买一个梯形的领域。它沿河的一侧是平行的，是沿道路的一侧的两倍。如果该区域的面积为10500 m ²且两个平行边之间的垂直距离为100 m，则求出沿河边的长度。

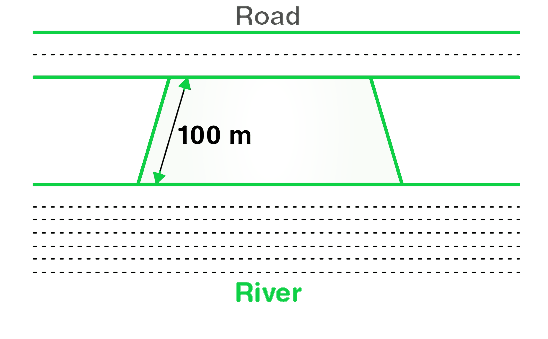
解决方案：

Given:

Assume that the length of side of trapezium shaped field along road = x m

and length of the other side of trapezium shaped field along road = 2x m,

Area of trapezium = 10500 cm²,

Distance between the parallel sides of the trapezium = 100 m.

As we know that,

Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides

Now, put all the given values in this formula, and we get,

10500 = 1/2 (x + 2x) × 100

10500 = 1/2 (3x) × 100

3x = 10500/50

3x = 210

x = 210/3 = 70

x = 70

Hence, the length of side of trapezium shaped field along road is 70 m

and length of other side of trapezium shaped field along road will 2x = 70× 2 = 140 m.

问题15.梯形的面积为1586 cm ² ，平行边之间的距离为26 cm。如果平行边之一为38厘米，找到另一边。

解决方案：

Given:

Let us assume that the length of other parallel side of trapezium = x cm 

and Length of one parallel side of trapezium = 38 cm,

Area of trapezium = 1586 cm²,

Distance between parallel sides = 26 cm.

As we know that,

Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides

Now, put all the given values in this formula, and we get,

1586 = 1/2 (x + 38) × 26

1586 = (x + 38) × 13

(x + 38) = 1586/13

x = 122 – 38

x = 84

Hence, the length of the other parallel side of the trapezium is 84 cm.

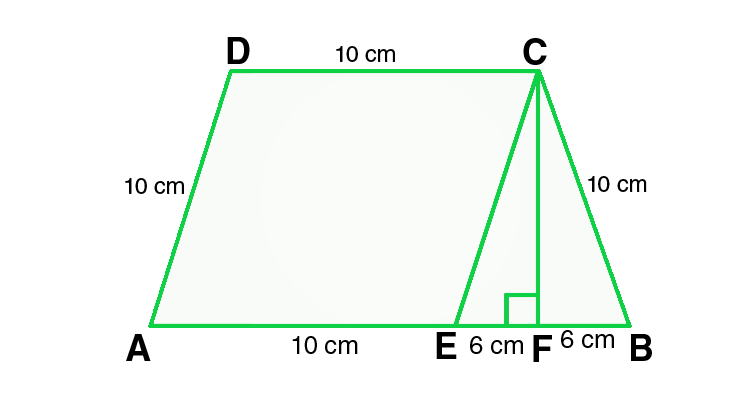
问题16.梯形的平行边分别为25 cm和13 cm。它的非平行边相等，每边10厘米，找出梯形的面积。

解决方案：

Given:

In ΔCEF,

CE = 10 cm and EF = 6cm

By using Pythagoras theorem,

CE² = CF² + EF²

CF² = CE² – EF²

CF² = 10² – 6²

CF² = 100 – 36

CF² = 64

CF = 8 cm

From the figure we conclude that,

Area of trapezium = Area of parallelogram AECD + Area of triangle CEF

= base × height + 1/2 (base × height)

= 13 × 8 + 1/2 (12 × 8) = 104 + 48 = 152

Hence, the area of trapezium is 152 cm².

问题17：找到梯形的面积，梯形的平行边分别为25 cm，13 cm和另一边分别为15 cm。

解决方案：

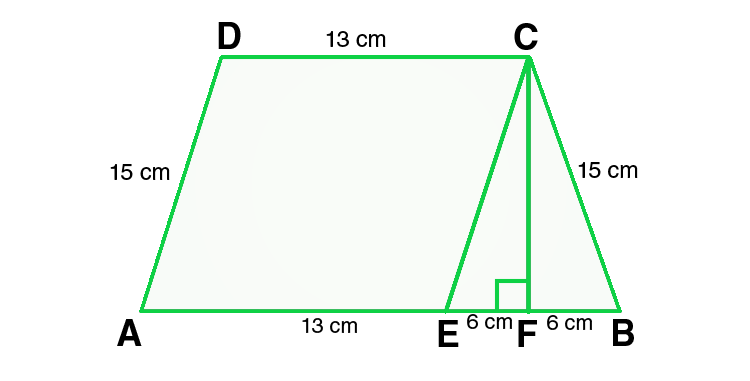
Given:

In ΔCEF,

CE = 10 cm and EF = 6cm

By using Pythagoras theorem,

CE² = CF² + EF²

CF² = CE² – EF²

CF² = 15² – 6²

CF² = 225 – 36

CF² = 189

CF = √189 = √ (9×21) = 3√21 cm                  

From the figure we conclude that,

Area of trapezium = Area of parallelogram AECD + Area of triangle CEF

= height + 1/2 (sum of parallel sides)

= 3√21 × 1/2 (25 + 13)                  

= 3√21 × 19 = 57√21

Hence, the area of trapezium is 57√21 cm².

问题18.如果梯形的面积为28 cm ²且其平行边之一为6 cm，则当梯形的高度为4 cm时找到另一平行边。

解决方案：

Given:

Let us assume that the length of other parallel side of trapezium = x cm,

Length of one parallel side of trapezium = 6 cm,

Area of trapezium = 28 cm²,

Length of altitude of trapezium = 4 cm.

As we know that,

Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides

Now, put all the given values in this formula, and we get,

28 = 1/2 (6 + x) × 4

28 = (6 + x) × 2

(6 + x) = 28/2

(6 + x) = 14

x = 14 – 6 = 8

Hence, the length of the other parallel side of trapezium is 8 cm.

问题19.在图中，在梯形图中绘制了一个平行四边形，平行四边形的面积为80 cm ² ，求出梯形的面积。

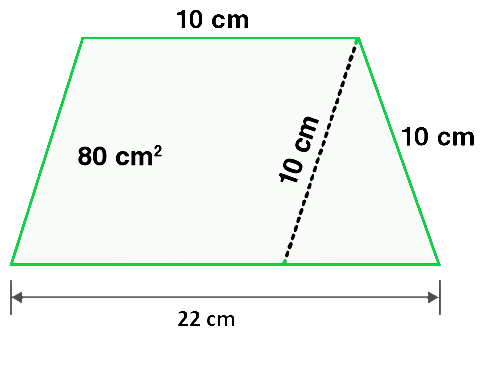
解决方案：

Given: 

In ΔCEF,

CE = 10 cm and EF = 6cm

By using Pythagoras theorem,

CE² = CF² + EF²

CF² = CE² – EF²

CF² = 10² – 6²

CF² = 100-36

CF² = 64

CF = 8 cm

Area of parallelogram = 80 cm^2            – (Given)

From the figure we conclude that,

Area of trapezium = Area of parallelogram AECD + Area of triangle CEF

So, area of trapezium = base × height + 1/2 (base × height)

Now, put all the given values in this formula, and we get,

= 10 × 8 + 1/2 (12 × 8)

= 80 + 48 = 128

Hence, the area of trapezium is 128 cm².

问题20.通过将其划分为正方形，矩形和梯形来找到图所示的区域。

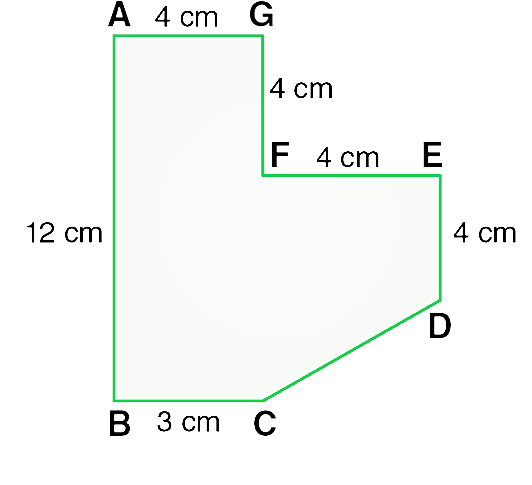
解决方案：

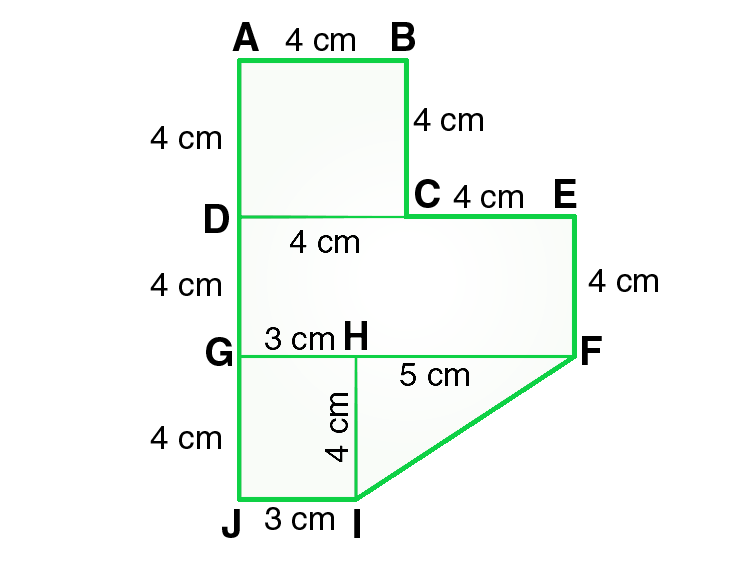
From the figure we conclude that,

Area of the given figure = Area of square ABCD + Area of rectangle DEFG +

                                            Area of rectangle GHIJ + Area of triangle FHI

Also,

Area of the given figure = side × side + length × breadth + 

                                             length × breadth + 1/2 × base × altitude

Now, put all the given values in this formula, and we get,

= 4×4 + 8×4 + 3×4 + 1/2×5×5 

= 16 + 32 + 12 + 10 

= 70

Hence, the area of given figure is 70 cm².