第11类RD Sharma解决方案–第23章直线-练习23.13

问题1：找出以下各对直线之间的夹角。

(i)3x + y + 12 = 0和x + 2y-1 = 0

解决方案：

Given equations of lines are,3x + y + 12 = 0, x + 2y -1 = 0

Letm₁ andm₂ be the slopes of these lines respectively.

By y = mx +c, we getm₁=-3 and m₂=-1/2

Let θ be the angle between the two lines,

By using formula $\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$

$\tan\theta=|\frac{(-3+\frac{1}{2})}{1+\frac{3}{2}}|$

⇒$|\frac{-5/2}{5/2}|$

⇒ 1

Therefore,$\theta=\tan^{-1}(1)$

The angles between the two lines is 45°.

(ii)3x-y + 5 = 0和x-3y + 1 = 0

解决方案：

Given equations of lines are 3x – y + 5 = 0, x – 3y +1 = 0

Let m₁ and m₂ be the slopes of these lines respectively.

By y = mx +c, we get m₁=3 and m₂=1/3

Let θ be the angle between the two lines,

We know that,$\tan\theta=|\frac{m_1-m_2}{1+m_1m_2}|$

$\tan\theta=|\frac{(3-\frac{1}{3})}{1+1}|$

⇒$\frac{4}{3}$

Therefore,$\theta=\tan^{-1}(\frac{4}{3})$

The angle between the two lines is$\tan^{-1}(\frac{4}{3})$

(iii)3x + 4y -7 = 0和4x-3y + 5 = 0

解决方案：

Given equations of lines are 3x + 4y – 7 = 0, 4x – 3y+5 = 0

Letm₁ andm₂ be the slopes of these lines respectively.

By y= mx +c, we get m₁ = $\frac{-3}{4}$and m₂ = $\frac{4}{3}$

Here, if we carefully observe, m₁m₂ = -1, which means

From the formula, $\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$denominator will become 0,

Therefore, $\tan\theta=\infty$,$\theta=\tan^{-1}(\infty)$

The angle between the two lines is 90°.

(iv)x-4y = 3和6x-y = 11

解决方案：

Given equations of lines are x – 4y =3, 6x – y =11

Letm₁ andm₂ be the slopes of these lines respectively.

By y = mx +c, we get, m₁=1/4 and m₂=6

Let θ be the angle between the two lines,

We know that,$\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$

⇒$|\frac{\frac{1}{4}-6}{1+\frac{3}{2}}|$

⇒$|\frac{\frac{-23}{4}}{\frac{5}{2}}|$

⇒$\frac{23}{10}$

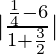
Therefore,$\theta=\tan^{-1}(\frac{23}{10})$

The angle between the two lines is$\tan^{-1}(\frac{23}{10})$

(v)(m ² -mn)y =(mn + n ² )x + n ³和(mn + m ² )y =(mn-n ² )x + m ³

解决方案：

Given two lines, letm₁ andm₂ be the slopes of these lines.

By y = mx +c, we getm₁ = $\frac{mn+m^2}{m^2-mn}$and m₂ = $\frac{mn-n^2}{m^2+mn}$

Let θ be the angle between two lines,

We know that$\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$

⇒ $|\frac{\frac{mn+n^2}{m^2-mn}-\frac{mn-n^2}{m^2+mn}}{1+\frac{(mn+n^2)(mn-n^2)}{{(m^2-nm)(m^2+mn)}}}|$

⇒$|\frac{(m^3n+m^2n^2+m^2n^2+m^3n-mn^3+m^2n^2+m^2n^2-mn^3)}{(m^4-n^4)}|$

⇒$\frac{4m^2n^2}{m^4-n^4}$

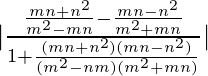
Therefore, Angle between two lines is$\tan^{-1}(\frac{4m^2n^2}{m^4-n^4})$.

问题2：找到线2x-y + 3 = 0和x + y + 2 = 0之间的锐角

解决方案：

Letm₁ andm₂ be the slopes of these two lines

By y = mx +c, we get m₁=2 and m₂=-1

Let θ be the angle between the two lines,

We know that,$\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$

⇒ $|\frac{2-(-1)}{(1-2)}|$

⇒ $|\frac{3}{(-1)}|$

Here we need acute angle,$\tan\theta$is positive if the angle is acute and negative if obtuse.

Therefore,$\theta=\tan^{-1}(3)$.

The acute angle between the two lines is$\tan^{-1}(3)$.

问题3：证明点(2，-1)，(0、2)，(2、3)和(4、0)是平行四边形的顶点坐标，并找到其对角线之间的角度。

解决方案：

Let the given points are A = (2,-1), B = (0, 2), C = (2, 3) and D = (4, 0) are coordinates of a parallelogram.

For these points to form a parallelogram, it is must that any pair of two lines formed by these points are parallel to each other.

So, Now lets find the slopes of lines AB, BC, CD, DA using formula$m =\frac{y_2 - y_1}{x_2-x_1}$

Slope of line $AB = \frac{-3}{2}$

Slope of line $BC =\frac{1}{2}$

Slope of line $CD = \frac{-3}{2}$

Slope of line $DA = \frac{1}{2}$

Since the lines AB parallel to CD and BC parallel to DA, the points form a parallelogram.

Now, Angle between the diagonals of parallelogram = Angle between the lines AC and BD.

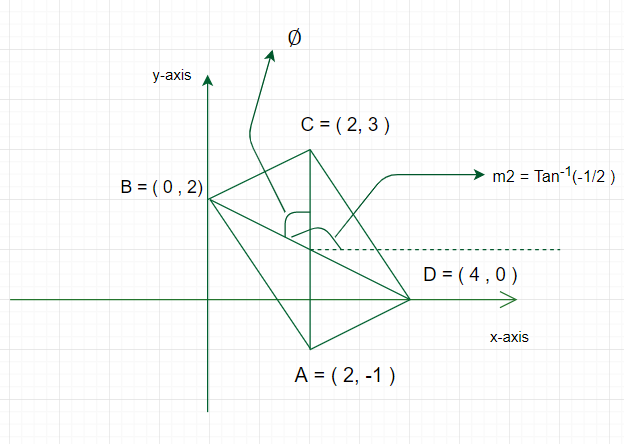
Letm₁ andm₂ be the slopes of these lines,

From the figure, the angle between diagonals$∅ = \tan^{-1}(\frac{-1}{2})-90°$

We know that$\tan^{-1}\theta+\tan^{-1}-\theta=\pi$

⇒ $∅=180°-\tan^{-1}(\frac{1}{2})-90°=90°-\tan^{-1}(\frac{1}{2})$

Therefore, The angle between the diagonals is $\frac{\pi}{2}-\tan^{-1}(\frac{1}{2})$

问题4：找到连接点(2，0)，(0，3)和直线x + y = 1之间的角度。

解决方案：

Let slope of line joining the points (2, 0) and (0, 3) is m₁ = -3/2

slope of line m₂ =-1

Let θ be the angle between the two lines,

We know that,$\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$

⇒$|\frac{\frac{-3}{2}+1}{1+\frac{3}{2}}|$

⇒$\frac{1}{5}$

Therefore, the acute angle between the line and the line joining the points is$\tan^{-1}(\frac{1}{5})$

问题5：如果θ是连接点(x1，y1)和(x2，y2)的直线在原点处所成的角度，则证明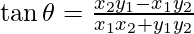$\tan\theta=\frac{x_2y_1-x_1y_2}{x_1x_2+y_1y_2}$和$\cos\theta=\frac{x_1x_2+y_1y_2}{\sqrt{(x_1^2+y_1^1)(x_2^2+y_2^2)}}$

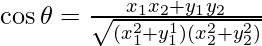
解决方案：

Let the points A = (x₁, y₁), B = (x₂, y₂) and origin O = (0, 0)

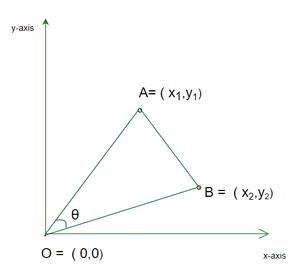
Slopes of lines joining OA and OB are m₁ = y₁/x₁ and m₂ = y₂/x₂

Let θ be the angle between the lines OA and OB.

We know that,$\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$

⇒$|\frac{(\frac{y_1}{x_1}-\frac{y_2}{x_2})}{(1+\frac{y_1y_2}{x_1x_2}}|$

Therefore,$\tan\theta=\frac{x_2y_1-x_1y_2}{x_1x_2+y_1y_2}$

By the formula$\sec^2\theta-\tan^2\theta=1$,we get$\cos\theta=\frac{1}{\sqrt{1+\tan^2\theta}}$

Substituting Tanθ from above equation, we get,

$\cos\theta=\frac{x_1x_2+y_1y_2}{\sqrt{(x_1^2+y_1^1)(x_2^2+y_2^2)}}$

Therefore, hence proved.

问题6：证明直线(a + b)x +(a – b)y = 2ab，(a – b)x +(a + b)y = 2ab和x + y = 0形成等腰三角形，其垂直角为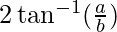$2\tan^{-1}(\frac{a}{b})$

解决方案：

Let m1, m2, m3 be the slopes of given lines respectively.

m₁ = $\frac{-(a+b)}{a-b}$, m₂ = $\frac{-(a-b)}{a+b}$and m₃ = -1

Let θ₁, θ₂, θ₃ be the angles between the lines

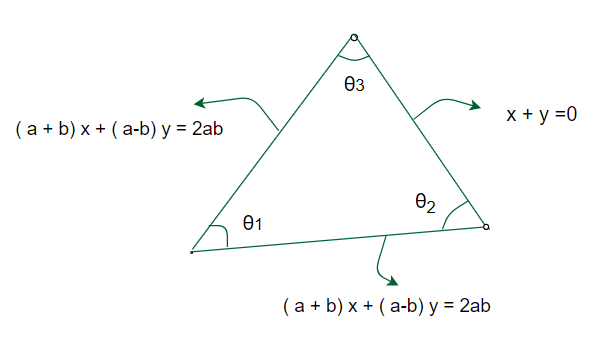
Now,$\tan\theta_1$=$|\frac{m_1-m_2}{1+m_1m_2}|$

⇒$|\frac{(a-b)^2-(a+b)^2}{2(a^2-b^2)}|$

⇒$|\frac{2ab}{a^2-b^2}|$⇒$|\frac{2\frac{a}{b}}{1-(\frac{a}{b})^2}|$

We know that$\tan2\theta=\frac{2\tan\theta}{1+\tan^2\theta}$, using this above equation

⇒ $\theta_1=2\tan^{-1}(\frac{a}{b})$

$\tan\theta_2$=$|\frac{m_2 - m_3}{1 + m_2m_3}|$

⇒$\frac{(-a + b +a + b)}{2a}⇒\frac{a}{b}$

⇒$\theta_2=\tan^{-1}(\frac{b}{a})$

$\tan\theta_3$=$|\frac{m_3 - m_1}{1 + m_3m_1}|$

⇒$\frac{(-a + b +a + b)}{2a}⇒\frac{a}{b}$

⇒$\theta_3=\tan^{-1}(\frac{b}{a})$

Here, angle θ₂ and θ₃ are equal, and θ₁ is the vertical angle

Therefore, the given lines forms Isosceles triangle with vertical angle$2\tan^{-1}(\frac{a}{b})$

问题7：求线之间的夹角x = a，乘+ c = 0

解决方案：

The given lines are in the form of x = constant and y=constant respectively

where x=c and y= -c/b

x = c line is parallel to y-axis as there is no y-coefficient

and $y=\frac{-c}{b}$is parallel to x-axis as there is no x-coefficient

Therefore, the Angle between the two lines is 90°

问题8：找出在轴上分别具有截距3、4和1、8的直线之间的角度的正切值。

解决方案：

Equation of line which have intercepts a, b on x and y-axis is$\frac{x}{a}+\frac{y}{b}=1$

Therefore, the line with intercepts 3,4 is$\frac{x}{3}+\frac{y}{4}=1$

and the line with intercepts 1, 8 is$\frac{x}{1}+\frac{y}{8}=1$

letm₁ and m₂ be the slopes of these lines,

m₁ = $\frac{-4}{3}$and m₂ = -8

Now, let θ be the angle between the lines,

$\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$

⇒ $|\frac{\frac{-4}{3}+8}{1+\frac{32}{3}}|$

⇒ $\frac{20}{35}$⇒ $\frac{4}{7}$

Therefore, The tangent of angle between the lines is 4/7

问题9：证明a ² x + ay + 1 = 0线垂直于x-ay = 1线

解决方案：

Letm₁ and m₂ be the slopes of given lines,m₁=-a andm₂=1/a

Here, if we carefully observe,m₁m₂=-1 ,which means

From the formula$\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$, denominator will become 0,

Therefore,$\tan\theta = \infty$, $\theta = \tan^{-1}(\infty)\ ⇒ 90°$.

The angle between the two lines is 90°, and they are perpendicular to each other.

Therefore, Hence proved.

问题10：显示线之间的角度切线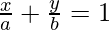$\frac{x}{a}+\frac{y}{b}=1$和$\frac{x}{a}-\frac{y}{b}=1$是$\frac{2ab}{a^2-b^2}$ 。

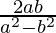解决方案：

Given lines,$\frac{x}{a} + \frac{y}{b} = 1$⇒ $bx + ay = ab$

$\frac{x}{a} - \frac{y}{b} = 1$⇒ $bx-ay = ab$

Let slopes of these lines arem₁ andm₂ respectively.

$m_1=\frac{-b}{a}$and$m_2=\frac{b}{a}$

Now, let θ be the angle between the lines,

$\tan\theta = |\frac{m_1-m_2}{1+m_1m_2}|$

⇒$|\frac{\frac{-b}{a}-\frac{b}{a}}{1 + \frac{b^2}{a^2}}|$

⇒$| \frac{2ab}{{a^2}-{b^2}}|$

Therefore, Tangent of angle between the lines is$\frac{2ab}{a^2-b^2}$

Hence, proved.