第11类RD Sharma解决方案–第23章直线-练习23.12 |套装2

问题11.找到连接点(a，b)和(a ₁ ，b ₁ )的线段的右等分线的方程。

解决方案：

Let us considered P(a, b) and Q(a₁, b₁) are the given points and O be the mid-point of line PQ.

So the coordinate O = ((a + a₁)/, (b + b₁)/2)

Slope of line PQ = $\frac{b_1-b}{a_1-a}$

And the slope of right bisector of AB(m’) = $-\frac{a_1-a}{b_1-b}$

The equation of required line is 

y – y₁ = m'(x – x₁)

$y-(\frac{b+b_1}{2})=\frac{a-a_1}{b-b_1}(x-\frac{a+a_1}{2})$

2x(a₁ – a) + 2y(b₁ – b) + a² + b² = a₁² + b₁² 

2x(a₁ – a) + 2y(b₁ – b) + (a² + b²) – (a₁² + b₁²) = 0

Hence, the equation of line is 2x(a₁ – a) + 2y(b₁ – b) + (a² + b²) – (a₁² + b₁²) = 0

问题12.找到关于线镜x + y – 5 = 0的点(2，1)的图像。

解决方案：

Let us considered P(2, 1) be the image of Q(a, b) are the given points and O be the mid-point of line PQ.

So the coordinate O = ((2 + a)/2, (1 + b)/2)

And O point lie on the line x + y – 5 = 0

(2 + a)/2 + (1 + b)/2 – 5 = 0

a + b = 7                 ………(1)

Here, x + y – 5 = 0 is perpendicular to PQ

So, (Slope of PQ) x (slope of AB) = -1

$-1\times (\frac{b-1}{a-2})=-1$

b – 1 = a – 2

b – a = -1           ………(2)

On solving eq(1) and (2), we get

a = 5 and b = 2

Hence, the image of (1, 2) in x + y – 5 = 0 is (4, 3)

问题13.如果相对于线镜的点(2，1)的像是(5，2)，请找到镜的方程。

解决方案：

Let us considered A(5, 2) be image of B(2, -1) and O be the mid point of AB

So the coordinate O = (7/2, 3/2)

Let us considered PQ be the mirror and line AB perpendicular to PQ

So, (Slope of PQ) x (slope of AB) = -1

(2 – 1/5 – 2) x (slope of AB) = -1

(slope of AB) = -3

So the equation of the mirror is 

y – 3/2 = -3(x – 7/2)

2y – 3 = -6x + 21

Hence, the equation of the mirror is 3x + y – 12 = 0

问题14.在平行于3x – 4y + 6 = 0的直线上找到方程，并通过连接点(2，3)和(4，-1)的中点。

解决方案：

It is given that A(2, 3) and B(4, -1) and O be the mid point of AB

So the coordinate O = (3, 1)

It is given that the equation to the straight line parallel to 3x – 4y + 6 = 0

So, 

y = 3x/4 + 3/2 

On comparing y = mx + c, we get

m = 3/4

Now put the value of m and (x₁, y₁) is eq(1), we get

The required equation of line is 

y – y₁ = m(x – x₁)    

y – 1 = 3/4(x – 3)

4y – 4 = 3x – 9

3x – 4y = 5

Hence, the equation of line is 3x – 4y = 5

问题15.证明2x – 3y + 1 = 0，x + y = 3、2x – 3y = 2和x + y = 4线形成平行四边形。

解决方案：

AS we know that in a parallelogram opposite sides are parallel and parallel sides have equal slope.

So, the slope of line 2x – 3y + 1 = 0

m₁ = 2/3             …….(1)

The slope of line x + y = 3 

m₂ = -1              …….(2)

The slope of line 2x – 3y – 2 = 0

m₃ = 2/3                 …….(3)

The slope of line x + y = 4

m₄ = -1                     …….(4)

From (1), (2), (3) and (4), we get 

We conclude that the opposite sides of ABCD have same slope 

Hence, the given quadrilateral is parallelogram. 

问题16.找到一条直线方程，该直线垂直于x / 4 + y / 6 = 1穿过与y轴相交的点。

解决方案：

Let us considered the required equation of line is 

y – y₁ = m(x – x₁)      ……….(1)

The required line is perpendicular to the given line x/4 + y/6 = 1

When x = 0

y/6 = 1

y = 6

So, the point (x₁, y₁) is (0, 6)

It is given that the required equation of line is perpendicular to the line x/4 + y/6 = 1

So,

(slope of required line) x (slope of given line) = -1

m1 = -1/(-6/4) = 4/6 = 2/3

Now put the value of m’ and (x₁, y₁) is eq(1), we get

(y – 6) = 2/3(x – 0)

2x – 3y = -18

2x – 3y + 18 = 0

Hence, the equation of line is 2x – 3y + 18 = 0

问题17.从原点到线y = mx + c的垂直线在点(-1，2)处相交。找到m和c的值。

解决方案：

Let us considered point O (0, 0) and P (-1, 2) and OP is perpendicular to the given line y = mx + c

So, (slope of OP) x (slope of line)=-1

$\frac{2-0}{-1-0}\times m=-1\\ m=\frac{-1\times -1}{2}=\frac{1}{2}$

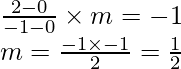
And point P lie on the line $y=\frac{1}{2}+c$ so,

2 = (1/2)(-1) + c

c = 2 + 1/2 = 5/2

Hence, the value of c = 5/2 and m = 1/2

问题18：找到连接点(3，4)和(-1，2)的线段的右等分线的方程。

解决方案：

Let us considered P(3, 4) and Q(-1, 2) are the given point and O be the mid point of AB

So, the coordinate O = (1, 3)

And the slope of line PQ is $\frac{2-4}{-1-3}=\frac{-2}{-4}=\frac{1}{2}$

The right bisector of PQ is -2

The equation of the required line is 

y – 3 = (-2)(x – 1)

y – 3 = -2x + 2

2x + y – 5 = 0

Hence, the required equation of line is 2x + y – 5 = 0

问题19.通过(h，3)和(4，1)的线与线7x – 9y – 19 = 0成直角相交。找出h的值。

解决方案：

Let us considered P (h, 3) and Q(4, 1) are the given points

Now the slope the line 7x – 9y – 19 = 0 is 7/9

It is given that line PQ is perpendicular to 7x – 9y – 19 = 0

so 

7/9 x (1 – 3)/(4 – h) = -1

9h = 22

h = 22/9

Hence, the value of h is 22/9

问题20.假设线为平面镜，找到关于线x + 3y = 7的点(3，8)的图像。

解决方案：

Let us considered A(5, 2) be image of B(a, b) and O be the mid point of AB

So, the coordinate of O = ((3 + a)/2, (8 + b)/2)

O point lies on line x + 3y = 7

So, (3 + a)/2 + 3 x ((8 + b)/2) = 7

a + 13b + 13 = 0   ……(1)

It is given that line AB is perpendicular to mirror PQ

So, slope of AB x slope of PQ = -1

(b – 8/a – 3) x -1/3 = -1

3a – b – 1 = 0   ……(2)

On solving eq(1) and (2), we get

a = -1, b = -4

Hence, the image is (-1, -4)