第11类RD Sharma解决方案–第23章直线–练习23.4

问题1.找到通过点(6，2)并具有-3斜率的直线方程。

解决方案：

We know (y – y₁) = m(x – x₁)

Here, m = Slope of line = -3

x₁ = 6, y₁ = 2

So, the equation of line is 

⇒ y – 2 = (-3)(x – 6)

⇒ y – 2 = -3x + 18

⇒ 3x + y – 20 = 0

问题2。找到通过(-2，3)并与x轴成45°角的直线的方程。

解决方案：

We know y – y₁ = m(x – x₁)

Here, m = Slope of line = tan 45° = 1

x₁ = -2, y₁ = 3

So, the equation of line is

⇒ y – 3 = 1(x – (-2))

⇒ y – 3 = x + 2

⇒ x – y + 5 = 0

问题3。找到直线方程，该方程将点(2、3)和(-5、8)的连接按比例3：4分开，并且也垂直于该方程。

解决方案：

Let the point at which the line divides the join of points (2, 3) and (-5, 8) in the ratio 3:4 be P(x₁, y₁)

P(x1, y1) = \frac{(4 × 2 – 5 × 3)}{(3 + 4)}, \frac{(4 × 3 + 3 × 8)}{(3+4)}

= (-1, 36/7)

Slope of the given points=(8-3)/(-5-2) =-5/7

Since, the required line is perpendicular to the line joining the given points.

Therefore, the slope of required line ‘m’ = 7/5 

Here, x₁ = -1, y₁ = 36/7 & m = 7/5

So, the equation of line is

⇒ y – 36/7 = 7/5(x – (-1))

⇒ y-36/7 = 7/5(x + 1)

⇒ 35y – 180 = 49x + 49

⇒ 49x + 35y + 229 = 0 is the required equation of straight line.

问题4.证明从(2，-1)和(6，5)的连接处的点(4，1)得出的垂线将其以5：8的比例进行划分。

解决方案：

Let PO be the perpendicular drawn from P(4,1) on the line joining A(2, -1) and B(6, 5)

 Let slope of PO be ‘m’ 

According to question 

m × Slope of AB = -1 

⇒ m × (5 + 1)/(6 – 2) = -1

⇒ m × 6/4 = -1

⇒ m = -4/6 = -2/3

Thus, the equation of line PO 

x1 = 4, y1 = 1 & m = -2/3

(y – 1) = -2/3(x – 4)

⇒ 3y – 3 = -2x + 8

⇒ 2x + 3y – 11 = 0 ——–(1)

Let O divide the line AB in the ratio of K:1

Then the coordinates of O are \frac{(6k + 2)}{(k + 1)}, \frac{(5k – 1)}{(k + 1)}

Since point O lies in the line AB

Therefore, it satisfies the equation (1)

$\frac{2(6k+2)}{(k+1)}+\frac{3(5k-1)}{(k+1)}-11=0$

⇒ 12k + 4 + 15k – 3 – 11(k + 1) = 0

⇒ 27k – 11k + 1 – 11 = 0

⇒ 16k = 10

⇒ k = 5/8 

Hence Proved

问题5。找到方程的三角形高度的方程，其角点为A(2，-2)，B(1，1)和C(-1，0)。

解决方案：

Let the altitudes be AE, BF and CD

Slope of AE × Slope of BC = -1                       [Since both lines are perpendicular to each other] 

Slope of AE = (-1) / Slope of BC

Slope of AE = 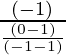$\frac{(-1)}{\frac{(0 - 1)}{(-1 - 1)}}$

= $-\frac{1}{\frac{1}{2}}$

= -2

Equation of the altitude AE 

y – (-2) = (-2)(x – 2)

⇒ y + 2 = -2x + 4

⇒ 2x + y – 2 = 0

Similarly,

Slope of BF × Slope of AC = -1

Slope of BF = $\frac{(-1)}{[\frac{(0 - (-2))}{(-1 - 2)}]}$

= $\frac{-1}{\frac{2}{-3}}$

= 3/2

Equation of the altitude BF

y – 1 = (3/2)(x – 1)

⇒ 2(y – 1) = 3x – 3

⇒ -3x + 2y – 2 + 3 = 0

⇒ 3x – 2y – 1 = 0

Slope of CD × Slope of AB = -1

Slope of CD= 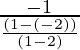$\frac{-1}{\frac{(1-(-2))}{(1-2)}}$

= $\frac{-1}{\frac{3}{-1}}$

= 1/3

Equation of the altitude CD

y – 0 = (1/3) (x – (-1))

⇒ 3y = x + 1

⇒ x – 3y + 1 = 0

问题6.找到连接点(3，4)和(-1，2)的线段的右等分线的方程。

解决方案：

Let the points of the line segment be A(3, 4) and B(-1, 2)

Let the right bisector meet at point ‘P’ on the line segment

Coordinates of point P = \frac{(3-1)}{2}, \frac{(4+2)}{2}          [Using the mid point formula]

= (1, 3)

Slope of AB = [(2 – 4) / (-1 – 3)]

=-2/-4

= 1/2

Slope of right bisector = $\frac{-1}{(\frac{1}{2})}$

= -2

Equation of the right bisector 

⇒ y – 3 = -2(x – 1)

⇒ y – 3 = -2x + 2

⇒ 2x + y – 5 = 0 is the required equation of the right bisector

问题7.找到通过点(3，-2)并与y轴正方向成60°角的直线方程。

解决方案：

Since the line is making an angle of 60° with the positive direction of y-axis i

t makes an angle of 30° with the positive direction of x-axis as shown in the diagram.

Slope of line ‘m’= tan 30° = 1/√3

Equation of straight line passing through (3, -2)

y – (-2) = 1/√3(x – 3)

⇒ √3(y + 2) = x – 3

⇒ √3y + 2√3 = x – 3

⇒ x – √3y – 3 – 2√3 = 0 is the required equation of straight line.

问题8.找到通过点(1，2)并与正弦为3/5的x轴正方向成角度的直线方程。

解决方案：

Given, sin θ = 3/5

tan θ = 3/√(25 – 9) = 3/4

Slope of the line m = 3/4

Equation of straight line passing through (1, 2)

y – 2 = 3/4(x – 1)

⇒ 4(y – 2) = 3x – 3

⇒ 4y – 8 = 3x – 3

⇒ 3x – 4y + 5 = 0 is the required equation of straight line.

问题9.找到穿过点(-3，5)并垂直于连接(2，5)和(-3，6)的线的方程。

解决方案：

Slope of the required equation ‘m’ = (-1) / [Slope of line joining (2, 5) and (-3, 6)]                 [Perpendicular to each other]

m =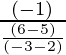$\frac{(-1)}{ \frac{(6-5)}{ (-3-2)} }$

m = $\frac{-1}{\frac{-1}{5}}$

m = 5                

Equation of straight line passing through (-3, 5)

y – 5 = 5(x – (-3))

⇒ y – 5 = 5x + 15

⇒ 5x – y + 20 = 0 is the required equation of straight line.

问题10.找到连接点A(1，0)和B(2，3)的线段的右等分线的方程。

解决方案：

Let the right bisector meet at point ‘P’ on the line segment

Coordinates of point P = [$\frac{(1+2)}{2}, \frac{(0+3)}{2}$ ]                   [Using the mid point formula]

= (3/2, 3/2)

Slope of AB = [(3 – 0)/(2 – 1)]

= 3/1 = 3

Slope of right bisector = -1/3

Equation of the right bisector  

⇒ y – 3/2 = -1/3(x – 3/2)

⇒ 3(y – 3/2) = -x + 3/2

⇒ x + 3y – 9/2 – 3/2 = 0

⇒ x + 3y – 6 = 0

⇒ x + 3y – 6 = 0 is the required equation of  the right bisector.

问题11。找到与x轴成角度π/ 3和2π/ 3的点(0，2)的线。另外，找到与它们平行的线，将它们在距原点以下2个单位的距离处切割y轴。

解决方案：

Given the line through the point (0, 2) making angles π/3 and 2π/3 with the x-axis

.Slope m1= tan π/3 = √3

Slope m2 = tan 2π/3 = -√3

Equation of the required lines

⇒ y – 2 = √3(x – 0) and y – 2 = -√3(x – 0) 

⇒ y – √3x – 2 = 0 and y + √3x – 2 = 0

Now, the equation of the line parallel to the line having slope m1 and y intercept c= -2

y = m1x + c 

⇒ y = √3x – 2

Similarly, the equation of the line parallel to the line having slope m2 and y intercept c = -2

y= m2x + c

⇒ y = -√3x – 2

问题12。求出从y轴截取截距5并相对于y轴相等倾斜的直线方程。

解决方案：

Given that the straight lines cut off an intercept 5 from the y-axis and are equally inclined to the axes.

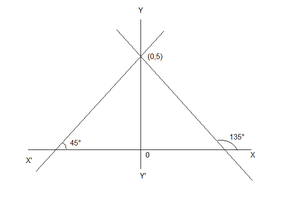
Slope of the two lines are m1= tan 45° =1 and m2 = tan 135° = -1

Equation of the required straight lines are 

y = m1x + c or y = m2 + c

⇒ y = x +5 or y = -x + 5

⇒ y = x +5 or y + x = 5            

问题13。找到直线方程，该方程在x轴的正方向上截取长度2，并且与y轴的正方向成135°角倾斜。

解决方案：

The required line which is inclined at an angle of 135° with the positive direction of y-axis makes an angle of 45° with the positive x-axis.

Slope of the required line m = tan 45° = -1

Equation of the required straight line with x-intercept c = 2 and m = -1

x = my + c

⇒ x = 1y + 2

⇒ x – y  – 2 = 0

问题14.找到斜率为m的通过(0，0)的线的方程。

解决方案：

Equation of line passing through (0, 0) with slope m is

y – 0 = m(x – 0)

⇒ y = mx

问题15。找到通过(2，2√3)并与x轴倾斜75°的直线的方程式。

解决方案：

Slope of the line m = tan 75° 

= tan (45° + 30°)

= (tan 45° + tan30°) /(1 – tan 45° tan30°)

= (1 + 1/√3)/(1 – 1/√3)

m = (√3 + 1)/(√3 – 1) = 2 + √3  

Equation of the required line passing through (2, 2√3) with slope of 2 + √3

y – 2√3 = (2 + √3)(x – 2)

⇒ y – 2√3  = (2 + √3)x – 4 – 2√3

⇒ (2 + √3)x – y – 4 = 0

问题16。找到通过(1，2)并与y轴成30°角的直线的方程式。

解决方案：

Let us considered an equation of line passing through points(x₁, y₁) which making an angle θ with x-axis.

(y – y₁) = tanθ(x – x₁)         -(1)

Given: Point = (1, 2), and angle = 30°(with y-axis)

So, angle with x-axis = 90° – 30° = 60°

Now put all these values in eq(1), we get

(y – 2) = tan60°(x – 1) 

(y – 2) = √3(x – 1) 

y – 2 = √3x – √3 

√3x – √3 – y + 2 = 0

√3x – y – √3  + 2 = 0