第11类RD Sharma解决方案–第23章直线-练习23.12 |套装1

问题1.找到一条穿过点(2，3)并与线3x – 4y + 5 = 0平行的线的方程。

解决方案：

Let us considered that the equation of line pass through point(2, 3) is 

y – y₁ = m(x – x₁)           ………(1)

It is given that the line is parallel to 3x – 4y + 5 = 0

So, the slope of 3x – 4y + 5 = 0

4y = 3x + 5

y = 3/4x + 5/4

On comparing y = mx + c, we get

m = 3/4

Now put the value of m and (x₁,y₁) is eq(1), we get

y – 3 = 3/4(x – 2)

4y – 12 = 3x – 6

3x – 4y = -12 + 6 

3x – 4y = -6

Hence, the equation of line is 3x – 4y + 6 = 0

问题2。找到通过(3，2)并垂直于x – 3y + 5 = 0的直线的方程。

解决方案：

Let us considered that the equation of line pass through point(2, 3) is 

y – y₁ = m(x – x₁)           ………(1)

Here (x₁, y₁) is (3, 2) and m is slope of line and slope -1/m is taken as lines are perpendicular

It is given that the line is perpendicular to 3x – 4y + 5 = 0

3y = x + 5

y = x/3 + 5/3

On comparing y = mx + c, we get

m = 1/3

Now put the value of m and (x₁,y₁) is eq(1), we get

$y-(-2)=-\frac{1}{\frac{1}{3}}(x-3)$

y + 2 = -3(x – 3) = -3x + 9

Hence, the equation of line is 3x + y = 7

问题3.找到连接点(1，3)和(3，1)的线的垂直平分线的方程。

解决方案：

Let us considered point A(1, 3) and B(3, 1)

As we know that any line that is perpendicular bisector which means line is perpendicular 

to the given line and one end point is the mid-point of that line.

So, the line AB has the mid-point

$x=\frac{x_1+x_2}{2},\space y=\frac{y_1+y_2}{2}$

(x₁,y₁) = $(\frac{1+3}{2},\frac{3+1}{2})$ = (2, 2)

Also slope of the line AB is 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{1-3}{3-1}=\frac{-2}{2}=-1$

Now we find the equation of perpendicular bisector:

$y-y_1=\frac{-1}{m}(x-x_1)$

y – 2 = 1(x – 2)

y – 2 = x – 2

y = x

问题4.求出顶点为A(1，4)，B(-3，2)和C(-5，-3)的∆ABC的高度方程。

解决方案：

Given that ABC is a triangle whose vertices are A(1, 4), B(-3, 2), and C(-5, -3)

Find: the equation of the altitudes of ∆ABC

So, let the perpendiculars of the triangle on the side AB, BC and AC are be CF, AD and FB 

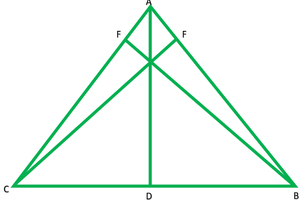
The slope of the side AB = $\frac{4-2}{1+3}=\frac{2}{4}=\frac{1}{2}$

Slope of CF = $\frac{1}{\frac{1}{2}}$= -2           

So, the equation of side CF is 

y – y₁ = m(x – x₁)

y + 3 = -2(x + 5)      

y + 3 = -2x – 10

y = -2x – 13

The slope of the side BC = $\frac{2+3}{-3+5}=\frac{5}{2}$

And the slope of AD = $-\frac{1}{\frac{5}{2}}=-\frac{2}{5}$

So, the equation of side AD is 

y – y₁ = m(x – x₁)

y – 4 = $-\frac{2}{5}$(x – 1)

5y – 20 = -2x + 2

5y = -2x – 22

The slope of the side AC = $\frac{4+3}{1+5}=\frac{7}{6}$

And the slope of EB = $-\frac{1}{\frac{7}{6}}=-\frac{6}{7}$

So, the equation of side FB is 

y – y₁ = m(x – x₁)

y – 2 = -6/7(x + 3)

7y – 14 = -6x – 18

7y = -6x – 4

Hence, the equations of the altitudes of ∆ABC are 

AD = 2x + 5y + 22 = 0

CF = 2x + y + 13 = 0

FB = 6x + 7y + 4 = 0

问题5.找到一条垂直于√3x– y + 5 = 0的直线的方程，该方程将y轴为负的方向截断4个单位的截距。

解决方案：

Let us considered the required equation of line is 

y – y₁ = m'(x – x₁)      ……….(1)

So, point (x₁, y₁) = (0, -4)

It is given that the line is perpendicular to line 3x – y + 5 = 0

So, the slope of 3x – y + 5 = 0 

y = 3x + 5

On comparing y = mx + c, we get

m = √3

As we know that the line is perpendicular to the line 3x – y + 5 = 0

So, the slope is m’ = -1/m = -1/√3

Now put the value of m’ and (x₁, y₁) is eq(1), we get

y – (-4) = -1/√3(x – 0) 

y + 4 = -x/√3

x + √3y + 4√3 = 0

问题6.如果相对于线镜的点(2，1)的图像是(5，2)，请找到该镜的方程。

解决方案：

Let us considered the image of point Q(2, 1) is R(5, 2) and O is the mid point of line QR

So, the coordinate of O is ((2 + 5)/2, (1 + 2)/2) = (7/2, 3/2)

Now let us considered AB be the mirror and line QR is perpendicular to AB

So, m1 x m2 = -1

Here, m1 is the slope of AB and m2 is the slope of CD

$(\frac{2-1}{5-2})$ x m2 = -1

1/3 x m2 = -1

m2 = -3

So the slope of CD is -3

Now we find the equation of CD

y – y₁ = m(x – x₁)

y -(3/2) = (-3)(x – 7/2)

(2y -3)/2 = -3x +21/2

2y – 3 = -6x + 21

6x + 2y = 24

3x + y = 12

Hence, the equation of the mirror is 3x + y – 12 =0

问题7.找到通过点(α，β)并垂直于直线lx + my + n = 0的直线方程。

解决方案：

Let us considered the required equation of line is 

y – y₁ = m'(x – x₁)      ……….(1)

So, point (x₁, y₁) = (α, β)

It is given that the line is perpendicular to the line lx + my + n = 0

So, the slope of line lx + my + n = 0 is

y = -lx/m – n/m 

On comparing y = mx + c, we get

m = -l/m

As we know that the line is perpendicular to the line lx + my + n = 0

So, the slope is m’ = -1/m = m/l

Now put the value of m’ and (x₁, y₁) is eq(1), we get

y – β = m/l(x – α)

ly + mx = ma + lβ

m(x – a) = l(y – β)

Hence, the equation of the straight line is m(x – a) = l(y – β)

问题8.找到垂直于2x – 3y = 5的直线方程，并在x轴的正方向上截取截距1。

解决方案：

Let us considered the required equation of line is 

y – y₁ = m'(x – x₁)      ……….(1)

So, point (x₁, y₁) = (1, 0)

It is given that the line is perpendicular to the line 2x – 3y = 5

So, the slope of line 2x – 3y = 5 is

y = -2x/3 + 5/3 

On comparing y = mx + c, we get

m = -2/3

As we know that the line is perpendicular to the line lx + my + n = 0

So, the slope is m’ = -1/m = 3/2

Now put the value of m’ and (x₁, y₁) is eq(1), we get

y – y₁ = m(x – x₁) 

y – 0 = 2/3(x – 1)

y = -3/2(x – 1)

2y = -3x + 3

Hence, the equation of the required line is 3x + 2y – 3 = 0

问题9.找到垂直于5x – 2y = 8的直线的方程，该方程通过连接(2，3)和(4，5)的线段的中点。

解决方案：

Let us considered point A(2, 3) and (4, 5) and O be the mid point of AB

so the coordinates of O = ((2 + 4)/2, (3 + 5)/ 2) = (3, 4)

Let us considered the required equation of line is 

y – y₁ = m'(x – x₁)      ……….(1)

Here (x₁,y₁) is (3, 4)

It is given that the line is perpendicular to the line 5x – 2y = 8

So, the slope of line 5x – 2y = 8 is

y = 5x/2 – 4

On comparing y = mx + c, we get

m = 5/2

As we know that the line is perpendicular to the line 5x – 2y = 8

So, the slope is m’ = -1/m = -2/5

Putting m and (x₁,y₁) in (1), we get

y – 4 = (-2/5)(x – 3)

5y + 2x = 26

2x + 5y – 26 = 0

Hence, the equation of the required line is 2x + 5y – 26 = 0

问题10。求出y轴截距等于4/3且垂直于3x – 4y + 11 = 0的直线方程。

解决方案：

Let us considered the required equation of line is 

y – y₁ = m'(x – x₁)      ……….(1)

Here (x₁, y₁) is (0, 4/3)

It is given that the line is perpendicular to the line 3x – 4y + 11 = 0.

So, the slope of line 3x – 4y + 11 = 0 is

y = 3x/4 – 11/4

On comparing y = mx + c, we get

m = 3/4

As we know that the line is perpendicular to the line 3x – 4y + 11 = 0.

So, the slope is m’ = -1/m = -4/3

Putting m and (x₁, y₁) in (1), we get

y – 4/3 = (-4/3)(x – 0)

4x + 3y – 4 = 0

Hence, the equation of the required line is 4x + 3y – 4 = 0