11类NCERT解决方案-第7章排列和组合–练习7.4

问题1.如果ⁿ C ₈ = ⁿ C ₂ ，则找到ⁿ C ₂ ^。

解决方案：

We know that, ⁿC_r=ⁿC_(n-r)

For the given question, r=8 and n-r=2

Hence, n=r+(n-r)=8+2=10

OR

Using formula (1),

ⁿC₈=ⁿC_(n-r)

$\frac{n!}{8!(n-8)!}=\frac{n!}{2!(n-2)!} \\i.e. \frac{n}{8(n-8)}=\frac{n}{2(n-2)}$

8(n-8)=2(n-2) 

4(n-8)=n-2 

4n-32=n-2 

3n=30 

n=10

As n=10, 

¹⁰C₂ = $\frac{10!}{2!8!}=\frac{10*9}{2} =45$

问题2.确定n是否(i) ²ⁿ C ₃ ： ⁿ C ₃ = 12：1(ii) ²ⁿ C ₃ ： ⁿ C ₃ = 11：1

解决方案：

i) 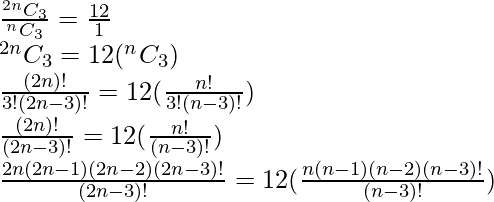$\frac {^{2n}C_3 }{^{n}C_3}=\frac{12}{1} \\\,^{2n}C_3 =12(^{n}C_3) \\\frac{(2n)!}{3!(2n-3)!}=12(\frac{n!}{3!(n-3)!}) \\\frac{(2n)!}{(2n-3)!}=12(\frac{n!}{(n-3)!}) \\\frac{2n(2n-1)(2n-2)(2n-3)!}{(2n-3)!}=12(\frac{n(n-1)(n-2)(n-3)!}{(n-3)!})$

2n(2n-1)(2n-2)=12n(n-1)(n-2) 

(2n-1)2(n-1)=6(n-1)(n-2) 

2n-1=3(n-2) 

2n-1=3n-6 

n=5

ii) $\frac {^{2n}C_3 }{^{n}C_3}=\frac{11}{1} \\\,^{2n}C_3 =11(^{n}C_3) \\\frac{(2n)!}{3!(2n-3)!}=11(\frac{n!}{3!(n-3)!}) \\\frac{(2n)!}{(2n-3)!}=11(\frac{n!}{(n-3)!}) \\\frac{2n(2n-1)(2n-2)(2n-3)!}{(2n-3)!}=11(\frac{n(n-1)(n-2)(n-3)!}{(n-3)!})$

2n(2n-1)(2n-2)=11n(n-1)(n-2) 

2(2n-1)2(n-1)=11(n-1)(n-2) 

4(2n-1)=11(n-2) 

8n-4=11n-22 

3n=18 

n=6

问题3.圆上21个点可以画多少个和弦?

解决方案：

Chord of a circle is made by using any two points on a circle. So, we have to select any 2 points from 21 to draw a chord. 

Hence, chords that can be drawn through 21 points on a circle

= ²¹C₂ =$\frac{21!}{2!19!}=\frac{21*20}{2}$= 210

问题4.从5个男孩和4个女孩中选择一个由3个男孩和3个女孩组成的团队吗?

解决方案：

We have to select 3 boys from 5 boys and 3 girls from 4 girls to make a team. 

Number of ways to select 3 boys = ⁵C₃= $\frac{5!}{3!2!}$ = 10

Number of ways to select 3 girls = ⁴C₃ = $\frac{4!}{3!1!}$ = 4

Hence, Number of ways to make a required team = 10*4 = 40 

问题5.如果每种选择都由每种颜色的3个球组成，则找出从6个红色球，5个白色球和5个蓝色球中选择9个球的方法数量。

解决方案：

We have to select 3 balls from 6 red balls, 3 from 5 white balls and 3 from 5 blue balls.

Number of ways to select 3 balls from 6 red balls= ⁶C₃ = $\frac{6!}{3!3!}$ =20

Number of ways to select 3 balls from 6 red balls= ⁵C₃ = $\frac{5!}{3!2!}$ =10

Number of ways to select 3 balls from 6 red balls= ⁵C₃ =$\frac{5!}{3!2!}$ =10

Number of ways to select 9 balls in required way=20*10*10=2000

问题6.如果每组中只有一张王牌，则从52张牌中确定5张卡组合的数量。

解决方案：

We have to select 5 cards from 52 cards. If there is exactly one ace in each combination, then 

1) we have to select 1 Ace card from 4 ace cards

2) we have to select 5-1=4 cards from remaining 52-4=48 cards

So, 1) Number of ways to select Ace card= ⁴C₁ = $\frac{4!}{1!3!}$= 4

2) Number of ways to select remaining 4 cards

= ⁴⁸C₄ =$\frac{48!}{4!44!}=\frac{48*47*46*45}{4*3*2}=194580$

And, hence required total number of 5 card combinations=4*194580=778320.

问题7.从17个球员中选择一个11人的板球队，如果每个11人的板球队必须恰好包括4个保龄球，那么只有5个球员可以打保龄球?

解决方案：

We have to select 11 players from 17 players. Among 17 players, 5 are bowlers. So, if there are exactly 4 bowlers to be selected in team of 11 players, then

1) Number of ways to select 4 bowlers from 5=⁵C₄=$\frac{5!}{4!1!}$=5

2) Number of ways to select remaining 11-4=7 players from 17-5=12 players

= ¹²C₇ = $\frac{12!}{7!5!}$=792

And, hence required total number of ways to select a cricket team=792*5=3960

问题8.一个袋子包含5个黑色和6个红色的球。确定可以选择2个黑色和3个红色球的方式数量。

解决方案：

We have to select 2 balls from 5 black balls and 3 balls from 6 red balls.

Number of ways to select 2 black balls= ⁵C₂ =$\frac{5!}{2!3!}$ =10

Number of ways to select 3 red balls = ⁶C₃ = $\frac{6!}{3!3!}$ =20

Hence, Number of ways to make a required team = 10*20=200

问题9.如果每个学生有9门课程并且必修2门特定课程，则学生可以选择多少种5门课程?

解决方案：

A student choose 5 courses. Among these 5 courses 2 specific courses are compulsory. Hence, student have to choose 5-2=3 courses from available 9-2=7 courses.

Hence, Number of ways a student can choose a programmer of 5 courses= ⁷C₃ * ²C₂ = $\frac{7!}{3!4!}*\frac{2!}{2!0!}$ =35*1 =35