第12类RD Sharma解决方案–第23章，矢量代数–练习23.3

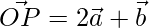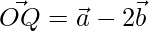问题1  求出点R的位置向量，该点用位置向量将连接两个点P和Q的线分开$\vec{OP}=2\vec{a}+\vec{b}$和$\vec{OQ}=\vec{a}-2\vec{b}$内部和外部分别以1：2的比例。

解决方案：

The point R divides the line joining points P and Q in the ratio 1:2 internally.

The position vector of R =  $\frac{\vec{a}-2\vec{b}+2(2\vec{a}+\vec{b})}{1+2}$= $\frac{5\vec{a}}{3}$

Point R divides the line joining P and Q in the ratio 1:2 externally.

The position vector of R = $\frac{\vec{a}-2\vec{b}-2(2\vec{a}+\vec{b})}{1-2}$

= $\frac{-3\vec{a}-4\vec{b}}{-1}$

= $3\vec{a}+4\vec{b}$

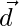问题2。 $\vec{a},\vec{b},\vec{c}$和$\vec{d}$是四个不同点A，B，C，D的位置向量。 $\vec{b}-\vec{a}=\vec{c}-\vec{d}$然后证明ABCD是平行四边形。

解决方案：

Given that  are the position vectors of the four distinct points A, B, C, D 

such that $\vec{b}-\vec{a} = \vec{c}-\vec{d}$

Given that, 

$\vec{b}-\vec{a} = \vec{c}-\vec{d}$

$\vec{AB} = \vec{CD}$

So, AB is parallel and equal to DC 

Hence, ABCD is a parallelogram.

问题3。 如果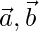$\vec{a},\vec{b}$分别是A，B的位置向量，找到在AB中产生的点C的位置向量，使得AC = 3AB，在BA中产生点D的位置向量，使得BD = 2BA。

解决方案：

Given that $\vec{a},\vec{b}$are the position vector of A and B

Let C be a point in AB produced such that AC = 3AB.

From the given data we can say that point C divides the line AB in

Ratio 3:2 externally. So, the position vector of point C can be written as

$\vec{c} = \frac{ m\vec{b}-n\vec{a}}{m-n}$

= $\frac{3\vec{b}-2\vec{a}}{3-2}$

=  $3\vec{b}-2\vec{a}$

D be a point in BA produced such that BD = 2BA

It is clear that point D divides the line in 1:2 externally. 

Then the position vector $\vec{d}$ can be written as

$\vec{d} = \frac{m\vec{a}-n{b}}{m-n}$

=  $\frac{2\vec{a}-\vec{b}}{2-1}$

$\vec{d} = 2\vec{a}-\vec{b}$

Hence  $\vec{c} =3\vec{b}-2\vec{a}$and  $\vec{d} = 2\vec{a}-\vec{b}$

问题4。 显示带有位置矢量的四个点A，B，C，D $\vec{a},\vec{b},\vec{c}$和$\vec{d}$分别这样$3\vec{a}-2\vec{b}+5\vec{c}-6\vec{d} =\vec{0}$是共面的。另外，找到线AC和BD的交点的位置矢量。

解决方案：

Given that $3\vec{a}-2\vec{b}+5\vec{c}-6\vec{d} =\vec{0}$

$3\vec{a}+5\vec{c} = 2\vec{b}+6\vec{d}$

Sum of the coefficients on both sides of the given equation is 8

so, divide the equation by 8 on both the sides

$\frac{3\vec{a}+5\vec{c}}{8} = \frac{2\vec{b}+6\vec{d}}{8}$

$\frac{3\vec{a}+5\vec{c}}{3+5} = \frac{2\vec{b}+6\vec{d}}{2+6}$

It is clear that the position vector of a point P dividing Ac in the 

Ratio 3:5 is same as that of point P diving BD in the ratio 2:6.

Point P is common to AC and BD. Hence, P is the point of intersection of AC and BD.

Therefore, A, B, C and D are coplanar.

The position vector of point P can be written as 

$\frac{3\vec{a}+5\vec{c}}{8}$ or $\frac{2\vec{b}+6\vec{d}}{8}$

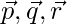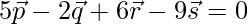问题5： 证明带有位置矢量的四个点P，Q，R，S $\vec{p},\vec{q},\vec{r}$和$\vec{s}$分别这样$5\vec{p}-2\vec{q}+6\vec{r}-9\vec{s} = 0$是共面的。此外，找到直线PR和QS的交点的位置向量。

解决方案：

Given that $5\vec{p}-2\vec{q}+6\vec{r}-9\vec{s} = 0$

Here  $\vec{p}, \vec{q}, \vec{r},$and $\vec{s}$

are the position vectors of point P, Q, R, S

$5\vec{p}+6\vec{r} = 2\vec{q}+9\vec{s}$          -(1)

Sum of the coefficients on both the sides of the equation (1) is 11. 

So divide the equation (1) by 11 on both sides.

$\frac{5\vec{p}+6\vec{r}}{11} = \frac{2\vec{q}+9\vec{s}}{11}$

$\frac{5\vec{p}+6\vec{r}}{5+6} = \frac{2\vec{q}+9\vec{s}}{2+9}$

It shows that position vector of a point A dividing PR in the ratio of 6:5 and

 QS in the ratio 9:2. So A is the common point to PR and QS.

Therefore, P, Q, R and S are coplanar.

The position vector of point A is given by 

$\frac{5\vec{p}+6\vec{q}}{11}$or $\frac{2\vec{q}+9\vec{s}}{11}$

问题6： 三角形ABC的顶点A，B，C分别具有位置矢量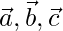$\vec{a},\vec{b},\vec{c}$相对于给定的原点O。表明点D的等分线$\angle{A}$遇见BC有位置向量$\vec{d}=\frac{\beta\vec{b}+\gamma\vec{c}}{\beta+\gamma}$在哪里$\beta=|\vec{c}-\vec{a}| = \gamma=|\vec{b}-\vec{a}|$ 。因此推断出中心I具有位置向量$\frac{\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}}{\alpha+\beta+\gamma}$在哪里$\alpha = |\vec{b}-\vec{c}|$

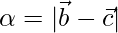
解决方案：

Let ABC be a triangle and the position vectors of A, B, C with respect to some origin say O be 

Let D be the point on BC where the bisector of $\angle{A}$ meets.

$\vec{d}$ be the position vector of D which divides BC internally in the ratio $\beta$ 

and $\gamma$where $\beta = |\vec{AC}| and \gamma = {\vec{b}-\vec{a}}$ 

Thus, $\beta=|\vec{c}-\vec{a}| and \gamma=|\vec{b}-\vec{a}|$

Therefore, by section formula, the position vector of D is given by

 $\vec{OD} = \frac{\beta\vec{b}+\gamma\vec{c}}{\beta+\gamma}$

Let $\alpha = |\vec{b}-\vec{c}|$

Incentre is the concurrent point of angle bisectors.

Thus, Incentre divides the line AD in the ratio $\alpha:\beta+\gamma$ and 

the position vector of incentre is equal to

$\frac{\alpha\vec{a}+\frac{\beta\vec{b}+\gamma\vec{c}}{(\beta+\gamma)}*(\beta+\gamma)}{\alpha+\beta+\gamma} = \frac{\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}}{\alpha+\beta+\gamma}$