第 12 类 RD Sharma 解决方案 – 第 23 章向量代数 – 练习 23.4
问题1.若O为空间中的一点,ABC为三角形,D、E、F分别为三角形的边BC、CA、AB的中点,证明:
解决方案:
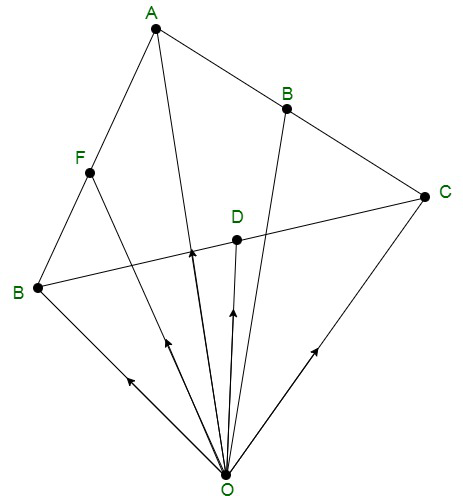
In the △ABC, D, E, F are the mid points of the sides of BC, CA and AB and O is any point in space.
Let us considered ![]() be the position vector of point A, B, C, D, E, F with respect to O.
be the position vector of point A, B, C, D, E, F with respect to O.
Therefore, 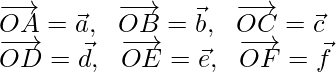
So, according to the mid-point formula
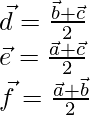
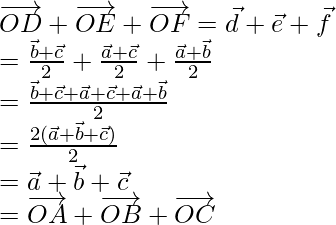
Hence, proved
![]()
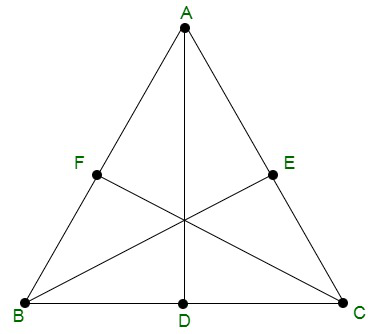
问题 2. 证明由顶点指向的三角形的中线确定的三个向量之和为零。
解决方案:
Let us considered ABC is triangle, so the position vector of A, B and C are ![]()
Hence, AD, BE, CF are medium, so, D, E and F are mid points of line BC, AC, and AB.
Now, using mid point formula we get
Position vector of D = ![]()
Position vector of E = ![]()
Position vector of F = ![]()
Now, add all the three median
![]()
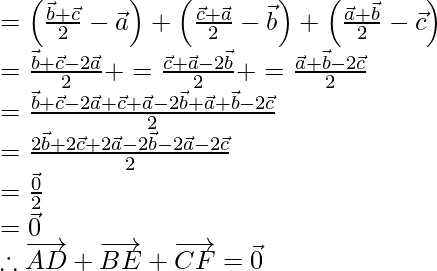
Hence, proved that the sum of the three vectors determined by the medians
of a triangle directed from the vertices is zero.
问题 3. ABCD 是一个平行四边形,P 是它的对角线的交点。如果 O 是参考原点,证明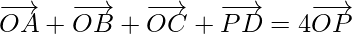

解决方案:
Given that ABCD is a parallelogram, P is the point of intersection of diagonals and O be the point of reference.
So, by using triangle law in △AOP, we get
![]() -(1)
-(1)
By using triangle law in △OBP, we get
![]() -(2)
-(2)
By using triangle law in △OPC, we get
![]() -(3)
-(3)
By using triangle law in △OPD, we get
![]() -(4)
-(4)
Now, on adding equation (1), (2), (3) and (4), we get
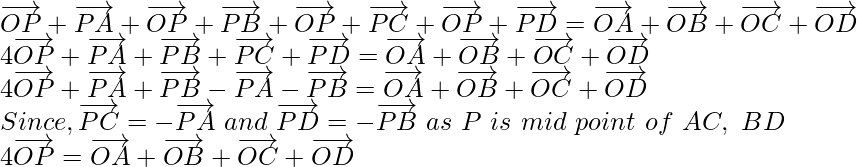
问题 4. 证明连接四边形对边中点的线段相互平分。
解决方案:
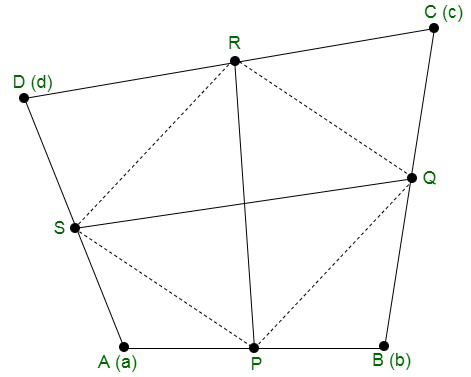
Let us considered ABCD be a quadrilateral and P, Q, R, S be the mid points of sides AB, BC, CD and DA.
So, the position vector of A, B, C and D be
Using the mid point formula
Position vector of P = ![]()
Position vector of Q = ![]()
Position vector of R = ![]()
Position vector of S = ![]()
Position vector of = Position vector of Q – Position vector of P
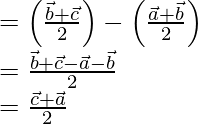 -(1)
-(1)
Position vector of ![]() = Position vector of R – Position vector of S
= Position vector of R – Position vector of S
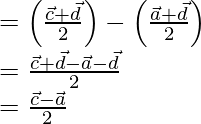 -(2)
-(2)
From eq(1) and (2),
![]()
So, PQRS is a parallelogram and PR bisects QS -(as diagonals of parallelogram)
Hence, proved that the line segments joining the mid-points of
opposite sides of a quadrilateral bisect each other.
问题 5. ABCD 是平面上的四个点,Q 是 AB 和 CD 中点连线的交点;公元前和公元。显示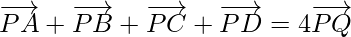 其中 P 是任意点。
其中 P 是任意点。
解决方案:
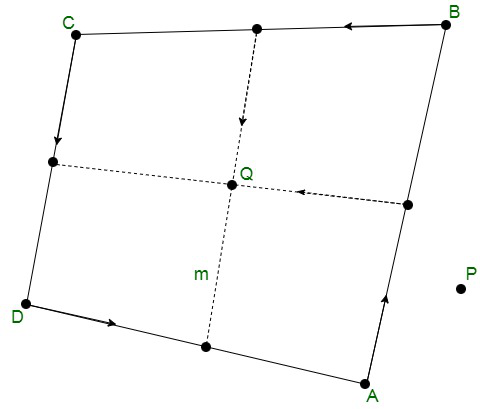
Let us considered the position vector of the points A, B, C and D are![]()
Using the mid-point formula, we get
Position vector of AB = ![]()
Position vector of BC = ![]()
Position vector of CD = ![]()
Position vector of DA = ![]()
It is given that Q is the mid point of the line joining the mid points of AB and CD, so
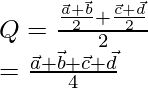
Now, let us assume ![]() be the position vector of P.
be the position vector of P.
So,
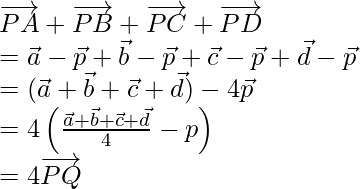
Hence proved
问题 6. 用向量法证明三角形内角的内平分线是同时的。
解决方案:
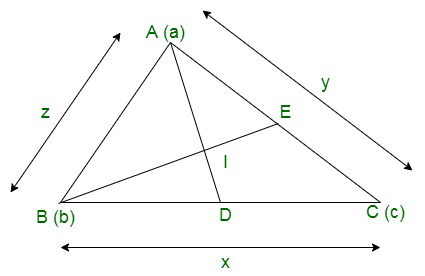
In triangle ABC, let us assume that the position vectors of the vertices of the triangle are ![]()
Length of the sides:
BC = x
AC = y
AB = z
In triangle ABC, the internal bisector divides the opposite side in the ratio of the sides containing the angles.
Since AD is the internal bisector of the ∠ABC, so
BD/DC = AB/AC = z/y -(1)
Therefore, position vector of D = ![]()
Let the internal bisector intersect at point I.
ID/AI = BD/AB -(2)
BD/DC = z/y
Therefore,
CD/BD = z/y
(CD + BD)/BD = (y + z)/z
BC/BD = (y + z)/z
BD = ln/y + z -(3)
So, from eq(2) and (3), we get
ID/AI = ln/(y +z)
Therefore,
Position vector of I =
Similarly, we can also prove that I lie on the internal bisectors of ∠B and ∠C.
Hence, the bisectors are concurrent.