问题1.证明给定位置矢量的点是共线的:
(一世) 
解决方案:
Let x = ![]()
y = ![]()
z = ![]()
Then
![]() = Position vector of (y) – Position vector of (x)
= Position vector of (y) – Position vector of (x)
= ![]()
= ![]()
![]() = Position vector of (z) – Position vector of (y)
= Position vector of (z) – Position vector of (y)
= ![]()
= ![]()
As, ![]()
So, ![]() and
and ![]() are parallel vectors but y is a common point to them. Hence, the given points x, y, z are collinear.
are parallel vectors but y is a common point to them. Hence, the given points x, y, z are collinear.
(ii) 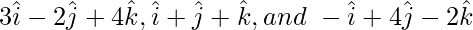
解决方案:
Let
x = ![]()
y = ![]()
z = ![]()
Then,
![]() = Position vector of (y) – Position vector of (x)
= Position vector of (y) – Position vector of (x)
= ![]()
= ![]()
![]() = Position vector of (z) – Position vector of (y)
= Position vector of (z) – Position vector of (y)
= ![]()
= ![]()
As, ![]()
So, ![]() and
and ![]() are parallel vectors but y is a common point to them. Hence, the given points x, y, z are collinear.
are parallel vectors but y is a common point to them. Hence, the given points x, y, z are collinear.
问题2(i)。使用矢量方法,证明A(6,-7,-1),B(2,-3,1)和C(4,-5,0)是共线的。
解决方案:
The points given are A(6, -7, -1), B(2, -3, 1), and C(4, -5, 0)
So, ![]()
![]()
![]()
![]() = Position vector of (B) – Position vector of (A)
= Position vector of (B) – Position vector of (A)
= ![]()
= ![]()
![]() = Position vector of (C) – Position vector of (B)
= Position vector of (C) – Position vector of (B)
=![]()
= ![]()
As, ![]()
So, ![]() and
and ![]() are parallel vectors but B is a common point to them. Hence, the given points A, B, C are collinear.
are parallel vectors but B is a common point to them. Hence, the given points A, B, C are collinear.
问题2(ii)。使用矢量方法,证明A(2,-1,3),B(4,3,1)和C(3,1,2)是共线的。
解决方案:
The points given are A(2, -1, 3), B(4, 3, 1), C(3, 1, 2)
So, the ![]()
![]()
![]()
![]() = Position vector of (B) – Position vector of (A)
= Position vector of (B) – Position vector of (A)
= ![]()
= ![]()
![]() = Position vector of (C) – Position vector of (B)
= Position vector of (C) – Position vector of (B)
= ![]()
= ![]()
As, ![]()
So, ![]() and
and ![]() are parallel vectors but B is a common point to them. Hence, the given points A, B, C are collinear.
are parallel vectors but B is a common point to them. Hence, the given points A, B, C are collinear.
问题2(iii)。使用矢量方法,证明X(1、2、7),Y(2、6、3)和Z(3、10,-1)是共线的。
解决方案:
The points given are X(1, 2, 7), Y(2, 6, 3), Z(3, 10, -1).
So, the ![]()
![]()
![]()
![]() = Position vector of (Y) – Position vector of (X)
= Position vector of (Y) – Position vector of (X)
= ![]()
= ![]()
![]() = = Position vector of (Z) – Position vector of (Y)
= = Position vector of (Z) – Position vector of (Y)
= ![]()
= ![]()
As, ![]()
So, ![]() and
and ![]() are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
问题2(iv)。使用矢量方法,证明X(-3,-2,-5),Y(1、2、3)和Z(3、4、7)是共线的。
解决方案:
The given points are X(-3, -2, -5), Y(1, 2, 3), and Z(3, 4, 7)
So, ![]()
![]()
![]()
![]() = Position vector of (Y) – Position vector of (X)
= Position vector of (Y) – Position vector of (X)
= ![]()
= ![]()
![]() = = Position vector of (Z) – Position vector of (Y)
= = Position vector of (Z) – Position vector of (Y)
= ![]()
= ![]()
As, ![]()
So, ![]() and
and ![]() are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
问题2(v)。使用矢量方法,证明X(2,-1,3),Y(3,-5,1)和Z(-1、11、9)是共线的。
解决方案:
![]()
![]()
![]()
![]() = Position vector of (Y) – Position vector of (X)
= Position vector of (Y) – Position vector of (X)
= ![]()
= ![]()
![]() = = Position vector of (Z) – Position vector of (Y)
= = Position vector of (Z) – Position vector of (Y)
= ![]()
= ![]()
As, ![]()
So, ![]() and
and ![]() are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
问题3(i)。如果 是非零,非共平面向量,证明向量
是非零,非共平面向量,证明向量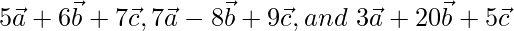 是共面的。
是共面的。
解决方案:
The given vectors are
X = ![]()
Y = ![]()
Z = ![]()
Three vectors are coplanar, if they satisfy the given conditions(for real u and v)
X = u * Y + v * Z
![]()
![]()
On comparing coefficients, we get the following equations
7u + 3v = 5 -(1)
20v – 8u = 6 -(2)
9u + 5v = 7 -(3)
From first two equations, we find that
u = 1/2
v = 1/2
Now put the value of u and v in eq(3)
9(1/2) + 5(1/2) = 7
14/2 = 7
7 = 7
So, the value satisfies the third equation.
Hence, the given vectors X, Y, Z are coplanar.
问题3(ii)。如果 是非零,非共平面向量,证明向量
是非零,非共平面向量,证明向量 是共面的。
是共面的。
解决方案:
The given vectors are
X = ![]()
Y = ![]()
Z = ![]()
Three vectors are coplanar, if they satisfy the given conditions(for real u and v)
X = u * Y + v * Z
![]()
![]()
On comparing coefficients, we get the following equations
-2v = 1 -(1)
3v – 3u = -2 -(2)
5u – 4v = 3 -(3)
From the first two equations, we find that
v = -1/2
u = 1/6
Now put the value of u and v in eq(3)
5(1/6) – 4(-1/2) = 3
5/6 + 2 = 3
(5 + 12)/6 = 3
17/6 ≠ 3
The value doesn’t satisfy the third equation. Hence, the given vectors X, Y, Z are not coplanar.
问题4:证明四个点具有位置向量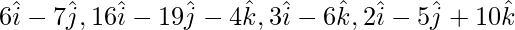 是共面的。
是共面的。
解决方案:
Let the given vectors be
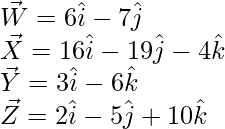
![]() = Position vector of (X) – Position vector of (W)
= Position vector of (X) – Position vector of (W)
= ![]()
= ![]()
![]() = Position vector of (Y) – Position vector of (W)
= Position vector of (Y) – Position vector of (W)
=![]()
= ![]()
![]() = Position vector of (Z) – Position vector of (W)
= Position vector of (Z) – Position vector of (W)
= ![]()
= ![]()
The given vectors are coplanar if,
WX = u(WY) + v(WZ)
![]()
![]()
On comparing coefficients, we get the following equations
-6u – 4v = 10 -(1)
10u + 2v = -12 -(2)
-6u + 10v = -4 -(3)
From the first two equations, we find that
u = -1
v = -1
Now put the value of u and v in eq(3)
-6(-1) + 10(-1) = -4
6 – 10 = -4
-4 = -4
The value satisfies the third equation. Hence, the given vectors W, X, Y, Z are coplanar.
问题5(i)。证明以下向量是共面的显示点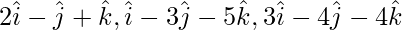
解决方案:
The given vectors are 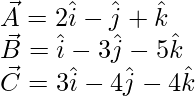
The given vectors are coplanar if,
A = u(B) + v(C)
![]()
![]()
On comparing coefficients, we get the following equations
u + 3v = 2 -(1)
-3u – 4v = -1 -(2)
-5u – 4v = 1 -(3)
From the first two equations, we find that
u = -1
v = 1
Now put the value of u and v in eq(3)
-5(-1) – 4(1) = 1
5 – 4 = 1
1 = 1
The value satisfies the third equation. Hence, the given vectors A, B, C are coplanar.
问题5(ii)。证明以下向量是共面的显示点
解决方案:
The given vectors are 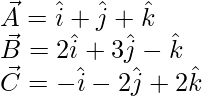
The given vectors are coplanar if,
A = u(B) + v(C)
![]()
![]()
On comparing coefficients, we get the following equations
2u – v = 1 -(1)
3u – 2v = 1 -(2)
-u + 2v = 1 -(3)
From the first two equations, we find that
u = 1
v = 1
Now put the value of u and v in eq(3)
-(1) + 2(1) = 1
1 = 1
The value satisfies the third equation. Hence, the given vectors A, B, C are coplanar.
问题6(i)。证明向量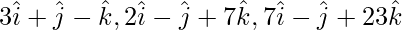 是非共面的。
是非共面的。
解决方案:
The given vectors are 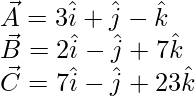
The given vectors are coplanar if,
A = u(B) + v(C)
![]()
![]()
On comparing coefficients, we get the following equations
2u + 7v = 3 -(1)
-u – v = 1 -(2)
7u + 23v = -1 -(3)
From the first two equations, we find that
u = -2
v = 1
Now put the value of u and v in eq(3)
7(-2) + 23(1) = -1
-14 + 23 = -1
-9 ≠ -1
The value does not satisfy the third equation. Hence, the given vectors A, B, C are not coplanar.
问题6(ii)。证明向量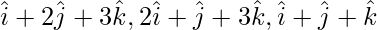 是非共面的。
是非共面的。
解决方案:
The given vectors are 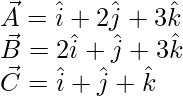
The given vectors are coplanar if,
A = u(B) + v(C)
![]()
![]()
On comparing coefficients, we get the following equations
2u + v = 1 -(1)
u + v = 2 -(2)
3u + v = 3 -(3)
From the first two equations, we find that
u = 0
v = 1
Now put the value of u and v in eq(3)
3(0) + 1 = 3
1 = 3
The value does not satisfy the third equation. Hence, the given vectors A, B, C are not coplanar.
问题7(i)。如果 是非共面的向量,证明给定的向量是非共面的
是非共面的向量,证明给定的向量是非共面的
解决方案:
The given vectors are ![]() )
)
The given vectors are coplanar if,
D = u(E) + v(F)
![]()
![]()
On comparing coefficients, we get the following equations
u + v = 2 -(1)
u + v = -1 -(2)
-2u – 3v = 3 -(3)
There is no value that satisfies the third equation. Hence, the given vectors D, E, F are not coplanar.
问题7(ii)。如果 是非共面的向量,证明给定的向量是非共面的
是非共面的向量,证明给定的向量是非共面的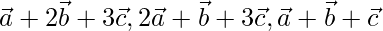
解决方案:
The given vectors are ![]()
The given vectors are coplanar if,
D = u(E) + v(F)
![]()
![]()
On comparing coefficients, we get the following equations
2u + v = 1 -(1)
u + v = 2 -(2)
3u + v = 3 -(3)
From the first two equations, we find that
u = -1
v = 3
Now put the value of u and v in eq(3)
3(-1) + (3) = 3
0 = 3
There is no value that satisfies the third equation. Hence, the given vectors D, E, F are not coplanar.
问题8:证明向量 由
由 是非共面的。表达向量\ vec {d} =
是非共面的。表达向量\ vec {d} = 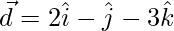 作为向量的线性组合
作为向量的线性组合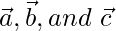 。
。
解决方案:
The given vectors are
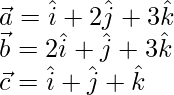
The given vectors are coplanar if,
D = u(E) + v(F)
On comparing coefficients, we get the following equations
2u + v = 1 -(1)
u + v = 2 -(2)
3u + v = 3 -(3)
From above two equations,
u = -1
v = 3
Now put the value of u and v in eq(3)
3(-1) + (3) = 3
0 = -3
There is no value that satisfies the third equation. Hence, the given vectors D, E, F are not coplanar
The given vectors are

The given vectors are coplanar if,
![]()
![]()
![]()
On comparing coefficients, we get the following equations,
x + 2y + z = 2 -(1)
2x + y + z = -1 -(2)
3x + 3y + z = -3 -(3)
From above three equations,
x = -8/3
y = 1/3
z = 4
Therefore, ![]()
问题9.证明三个向量的充要条件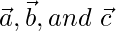 共面的是,它们存在标量l,m,n,并非同时为零,因此
共面的是,它们存在标量l,m,n,并非同时为零,因此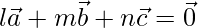
解决方案:
Given conditions: Let us considered ![]() be three coplanar vectors.
be three coplanar vectors.
Then one of them is expressible as a linear combination of other two vectors.
Let,
![]()
![]()
Here, l = x, y = m, n = -1
From above,
![]()
![]()
![]()
Hence, ![]() is a linear combination of two vectors
is a linear combination of two vectors ![]() .
.
Hence proved that ![]() are coplanar vectors.
are coplanar vectors.
问题10:证明带有位置矢量的四个点A,B,C和D 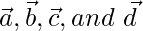 当且仅当
当且仅当 。
。
解决方案:
Given: A, B, C, D be four vectors with position vector ![]()
Let us considered A, B, C, D be coplanar.
Then, there exists x, y, z, u not all zero such that,
![]()
Let us considered x = 3, y = -2, z = 1, y = -2
So, ![]()
and x + y + z + u = 3 – 2 + 1 – 2 = 0
So, A, B, C, D are coplanar.
Let us considered ![]()
![]()
Now on dividing both side by sum of coefficient 4
![]()
![]()
It shows that point P divides AC in the ratio 1:3 and BD in the ratio 2:2 internally,
hence P is the point of intersection of AC and BD.
So, A, B, C, D are coplanar.