第12类RD Sharma解决方案-第28章空间中的直线–练习28.4

问题1.找到点(3，-1，11)与直线的垂直距离 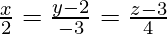$\frac{x}{2}=\frac{y-2}{-3}=\frac{z-3}{4}$

解决方案：

Let the foot of the perpendicular drawn from P (3, -1, 11) to the line  $\frac{x}{2}=\frac{y-2}{-3}=\frac{z-3}{4}$is Q, so we have to find length of PQ is general point on the line $\frac{x}{2}=\frac{y-2}{-3}=\frac{z-3}{4}=\lambda (say)$

Coordinate of Q = $(2\lambda,-3\lambda+2,4\lambda+3)$, direction ratios of the given line = 2,-3,4. Since PQ is the perpendicular to the given line interface. 

$a_1a_2+b_1b_2+c_1c_2=0$

$\Rightarrow 2(2\lambda-3)+(-3 )(-3\lambda+3)4(4\lambda-8)=0$

$\Rightarrow 4\lambda-6+9\lambda-9+16\lambda-32=0$

$29\lambda-47=0; \lambda = \frac{47}{29}$

So, the coordinates of Q are:

$\Rightarrow 2(\frac{47}{29}),-3(\frac{47}{29})+2,4(\frac{47}{29})+3 = \frac{94}{29},\frac{-83}{29},\frac{275}{29}$

Distance between P and Q is given as:

$= \sqrt{(\frac{94}{29}-3)^2+(\frac{-83}{29}+1)^2+(\frac{275}{29}-11)^2}$

$= \sqrt{(\frac{7}{29})^2+(\frac{-54}{29})^2+(\frac{-44}{29})^2}$

$=\sqrt{\frac{49}{841}+\frac{2916}{841}+\frac{1936}{841}}$

$=\sqrt{\frac{4901}{841}}$

So, the required distance is $\sqrt{\frac{4901}{841}}$units

问题2.找到点(1,0,0)与直线的垂直距离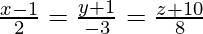$\frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+10}{8}$ 。此外，找到垂直脚的坐标和垂直方程。

解决方案：

Let us consider the foot of the perpendicular drawn from P (1,0,0) to the line $\frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+10}{8}$is Q. So let us find the length of PQ i.e. $\frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+10}{8}=\lambda$

Coordinate of Q = $(2\lambda+1, -3\lambda-1, 8\lambda-10)$

The direction ratios of the given line:  $a_1a_2+b_1b_2+c_1c_2=0$

$\Rightarrow 2(2\lambda)+(-3)(-3\lambda-1)+8(8\lambda-10)=0$

$4\lambda+9\lambda+3+64\lambda-80=0$

$\Rightarrow 77\lambda-77=0; \lambda = 1$

So the Coordinates of Q are as follows:

$(2\lambda+1, -3\lambda-1, 8\lambda-10)= [2(1)+1,-3(1)-1,8(1)-10]= [3,4,-2]$

Distance between P and Q is given by:

PQ = $\sqrt{(x1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

PQ = $\sqrt{(1-3)^2+(0+4)^2+(0+2)^2}=\sqrt{4+16+4}$

PQ = $\sqrt{24} = 2\sqrt{6}$

Hence, the foot of the perpendicular = (3,-4,-2);

Length of the perpendicular = $2\sqrt{6}$units.

问题3.找到从点A(1,0,3)到点B(4,7,1)和点C(3,5,3)的交点的垂线的底脚。

解决方案：

Let us consider, the foot of the perpendicular drawn from A(1,0,3) to the line joining

Points B(4,7,1) and C(3,5,3) be D. The equation of the line passing through 

points B(4,7,1) and C(3,5,3) is 

$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

$\Rightarrow \frac{x-4}{3-4}=\frac{y-7}{5-7}=\frac{z-1}{3-1}$

$\Rightarrow \frac{x-4}{-1}=\frac{y-7}{-2}=\frac{z-1}{2}$

Let $\frac{x-4}{-1}=\frac{y-7}{-2}=\frac{z-1}{2}=\lambda$

So, the direction ratio of AD is $(-\lambda+4-1),(-2\lambda+7-0),(2\lambda+1-3) = (-\lambda+3),(-2\lambda+7),(2\lambda-2)$

Line AD is the perepndicular to BC so, $a_1a_2+b_1b_2+c_1c_2=0$

$\Rightarrow -1(-\lambda+3)+(2)(-2\lambda+7)+2(2\lambda-2)=0$

$\Rightarrow 9\lambda -21 = 0; \lambda = \frac{21}{9}$

Hence, coordinates of D are: $\left(\frac{-21}{9}+4,(-2)(\frac{21}{9}+7),2(\frac{21}{9}+1)\right)$

= $\left(\frac{15}{9},\frac{21}{9},\frac{51}{9}\right) = \left(\frac{5}{3},\frac{7}{3},\frac{17}{3}\right)$

问题4：A(1,0,4)，B(0，-11,3)，C(2，-3,1)是三个点，D是与BC上A相垂直的脚。找出D的座标。

解决方案：

Given: D is the perpendicular from A(1,0,4) on BC. So,

Equation of line passing through BC is:

$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

$\frac{x-0}{2-0}=\frac{y+11}{-3+11}=\frac{z-3}{1-3}$

$\frac{x}{2}=\frac{y+11}{8}=\frac{z-3}{-2}$

$\frac{x}{2}=\frac{y+11}{8}=\frac{z-3}{-2}=\lambda$

Coordinates of D = ( $2\lambda, 8\lambda-11,-2\lambda+3$)

Direction ratios of AD is $(2\lambda-1),(8\lambda-11-0),(-2\lambda+3-4)= (2\lambda-1),(8\lambda-11),(-2\lambda-1)$

Line AD is perpendicular to BS so, 

$a_1a_2+b_1b_2+c_1c_2=0$

$2(2\lambda-1)+8(8\lambda-11)+(-2)(-2\lambda-1)=0$

$72\lambda-88 = 0; \lambda = \frac{88}{72} or \frac{11}{9}$

So, coordinates of D are = $(2\lambda,8\lambda-11,-2\lambda+3)$

$\left(2(\frac{11}{9}),8(\frac{11}{9})-11,-2(\frac{11}{9})+3\right)$=

$\left(\frac{22}{9},\frac{-11}{9},\frac{5}{9}\right)$

问题5.找到从点(2,3,4)到直线的垂直线的底脚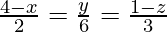$\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$ 。同样，找到从给定点到直线的垂直距离。

解决方案：

Let us consider that The foot of the perpendicular drawn from P(2,3,4) to the line

$\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$is $\theta$.

Equation of the line is $\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$

Let $\frac{x-4}{-2}=\frac{y}{6}=\frac{z-1}{-3} = \lambda$

Coordinates of Q = $(-2\lambda+4-2),(6\lambda-3),(-3\lambda+1-4) = (-2\lambda+2),(6\lambda-3),(-3\lambda-3)$

So, PQ is perpendicular to the given line,  $a_1a_2+b_1b_2+c_1c_2=0$

$(-2)(-2\lambda+2)+6(6\lambda-3)+(-3)(-3\lambda-3)=0$

$49\lambda-13=0; \lambda=\frac{13}{49}$

Coordinates of Q = $(-2\lambda+4, 6\lambda. -3\lambda+1)$

= $\left(-2(\frac{13}{49})+4,6(\frac{13}{49}),-3(\frac{13}{49})+1\right)$

= $\left(\frac{-26+196}{49},\frac{78}{49},\frac{-39+49}{49}\right)= \left(\frac{170}{49}, \frac{78}{49},\frac{10}{49}\right)$

Distance between P and Q is given by: PQ = $\sqrt{(x1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

= $\sqrt{(\frac{170}{49}-2)^2+(\frac{78}{49}-3)^2+(\frac{10}{49}-4)^2}$

= $\sqrt{\frac{44541}{2401}} = \sqrt{\frac{909}{49}} = \frac{3\sqrt{101}}{49}$

Hence, perpendicular distance from (2,3,4) to the given line is $\frac{3\sqrt{101}}{49}$units.

问题6.找到从点P(2,4，-1)到直线的垂线方程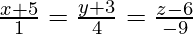$\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}$ 。另外，从P记下垂直脚的坐标。

解决方案：

Let $\theta$ be the foot of thr perpendicular drawn from P(2,4,-1) to the line

$\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}$

Given line is $\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9} = \lambda (say)$

Coordinate of Q (General point on the line) = $(\lambda-5, 4\lambda-3, -9\lambda+6)$

Direction ratios of PQ are: $(\lambda-5-2),(4\lambda-3-4),(-9\lambda+6+1) = \lambda-7, 4\lambda-7, -9\lambda+7$

As line PQ is perpendicular to the given line, so: $a_1a_2+b_1b_2+c_1c_2=0$

$1(\lambda-7)+4(4\lambda-7)+(-9)(-9\lambda+7)=0$

$98\lambda-98=0; \lambda=1$

Therefore, coordinates of foot of perpendicular = {-4, 1, -3}

So equation of the perpendicular PQ is : $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

$\Rightarrow \frac{x-2}{-4-2}=\frac{y-4}{1-4}=\frac{z+1}{-3+1}$

$\Rightarrow \frac{x-2}{-6}=\frac{y-4}{-3}=\frac{z+1}{-2}$

问题7.找到从点(5,4，-1)到直线的垂线的长度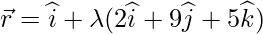$\vec{r}=\widehat{i} + \lambda(2\widehat{i} + 9\widehat{j}+5\widehat{k})$

解决方案：

Let the foot of the perpendicular drawn from P(5,4,-1) to the given line is Q, so given equation of line is:

$\vec{r}=\widehat{i} + \lambda(2\widehat{i} + 9\widehat{j}+5\widehat{k})$

$(x\widehat{i}+y\widehat{j}+z\widehat{k}) = (1+2\lambda)\widehat{i}+(9\lambda)\widehat{j}+(5\lambda)\widehat{k}$

Equating the coefficients of $\widehat{i}, \widehat{j}, \widehat{k}$

$\Rightarrow x = 1+2\lambda, y = 9\lambda, z = 5\lambda$

$\Rightarrow \frac{x-1}{2} = \lambda, \frac{y}{9} = \lambda, \frac{z}{5}=\lambda$

$\Rightarrow \frac{x-1}{2} = \frac{y}{9} =\frac{z}{5}=\lambda (say)$

Coordinate of Q = $(2\lambda+1,9\lambda,5\lambda)$

Direction ratios of line PQ are: $(2\lambda+1-5),9\lambda-4,5\lambda+1$

$\Rightarrow 2\lambda-4, 9\lambda-4, 5\lambda+1$

As line PQ is perpendicular to the given line, so: $a_1a_2+b_1b_2+c_1c_2=0$

$2(2\lambda-4)+9(9\lambda-4)+5(5\lambda+1)=0$

$\Rightarrow 4\lambda - 8 +81\lambda - 36 +25\lambda + 5 = 0$

$\Rightarrow 110\lambda - 39 = 0; \lambda = \frac{39}{110}$

Coordinate of Q = { $2\lambda+1, 9\lambda, 5\lambda$ }

= $\left(2(\frac{39}{110})+1,9(\frac{39}{110}),5(\frac{39}{110})\right)$

= $\left(\frac{188}{110},\frac{351}{110},\frac{195}{110}\right)$

Length of perpendicular = PQ = $\sqrt{(x1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

= $\sqrt{(5-\frac{188}{110})^2+ (4-\frac{351}{110})^2+(-1-\frac{195}{110})^2}$

  PQ = $\sqrt{\frac{231990}{12100}} or \sqrt{\frac{2109}{110}}$ 

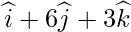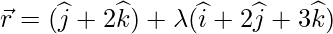问题8.找到从该点绘制的垂直线的脚$\widehat{i}+6\widehat{j}+3\widehat{k}$到线$\vec{r} = (\widehat{j}+2\widehat{k}) + \lambda(\widehat{i}+2\widehat{j}+3\widehat{k})$ 。另外，找到垂直线的长度。

解决方案：

Let position vector of foot of perpendicular drawn from p $(\widehat{i}+6\widehat{j}+3\widehat{k})$on $\vec{r} = (\widehat{j}+2\widehat{k}) + \lambda(\widehat{i}+2\widehat{j}+3\widehat{k})$ be Q $(\vec{q})$. So, Q is on the line $\vec{r} = (\widehat{j}+2\widehat{k}) + \lambda(\widehat{i}+2\widehat{j}+3\widehat{k})$

So, position vector of Q = $\lambda(\widehat{i})+(1+2\lambda)\widehat{j}+(2+3\lambda)\widehat{k}$

$\vec{PQ}$is the position vector of Q – position vecor of p = $(\lambda\widehat{i}+(1+2\lambda)\widehat{j}-(\widehat{i}+6\widehat{j}+3\widehat{k})$

$\vec{PQ} = (\lambda-1)\widehat{i}+(2\lambda-5)\widehat{j}+(3\lambda-1)\widehat{k}$

Here, PQ vector is perpendicular to the given line. So,

$(\lambda-1)\widehat{i}+(2\lambda-5)\widehat{j}+(3\lambda-1)\widehat{k} = 0$ 

$\Rightarrow (\lambda-1)1+(2\lambda-5)2+(3\lambda-1)3 = 0$

$14\lambda -14 = 0; \lambda = 1$

Position vector of Q = {$(\widehat{j}+2\widehat{j})+\lambda(\widehat{i}+2\widehat{j}+3\widehat{k})$}

= $(\widehat{j}+2\widehat{k})+1(\widehat{i}+2\widehat{j}+3\widehat{k})$

Foot of the perpendicular = $\widehat{i}+3\widehat{j}+5\widehat{k}$

$\vec{PQ}$= Position vector of Q – Position vector of P

= $(\widehat{i}+3\widehat{j}+5\widehat{k})-(\widehat{i}+6\widehat{j}+3\widehat{k})$

= $-3\widehat{i}+2\widehat{k}$

$|\vec{PQ}|$ = $\sqrt{(-3)^2+(2)^2} = \sqrt{13}$ units

问题9.从点P(-1,3,2)到直线找到垂直drwan的方程式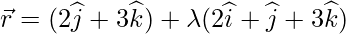$\vec{r} = (2\widehat{j}+3\widehat{k})+\lambda(2\widehat{i}+\widehat{j}+3\widehat{k})$ 。另外，从P查找垂直脚的坐标。

解决方案：

Let Q be the perpendicular drawn from P {$-\widehat{i}+3\widehat{j}+2\widehat{k}$} on the 

vector $\vec{r} = (2\widehat{j}+3\widehat{k})+\lambda(2\widehat{i}+\widehat{j}+3\widehat{k})$

Let the position vector of Q be : $(2\widehat{i}+3\widehat{k})+ \lambda(2\widehat{i}+\widehat{j}+3\widehat{k})$

                                                      : $(2\lambda)\widehat{i}+(2+\lambda)\widehat{j}+(3+3\lambda)\widehat{k}$

$\vec{PQ}$= Position Vector of Q – Position Vector of P = $(2\lambda)\widehat{i}+(2+\lambda)\widehat{j}+(3+3\lambda)\widehat{k} - (-\widehat{i}+3\widehat{j}+2\widehat{k})$

$\vec{PQ} = (2\lambda+1)\widehat{i} + (\lambda-1)\widehat{j}+(3\lambda+1)\widehat{k}$

As PQ vector is perpendicular to the given line, 

$(2\lambda+1)\widehat{i} + (\lambda-1)\widehat{j}+(3\lambda+1)\widehat{k} = 0$

$4\lambda+2+\lambda-1+9\lambda+3 = 0; \lambda= \frac{-4}{14} or \frac{-2}{7}$

Position Vector of Q = $(2\lambda)\widehat{i}+(2+\lambda)\widehat{j}+(3+3\lambda)\widehat{k}$ is

$2(\frac{-2}{7})\widehat{i}+(2-\frac{2}{7})\widehat{j}+(3+3(\frac{-2}{7})\widehat{k})$

$\frac{-4}{7}\widehat{i}+\frac{12}{7}\widehat{j}+\frac{15}{7}\widehat{k}$

Coordinates of foot of the perpendicular: $\left(\frac{-4}{7},\frac{12}{7},\frac{15}{7}\right)$

Equation of PQ is: $\vec{r} = \vec{a}+\lambda(\vec{b}-\vec{a})$

$\Rightarrow \vec{r} = (-\widehat{i}+3\widehat{j}+2\widehat{k})+\lambda((\frac{-4}{7}\widehat{i}+\frac{12}{7}\widehat{j}+\frac{15}{7}\widehat{k})-(-\widehat{i}+3\widehat{j}+2\widehat{k}))$

$\vec{r} = (-\widehat{i}+3\widehat{j}+2\widehat{k}) + \lambda(\frac{3}{7}\widehat{i}-\frac{9}{7}\widehat{j}+\frac{1}{7}\widehat{k})$

$\vec{r} = (-\widehat{i}+3\widehat{j}+2\widehat{k}) + \mu(3\widehat{i}-9\widehat{j}+\widehat{k})$

问题10.从直线上的(0,2,7)找到垂直线的底脚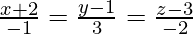$\frac{x+2}{-1}=\frac{y-1}{3}=\frac{z-3}{-2}$

解决方案：

Let the foot of the perpendicular drawn from (0,2,7) to the line  $\frac{x+2}{-1}=\frac{y-1}{3}=\frac{z-3}{-2}$ be Q. 

Given equation of the line is $\frac{x+2}{-1}=\frac{y-1}{3}=\frac{z-3}{-2} = \lambda (say)$

Coordinate of Q = {$-\lambda-2, 3\lambda+1, -2\lambda+3$} 

Direction Ratios of PQ are  $(\lambda-2-0), (3\lambda+1-2), (-2\lambda+3-7) = (-\lambda-2),(3\lambda-1),(-2\lambda- 4)$

Since, PQ is perpendicular to the given line, so $a_1a_2+b_1b_2+c_1c_2=0$

$-1(-\lambda-2)+3(3\lambda-1)+(-2)(-2\lambda-4)=0$

$\Rightarrow \lambda+2+9\lambda-3+4\lambda+8=0$

$\Rightarrow 14\lambda + 7 =0; \lambda = \frac{-1}{2}$

Foot of the perpendicular = {$\lambda-2, 3\lambda+1, -2\lambda+3$}\

= $\left(-(\frac{-1}{2})-2, 3(\frac{-1}{2}),-2(\frac{-1}{2})+3\right)$

$\left(\frac{-3}{2}, \frac{-1}{2}, 4\right)$

问题11.找到(1,2，-3)到直线的垂直线的底脚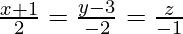$\frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1}$

解决方案：

Let the foot of perpendicular from P (1,2,-3) to the line  $\frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1}$ be Q.

Given the equation of line is $\frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1} =\lambda (say)$

$\Rightarrow x = 2\lambda-1, y=-2\lambda+3, z = -\lambda$

Coordinates of Q are {$2\lambda-1, -2\lambda+3, -\lambda$}

Direction Ratios of PQ are:  $(2\lambda-1-1), (-2\lambda+3-2), (-\lambda+3)$ =

$(2\lambda-2), (-2\lambda+1), (-\lambda+3)$

Let PQ be the perpendicular to th egiven line, so $a_1a_2+b_1b_2+c_1c_2=0$

$2(2\lambda-2)+(-2)(-2\lambda+1)+(-1)(-\lambda+3)=0$

$9\lambda-9 = 0; \lambda = 1$

Coordinate of the perpendicular: $(2\lambda-1, -2\lambda+3, -\lambda)$

$\Rightarrow (2(1)-1, -2(1)+3, -1) = (1,1,-1)$

问题12。找到通过点A(0,6，-9)和B(-3，6，3)的直线方程。如果D是从直线AB上的点C(7,4，-1)绘制的垂直线的脚，则找到点D的坐标和直线CD的方程式。

解决方案：

Equation of line AB is  $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

$\Rightarrow \frac{x-0}{3-0}=\frac{y-6}{-6-6}=\frac{z+9}{3+9}$

$\Rightarrow \frac{x-0}{3-0}=\frac{y-6}{-6-6}=\frac{z+9}{3+9} = \lambda (say)$

Coordinate of point D = {$-3\lambda, -12\lambda+6, 12\lambda-9$}

Direction ratios of CD = $(-3\lambda-7)+(-12)(-12\lambda+6-4)+12(12\lambda-9+1)$

= $(-3\lambda-7)+(-12)(-12\lambda+2)+12(12\lambda-8)$

As line CD is perpendicular to the line AB, so  $a_1a_2+b_1b_2+c_1c_2=0$

$-3(-3\lambda-7)+(-12)(-12\lambda+2)+12(12\lambda-8) =0$

$297\lambda-99=0; \lambda = \frac{1}{3}$

Coordinate of D = {$-3\lambda, -12\lambda+6, 12\lambda-9$}

= {$-3(\frac{1}{3}), -12(\frac{1}{3})+6, 12(\frac{1}{3})-9$}

= (-1,2,-5)

Equation of CD is $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$ 

$\Rightarrow \frac{x-7}{-1-7}=\frac{y-4}{2-4}=\frac{z+1}{-5+1}$

$\Rightarrow \frac{x-7}{-8}=\frac{y-4}{-2}=\frac{z+1}{-4}$

$\Rightarrow \frac{x-7}{4}=\frac{y-4}{1}=\frac{z+1}{2}$

问题13.找到点(2,4，-1)与直线的距离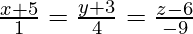$\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}$

解决方案：

Let P = (2,4,-1)

In order to find the distance we need to find a point Q on the line. We see that line is passing through 

the point Q(-5,-3,6). So, let’s take this point as the required point. 

The line is also parallel to the vector $\vec{b} = \widehat{i} +4\widehat{j} -9\widehat{k}$

Now, $\vec{PQ}$ = $(-5\widehat{i}-3\widehat{j}+6\widehat{k})-(2\widehat{i}+4\widehat{j}-\widehat{k})=-7\widehat{i}-7\widehat{j}+7\widehat{k}$

$\vec{b} \times \vec{PQ} = \begin{vmatrix} \widehat{i} & \widehat{j} & \widehat{k} \\ 1 & 4 & -9 \\ -7 & -7 & 7 \end{vmatrix}= -35\widehat{i}+56\widehat{j}+21\widehat{k}$

$|\vec{b} \times \vec{PQ}| = \sqrt{1225+3136+441} = \sqrt{4802}$

$\vec{b} = \sqrt{1+16+81} = \sqrt{98}$

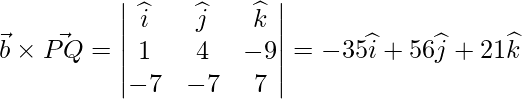
Therefore, 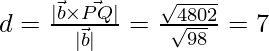$d= \frac{|\vec{b} \times \vec{PQ}|}{|\vec{b}|} = \frac{\sqrt{4802}}{\sqrt{98}}=7$

问题14.找到从点A(1,8,4)到连接点B(0，-1,3)和C(2，-3，-1)的线的垂直线的脚坐标。

解决方案：

Let L be the foot of the perpendicular drawn from A(1,8,4) on the line joining the points B(0,-1,3) and C(2,-3,-1). 

Equation of the line passing through the points B and C is given by 

$\vec{r}=\vec{b}+\lambda(\vec{c}-\vec{b})$

$\vec{r} = (0+2\lambda)\widehat{i}+(-1-2\lambda)\widehat{j}+(3-4\lambda)\widehat{k}$

Let position vector of L be, 

$\vec{r}=(2\lambda)\widehat{i}+(-1-2\lambda)\widehat{k}+(3-4\lambda)\widehat{k}......(Equation 1)$

Then, $\vec{AL}$ = Position vector of L – Position vector of A

$\Rightarrow \vec{AL} = (2\lambda)\widehat{i}+(-1-2\lambda)\widehat{j}+(3-4\lambda)\widehat{k}-(1\widehat{i}+8\widehat{j}+4\widehat{k})$

Since, AL vector is perpendicular to the given line

which is parallel to $\vec{b}=2\widehat{i}-2\widehat{j}-4\widehat{k}$

Therefore, $\vec{AL}\cdot\vec{b}=0$

$\Rightarrow 2(-1+2\lambda)-2(-9-2\lambda)-4(-1-4\lambda)=0$

$24\lambda+20=0; \lambda=\frac{-5}{6}$

Putting value of lambda in Equation 1, we get:

$\vec{r} = \frac{-5}{3}\widehat{i}+\frac{2}{3}\widehat{j}+\frac{19}{3}\widehat{k}$

So, coordinates of foot of the perpendicular are

 $\left(\frac{-5}{3}, \frac{2}{3}, \frac{19}{3}\right)$