第 12 课 RD Sharma 解决方案 – 第 28 章空间直线 – 练习 28.2 |设置 2
问题 13. 求通过点 (-1, 2, 1) 并平行于直线的直线方程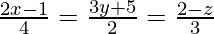 .
.
解决方案:
The equation of line ![]() can be re-written as,
can be re-written as,
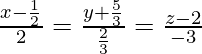
The direction ratios of the line parallel to line ![]() are proportional to 2, 2/3, -3.
are proportional to 2, 2/3, -3.
Equation of the required line passing through the point ( -1, 2, 1) having direction ratios proportional to (2, 2/3, -3) is,
![]()
=> ![]()
问题 14. 求通过点 (2, -1, 3) 并平行于直线的直线方程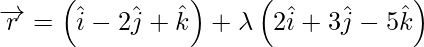 .
.
解决方案:
The given line ![]() is parallel to the vector
is parallel to the vector ![]()
And the required line is also parallel to the given line.
So, the required line is parallel to the vector ![]()
Hence, the equation of the required line passing through the point (2,-1, 3) and parallel to the vector ![]() is,
is,
=> ![]()
问题 15. 求通过点 (2, 1, 3) 并垂直于这些线的线的方程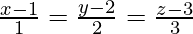 和
和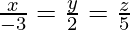 .
.
解决方案:
Let,
![]()
![]()
Since the required line is perpendicular to the lines parallel to the vectors ![]() and
and ![]() , it is also parallel to the vector
, it is also parallel to the vector ![]()
Now,
![]()
= 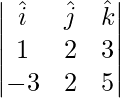
= ![]()
= ![]()
Thus, the direction ratios of the required line are proportional to 2, -7, 4.
The equation of the required line passing through the point (2, 1, 3) and having direction ratios proportional to 2, -7, 4 is
=> ![]()
问题 16. 求通过该点的线的方程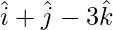 并且垂直于线条
并且垂直于线条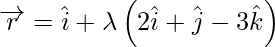 和
和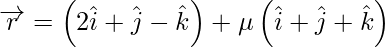 .
.
解决方案:
The required line is perpendicular to the lines parallel to the vectors ![]() and
and ![]() .
.
So, the required line is parallel to the vector,
![]()
= 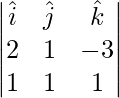
= ![]()
Equation of the required line passing through the point ![]() and parallel to
and parallel to ![]() is,
is,
=> ![]()
问题 17. 求通过点 (1, -1, 1) 并垂直于连接点 (4, 3, 2)、(1, -1, 0)和 (1, 2, -1), (2, 1, 1)。
解决方案:
The direction ratios of the line joining the points (4, 3, 2), (1, -1, 0) and (1, 2, -1), (2, 1, 1) are -3, -4, -2 and 1, -1, 2 respectively.
Let,
![]()
![]()
Since the required line is perpendicular to the lines parallel to the vectors ![]() and
and ![]() , it is parallel to the vector
, it is parallel to the vector ![]()
Now,
![]()
= 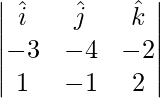
= ![]()
So, the direction ratios of the required line are proportional to -10, 4, 7.
The equation of the required line passing through the point (1,-1, 1) and having direction ratios proportional to -10, 4, 7 is
=> ![]()
问题 18. 确定通过点 (1, 2, -4) 并垂直于两条线的线的方程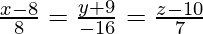 和
和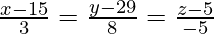 .
.
解决方案:
We have,
![]()
![]()
Let,
![]()
![]()
Since the required line is perpendicular to the lines parallel to the vectors ![]() and
and ![]() , it is parallel to the vector
, it is parallel to the vector ![]()
Now,
![]()
= 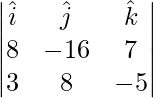
= ![]()
The direction ratios of the required line are proportional to 24, 61, 112.
The equation of the required line passing through the point (1, 2,-4) and having direction ratios proportional to 24, 61, 112 is,
=> ![]()
问题 19. 证明这些线条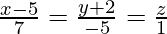 和
和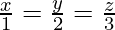 是相互垂直的。
是相互垂直的。
解决方案:
The direction ratios of the line ![]() are proportional to 7, -5, 1 respectively.
are proportional to 7, -5, 1 respectively.
And the direction ratios of the line ![]() are proportional to 1, 2, 3 respectively.
are proportional to 1, 2, 3 respectively.
Let,
![]()
![]()
Now,
![]()
= 7 – 10 + 3
= 0
So, ![]()
Therefore, the given lines are perpendicular to each other.
Hence proved.
问题 20. 求通过平行于线 6x - 2 = 3y + 1 = 2z - 2 的点 (2, -1, -1) 的线的向量方程。
解决方案:
The equation of the line 6x − 2 = 3y + 1 = 2z − 2 can be re-written as
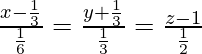
=> ![]()
Since the required line is parallel to the given line, the direction ratios of the required line are proportional to 1,2,3.
The vector equation of the required line passing through the point (2,-1,-1) and having direction ratios proportional to 1,2,3 is,
=> ![]()
问题 21. 如果线条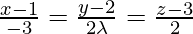 和
和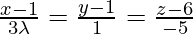 是垂直的,求 λ 的值。
是垂直的,求 λ 的值。
解决方案:
The equations of the given lines are,
![]()
![]()
Since the given lines are perpendicular to each other, we have
=> -3 (3λ) + 2λ (1) + 2 (-5) = 0
=> -9λ + 2λ – 10 = 0
=> -7λ = 10
=> λ = -10/7
Therefore, the value of λ is -10/7.
问题 22. 如果 A、B、C、D 点的坐标为 (1, 2, 3), (4, 5, 7), (-4, 3, -6) 和 (2, 9, 2)分别求直线 AB 和 CD 的夹角。
解决方案:
The direction ratios of AB and CD are proportional to 3, 3, 4 and 6, 6, 8, respectively.
Let θ be the angle between AB and CD. Then,
![]()
= ![]()
= 1
Now cos θ = 1
=> θ = 0°
Therefore, the angle between AB and CD is 0°.
问题 23.求 λ 的值,使以下直线相互垂直。
![]()
解决方案:
The equation of the given line ![]() can be re-written as,
can be re-written as,
![]()
The equation of the given line ![]() can be re-written as,
can be re-written as,
![]()
Since the given lines are perpendicular to each other, we have
=> (5λ + 2) (1) – 5 (2λ) + 1 (3) = 0
=> 5λ + 2 – 10λ + 3 = 0
=> -5λ = -5
=> λ = 1
Therefore, the value of λ is 1.
问题 24. 求直线的方向余弦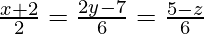 .此外,找到通过点 A(-1, 2, 3) 并平行于给定线的线的矢量方程。
.此外,找到通过点 A(-1, 2, 3) 并平行于给定线的线的矢量方程。
解决方案:
The equation of the given line is,
![]()
The given equation can be re-written as
![]()
This line passes through the point (-2, 7/2, 5) and has direction ratios proportional to 2, 3, −6.
So, its direction cosines are 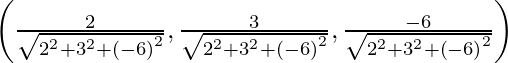
Or, ![]()
The required line passes through the point having position vector ![]() .
.
And also it is parallel to the vector ![]() .
.
So, its vector equation is,
=> ![]()