第 12 课 RD Sharma 解决方案 – 第 28 章空间直线 – 练习 28.3

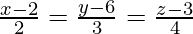问题 1. 显示线条$\frac{x}{1}=\frac{y-2}{2}=\frac{z+3}{3}$和$\frac{x-2}{2}=\frac{y-6}{3}=\frac{z-3}{4}$相交并找到它们的交点。

解决方案：

Given that the coordinates of any point on the first line are 

$\frac{x}{1}=\frac{y-2}{2}=\frac{z+3}{3}=\lambda$

⇒ x = λ, y = 2λ + 2, z = 3λ – 3 

The coordinates of a general point on the second line are given by:

$\frac{-2}{2}=\frac{y-6}{3}=\frac{z-3}{4}=\mu$

⇒ x = 2μ + 2, y = 3μ + 6, z = 4μ + 3

If the lines intersect, for some values of λ and μ, we must have:

λ – 2μ = 2              ……(1)

2λ – 3μ = 4          ……(2)

3λ – 4μ = 6           …..(3)

Solving this system of equations, we get

λ = 2 and μ = 0

On substituting the values in eq(3), we have

LHS = 3(2) – 4(0) 

= 6 = RHS

Thus, the given lines intersect at (2, 6, 3).

问题 2. 显示线条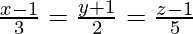$\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-1}{5}$和$\frac{x+2}{4}=\frac{y-1}{3}=\frac{z+1}{-2}$不要相交。

解决方案：

Given that the coordinates of any point on the first line are 

$\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-1}{5}=\lambda$

⇒ x = 3λ + 1, y = 2λ – 1, z = 5λ + 1

The coordinates of a general point on the second line are given by:

$\frac{x+2}{4}=\frac{y-1}{3}=\frac{z+1}{-2}=\mu$

⇒ x = 4μ – 2, y = 3μ + 1, z = -2μ – 1

If the lines intersect, for some values of λ and μ, we must have:

3λ – 4μ = -3             ……(1)

2λ – 3μ = 2              ……(2)

5λ + 2μ = -2            …..(3)

Solving this system of equations, we get

λ = -17 and μ = -12

On substituting the values in eq(3), we have

LHS = 3(-17) + 2(-12)

= -75 ≠ RHS

Thus, the given lines do not intersect with each other.

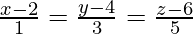问题 3. 显示线条$\frac{x+1}{3}=\frac{y+3}{5}=\frac{z+5}{7}$和$\frac{x-2}{1}=\frac{y-4}{3}=\frac{z-6}{5}$相交并找到它们的交点。

解决方案：

Given that the coordinates of any point on the first line are 

$\frac{x+1}{3}=\frac{y+3}{5}=\frac{z+5}{7}=\lambda$

⇒ x = 3λ – 1, y = 5λ – 3, z = 7λ – 5

The coordinates of a general point on the second line are given by:

$\frac{x-2}{1}=\frac{y-4}{3}=\frac{z-6}{5}=\mu$

⇒ x = 2μ + 2, y = 3μ + 6, z = 4μ + 3

If the lines intersect, for some values of λ and μ, we must have:

3λ – μ = 3               ……(1)

5λ – 3μ = 7            ……(2)

7λ – 5μ = 11           …..(3)

Solving this system of equations, we get

λ = 1/2 and μ = -3/2

On substituting the values in eq(3), we have

LHS = 3(2) – 4(0)

= -3/2 = RHS

Now put the value of λ in first equation and we get

x = 1/2, y = -1/2, z = -3/2

Thus, the given lines intersect at (1/2, -1/2, -3/2).

问题 4. 证明通过 (0, -1, -1) 和 B(4, 5, 1) 的线与通过 C(3, 9, 4) 和 D(-4, 4, 4) 的线相交。另外，找到它们的交点。

解决方案：

Given that the coordinates of any point on the line AB are 

$\frac{x-0}{4-0}=\frac{y+1}{5+1}=\frac{z+1}{1+1}=\lambda$

⇒ x = 4λ, y = 6λ – 1, z = 2λ – 1

Also, given that the coordinates of any point on the line CD are 

$\frac{x-3}{3+4}=\frac{y-9}{9-4}=\frac{z-4}{4-4}=\mu$

⇒ x = 7μ + 3, y = 5μ + 9, z = 4

If the lines intersect, for some values of λ and μ, we must have:

4λ – 7μ = 3            ……(1)

6λ – 5μ = 10         ……(2)

λ = 5/2                  …..(3)

⇒ λ = 5/2 and μ = 1.

On substituting the values in eq(3), we have

LHS = 4(5/2) – 7(1)

= 3 = RHS

Now put the value of λ in line AB, we get

x = 10, y = 14, z = 4

Thus, the given lines AB and CD intersect at point (10, 14, 4).

问题 5. 证明这条线$\vec{r}=(\hat{i}+\hat{j}-\hat{k})+λ(3\hat{i}-\hat{j})$和$\vec{r}=(4\hat{i}-\hat{k})+μ(2\hat{i}+3\hat{k})$相交并找到它们的交点。

解决方案：

According to the question, it is given that the position vector of two points on the lines are

$\vec{r}=(\hat{i}+\hat{j}-\hat{k})+λ(3\hat{i}-\hat{j})$

$\vec{r}=(4\hat{i}-\hat{k})+μ(2\hat{i}+3\hat{k})$

If the lines intersect, then for some value of λ and μ, we must have:

$(1+3\lambda)\hat{i}+(1-\lambda)\hat{j}-\hat{k}=(4+2\mu)\hat{i}+0\hat{j}+(3\mu-1)\hat{k}$

Now equate the coefficient of $\hat{i}, \hat{j},\hat{k}$we get

1 + 3λ = 4 + 2μ    ……(1)

1 – λ = 0                …..(2)

-1 = -1 +3μ           …..(3)

On solving the equation, we get

λ = 1 and μ = 0.

Now, substituting the values in eq(1), we get

1 + 3(1) = 4 + 2(0)

4 = 4

LHS = RHS 

Thus, the coordinates of the point of intersection of the two lines are (4, 0, -1).

问题 6. 确定以下几对线是否相交：

（一世） $\vec{r}=(\hat{i}-\hat{j})+\lambda( 2\hat{i}+\hat{k})$和$\vec{r}=(2\hat{i}-\hat{j})+\mu(\hat{i}-\hat{j}-\hat{k}).$

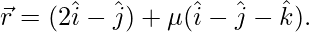
解决方案：

Given that:

$\vec{r}=(\hat{i}-\hat{j})+\lambda( 2\hat{i}+\hat{k})$

$\vec{r}=(2\hat{i}-\hat{j})+\mu(\hat{i}-\hat{j}-\hat{k}).$

If the lines intersect, then for some value of λ and μ, we must have:

$(1+2\lambda)\hat{i}-\hat{j}+\lambda\hat{k}=(2+\mu)\hat{i}+(-1+\mu)\hat{j}-\mu\hat{k}$

Now equate the coefficient of $\hat{i}, \hat{j},\hat{k}$we get

1 + 2λ = 2 + μ      …..(1)

-1 = -1 + μ           …..(2)

λ = -μ                 …..(3)

On solving the equations, we get

λ = 0 and μ = 0.

Now, substitute the values in eq(1), we get

1 + 2λ = 2 + μ

1 + 2(0) = 2 + 0

1 ≠ 2

LHS ≠ RHS 

Thus, the given lines do not intersect.

(二) $\frac{x-1}{2}=\frac{y+1}{3}=z$和$\frac{x+1}{5}=\frac{y-2}{1};z=2$

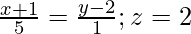
解决方案：

Given that the coordinates of any point on the line AB are 

$\frac{x-1}{2}=\frac{y+1}{3}=z=\lambda$

⇒ x = 2λ + 1, y = 3λ – 1, z = λ 

The coordinates of a general point on the second line are given by

$\frac{x+1}{5}=\frac{y-2}{1}=\mu;z=2$

⇒ x = 5μ – 1, y = μ + 2, z = 2

If the lines intersect, for some values of λ and μ, we must have:

2λ – 5μ = -2             ……(1)

3λ – μ = 3                ……(2)

λ = 2                        …..(3)

Solving this system of equations, we get

λ = 2 and μ = 3

On substituting the values in eq(3), we have

LHS = 2(2) – 5(3)

= -2 ≠ RHS

Thus, the given lines do not intersect each other.

㈢ $\frac{x-1}{3}=\frac{y-1}{-1}=\frac{z+1}{0}$和$\frac{x-4}{2}=\frac{y-0}{0}=\frac{z+1}{3}$

解决方案：

Given that the coordinates of any point on the line AB are 

$\frac{x-1}{3}=\frac{y-1}{-1}=\frac{z+1}{0}=\lambda$

⇒ x = λ, y = 2λ + 2, z = 3λ – 3

The coordinates of a general point on the second line are given by

$\frac{x-4}{2}=\frac{y-0}{0}=\frac{z+1}{3}=\mu$

⇒ x = 2μ + 4, y = 0, z = 3μ – 1

If the lines intersect, for some values of λ and μ, we must have:

λ – 2μ = 2            …….(1)

2λ – 3μ = 4         ……(2)

3λ – 4μ = 6         ……(3)

On solving this system of equations, we get

λ = 1 and μ = 0

On substituting the values in eq(3), we have

LHS = 3(1) – 2(0)

= 3 = RHS

Thus, the given lines intersect at (4, 0, -1).

(四) 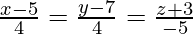$\frac{x-5}{4}=\frac{y-7}{4}=\frac{z+3}{-5}$和$\frac{x-8}{7}=\frac{y-4}{1}=\frac{z-5}{3}$

解决方案：

Given that the coordinates of any point on the line AB are 

$\frac{x-5}{4}=\frac{y-7}{4}=\frac{z+3}{-5}=\lambda$

⇒ x = 4λ + 5, y = 4λ + 7, z = -5λ – 3

The coordinates of a general point on the second line are given by:

$\frac{x-8}{7}=\frac{y-4}{1}=\frac{z-5}{3}=\mu$

⇒ x = 7μ + 8, y = μ + 4, z = 3μ + 5

If the lines intersect, for some values of λ and μ, we must have:

4λ – 7μ = 3            …….(1)

4λ – μ = -3            ……(2)

5λ + 3μ = -8        ……(3)

On solving this system of equations, we get

λ = -1 and μ = -1

On substituting the values in eq(3), we have

LHS = 5(-1) – 3(-1)

= -8 = RHS

Thus, the given lines intersect at (1, 3, 2).

问题 7. 显示线条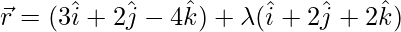$\vec{r}=(3\hat{i}+2\hat{j}-4\hat{k})+\lambda( \hat{i}+2\hat{j}+2\hat{k})$和$\vec{r}=(5\hat{i}-2\hat{j})+\mu(3\hat{i}+2\hat{j}+6\hat{k})$相交。因此，找到它们的交点。

解决方案：

Given that,

$\vec{r}=(3\hat{i}+2\hat{j}-4\hat{k})+\lambda( \hat{i}+2\hat{j}+2\hat{k})$

$\vec{r}=(5\hat{i}-2\hat{j})+\mu(3\hat{i}+2\hat{j}+6\hat{k})$

If the lines intersect, then for some value of λ and μ, we must have:

$(3+\lambda)\hat{i}-\hat{j}+(2+2\lambda)\hat{j}+(2\lambda-4)\hat{k}=(2+\mu)\hat{i}+(-1+\mu)\hat{j}-\mu\hat{k}$

Now equate the coefficient of $\hat{i}, \hat{j},\hat{k}$we get

3 + λ = 5 + 3μ       ……..(1)

2 + 2λ = -2 + 2μ   ……..(2)

2λ – 4 = 6μ           ……..(3)

Solving the equation, we have:

λ = -4 and μ = -2.

On substituting the values, we get

LHS = 2(-4) – 4 

= -12

RHS = 6(-2)

= -12

Thus, the given lines intersect at point(-1, -6, -12).