第 12 课 RD Sharma 解决方案 – 第 28 章空间直线 – 练习 28.2 |设置 1
问题 1. 证明方向余弦为 12/13、-3/13、-4/13 的三条线; 4/13、12/13、3/13; 3/13, – 4/13, 12/13 相互垂直。
解决方案:
The direction cosines of the three lines are
l1 = 12/13, m1 = -3/13, n1 = -4/13
l2 = 4/13, m2 = 12/13, n2 = 3/13
l3 = 3/13, m3 = -4/13, n3 = 12/13
So, l1 l2 + m1 m2 + n1 n2 =![]() = 0
= 0
Also,
l2 l3 + m2 m3 + n2 n3 =![]() = 0
= 0
l1 l3 + m1 m3 + n1 n3 =![]() = 0
= 0
Therefore, the given lines are perpendicular to each other.
Hence proved.
问题 2. 证明通过点 (1, -1, 2) 和 (3, 4, -2) 的线垂直于通过点 (0, 3, 2) 和 (3, 5, 6) 的线。
解决方案:
We have,
![]() is passing through the points (1, -1, 2) and (3, 4, -2).
is passing through the points (1, -1, 2) and (3, 4, -2).
Also,![]() is passing through the points (0, 3, 2) and (3, 5, 6).
is passing through the points (0, 3, 2) and (3, 5, 6).
Then,
![]()
![]()
Now,
![]()
= 6 + 10 – 16
= 0
Therefore, the given lines are perpendicular to each other.
Hence proved.
问题 3. 证明通过点 (4, 7, 8) 和 (2, 3, 4) 的线平行于通过点 (-1, -2, 1) 和 (1, 2, 5) 的线)。
解决方案:
Equations of lines passing through the points (x1, y1, z1) and (x2, y2, z2) are given by
![]()
So, the equation of a line passing through (4, 7, 8) and (2, 3, 4) is
![]()
![]()
Also, the equation of the line passing through the points ( -1, -2,1) and (1, 2, 5) is
![]()
![]()
We know that two lines are parallel if,
![]()
And the Cartesian equations of the two lines are given by,
![]()
![]()
So, we get,
![]()
Therefore, the given lines are parallel to each other.
Hence proved.
问题 4. 求通过点 (-2, 4, -5) 并平行于由下式给出的线的直线的笛卡尔方程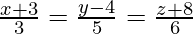 .
.
解决方案:
We know that the cartesian equation of a line passing through a point with position vector![]() and parallel to the vector
and parallel to the vector![]() is given by,
is given by,
![]()
Here,
![]()
![]()
The cartesian equation of the required line is,
![]()
=>![]()
问题 5. 显示线条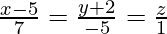 和
和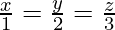 是相互垂直的。
是相互垂直的。
解决方案:
We have
![]()
And also,
![]()
These equations can be re-written as,
![]() . . . . (1)
. . . . (1)
![]() . . . . (2)
. . . . (2)
Therefore, the vector parallel to line (1) is given by,
![]()
And the vector parallel to line (2) is given by,
![]()
Now,
![]()
= 7 – 10 + 3
= 0
Therefore, the given two lines are perpendicular to each other.
Hence proved.
问题 6. 证明连接原点和点 (2, 1, 1) 的线垂直于由点 (3, 5, -1) 和 (4, 3, -1) 确定的线。
解决方案:
The direction ratios of the line joining the origin to the point (2, 1, 1) are 2, 1, 1.
Let![]()
The direction ratios of the line joining the points (3, 5, -1) and (4, 3, -1) are 1, -2, 0.
Let![]()
Now,
![]()
= 2 – 2 + 0
= 0
So, we get![]() .
.
Therefore, the two lines joining the given points are perpendicular to each other.
Hence proved.
问题 7. 求一条平行于 x 轴并通过原点的直线方程。
解决方案:
The direction ratios of the line parallel to x-axis are proportional to 1, 0, 0.
Equation of the line passing through the origin (0, 0, 0) and parallel to x-axis is
![]()
=>![]()
问题 8. 求以下一对直线之间的夹角:
(一世) ![]() 和
和![]()
解决方案:
We have,
![]()
And also,
![]()
Let![]() and
and![]() be vectors parallel to the given lines .
be vectors parallel to the given lines .
Now,
![]()
![]()
If θ is the angle between the given lines, then
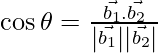
=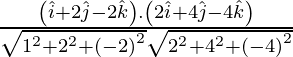
=![]()
= 1
As cos θ = 1
=> θ = 0°
Therefore, the angle between two lines is 0°.
(二) ![]() 和
和![]()
解决方案:
We have,
![]()
And also,
![]()
Let![]() and
and![]() be vectors parallel to the given lines .
be vectors parallel to the given lines .
Now,
![]()
![]()
If θ is the angle between the given line, then
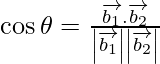
=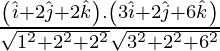
=![]()
= 19/21
As cos θ = 19/21
=> θ = cos-1 (19/21)
Therefore, the angle between two lines is cos-1 (19/21).
㈢ ![]() 和
和![]()
解决方案:
We have,
![]()
And also,
![]()
Let![]() and
and![]() be vector parallel to the given line.
be vector parallel to the given line.
Now,
![]()
![]()
If θ is the angle between the given line, then
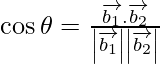
=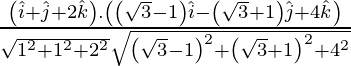
=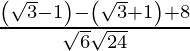
= 6/12
= 1/2
As cos θ = 1/2
=> θ = π/3
Therefore, the angle between two lines is π/3.
问题 9. 求下列一对直线之间的夹角:
(一世) ![]() 和
和![]()
解决方案:
We have,
![]()
And also,
![]()
Let,![]() and
and![]() be vectors parallel to the given line.
be vectors parallel to the given line.
![]()
![]()
If θ is the angle between the given line, then
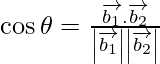
=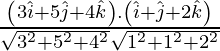
=![]()
= 8/5√3
As cos θ = 8/5√3
=> θ = cos-1 (8/5√3)
Therefore, the angle between two lines is cos-1 (8/5√3).
(二) ![]() 和
和![]()
解决方案:
We have,
![]()
And also,
![]()
Let![]() and
and![]() be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
![]()
![]()
If θ is the angle between the given lines, then
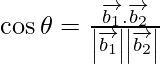
=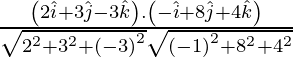
=![]()
=![]()
As cos θ =![]()
=> θ =![]()
Therefore, the angle between two lines is![]() .
.
㈢ ![]() 和
和![]()
解决方案:
We have,
![]()
And also,
![]()
The equation of the given line can be re-written as
![]()
![]()
Let![]() and
and![]() be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
![]()
![]()
If θ is the angle between the given lines, then
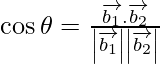
=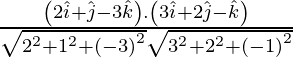
=![]()
= 11/14
As cos θ = 11/14
=> θ = cos-1 (11/14)
Therefore, the angle between two lines is cos-1 (11/14).
(四) ![]() 和
和![]()
解决方案:
We have,
![]()
And also,
![]()
The equations of the given lines can be re-written as
![]()
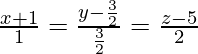
Let![]() and
and![]() be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
![]()
![]()
If θ is the angle between the given lines, then
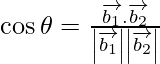
=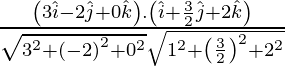
=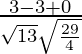
= 0
As cos θ = 0
=> θ = π/2
Therefore, the angle between two lines is π/2.
(五) ![]() 和
和![]()
解决方案:
We have,
![]()
And also,
![]()
The equations of the given lines can be re-written as,
![]()
![]()
Let![]() and
and![]() be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
![]()
![]()
If θ is the angle between the given lines, then
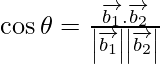
=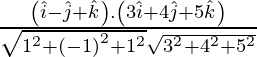
=![]()
= 4/5√6
As cos θ = 4/5√6
=> θ = cos-1 (4/5√6)
Therefore, the angle between two lines is cos-1 (4/5√6).
(六) ![]() 和
和![]()
解决方案:
We have,
![]()
And also,
![]()
The equations of the given lines can be re-written as
![]()
![]()
Let![]() and
and![]() be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
![]()
![]()
If θ is the angle between the given lines, then
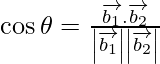
=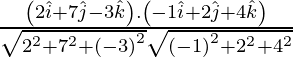
=![]()
= 0
As cos θ = 0
=> θ = π/2
Therefore, the angle between two lines is π/2.
问题 10. 求方向比与以下成比例的线对之间的角度:
(i) 5、-12、13 和 -3、4、5
解决方案:
We have pairs of lines with direction ratios proportional to 5, −12, 13 and −3, 4, 5.
Let![]() and
and![]() be vectors parallel to the two given lines.
be vectors parallel to the two given lines.
Then, the angle between the two given lines is same as the angle between![]() and
and![]() .
.
Now,
The vector parallel to the line having direction ratios proportional to 5, – 12, 13 is,
![]()
And the vector parallel to the line having direction ratios proportional to -3, 4, 5 is,
![]()
Let θ be the angle between the lines.
Now,
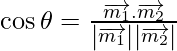
=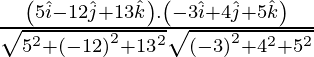
=![]()
= 1/65
As cos θ = 1/65
=> θ = cos-1 (1/65)
Therefore, the angle between two lines is cos-1 (1/65).
(ii) 2、2、1 和 4、1、8
解决方案:
We have pairs of lines with direction ratios proportional to 2, 2, 1 and 4, 1, 8.
Let![]() and
and![]() be vectors parallel to the given two lines.
be vectors parallel to the given two lines.
Then, the angle between the lines is same as the angle between![]() and
and![]() .
.
Now,
The vector parallel to the line having direction ratios proportional to 2, 2, 1 is,
![]()
And the vector parallel to the line having direction ratios proportional to 4, 1, 8 is,
![]()
Let θ be the angle between the lines.
Now,
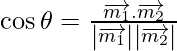
=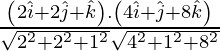
=![]()
= 2/3
As cos θ = 2/3
=> θ = cos-1 (2/3)
Therefore, the angle between two lines is cos-1 (2/3).
(iii) 1、2、-2 和 -2、2、1
解决方案:
We have pairs of lines with direction ratios proportional to 1, 2, −2 and −2, 2, 1.
Let![]() and
and![]() be vectors parallel to the two given lines.
be vectors parallel to the two given lines.
Then, the angle between the two given lines is same as the angle between![]() and
and![]() .
.
Now,
The vector parallel to the line having direction ratios proportional to 1, 2, – 2 is,
![]()
And the vector parallel to the line having direction ratios proportional to -2, 2, 1 is,
![]()
Let θ be the angle between the lines.
Now,
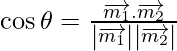
=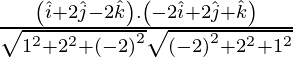
=![]()
= 0
As cos θ = 0
=> θ = π/2
Therefore, the angle between two lines is π/2.
(iv) a、b、c 和 b-c、c-a、a-b
解决方案:
We have pairs of lines with direction ratios proportional to a, b, c and b − c, c − a, a − b.
Let![]() and
and![]() be vectors parallel to the given two lines.
be vectors parallel to the given two lines.
Then, the angle between the two lines is same as the angle between![]() and
and![]() .
.
Now,
The vector parallel to the line having direction ratios proportional to a, b, c is,
![]()
And the vector parallel to the line having direction ratios proportional to b – c, c – a, a – b is,
![]()
Let θ be the angle between the lines.
Now,
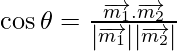
=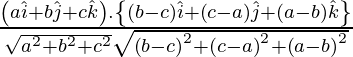
=![]()
= 0
As cos θ = 0
=> θ = π/2
Therefore, the angle between two lines is π/2.
问题 11. 求两条线之间的夹角,其中一条的方向比为 2, 2, 1,而另一条是通过连接点 (3, 1, 4) 和 (7, 2, 12) 得到的。
解决方案:
The direction ratios of the line joining the points (3, 1, 4) and (7, 2, 12) are proportional to 4, 1, 8.
Let![]() and
and![]() be vectors parallel to the lines having direction ratios proportional to 2, 2, 1 and 4, 1, 8.
be vectors parallel to the lines having direction ratios proportional to 2, 2, 1 and 4, 1, 8.
Now,
![]()
![]()
If θ is the angle between the given lines, then
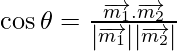
=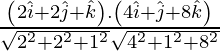
=![]()
= 2/3
As cos θ = 2/3
=> θ = cos-1 (2/3)
Therefore, the angle between two lines is cos-1 (2/3).
问题 12. 求通过点 (1, 2, -4) 并平行于直线的直线方程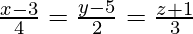 .
.
解决方案:
The direction ratios of the line parallel to line![]() are proportional to 4, 2, 3.
are proportional to 4, 2, 3.
Equation of the required line passing through the point (1, 2,-4) having direction ratios proportional to 4, 2, 3 is
![]()
=>![]()