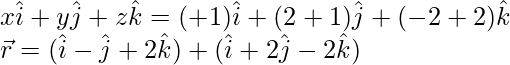第12类RD Sharma解决方案–第28章空间中的直线–练习28.1 |套装1

问题1.找到通过点(5，2，-4)且与向量平行的直线的向量和笛卡尔方程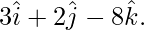$3\hat{i}+2\hat{j}-8\hat{k}.$

解决方案：

As we know that the vector equation of a line is;

$\vec{r}=\vec{a}+\lambda\vec{b}$

Thus, the Cartesian equation of a line is;

$\frac{x-x_1}{a_1}=\frac{y-y_1}{a_2}=\frac{x-x_3}{a_3}$

After applying the above formulas;

The vector equation of the line is;

$\vec{r}=(5\hat{i}+2\hat{j}-4\hat{k})+\lambda(3\hat{i}+2\hat{j}-8\hat{k})$

The Cartesian equation of a line is;

$\frac{x-5}{3}=\frac{y-2}{2}=\frac{z+4}{-8}$

问题2。找到通过点(-1，0，2)和(3，4，6)的直线的矢量方程。

解决方案：

Given:

Here, the direction ratios of the line are;

(3 + 1, 4 – 0, 6 – 2) = (4, 4, 4)

Thus, the given line passes through

(-1, 0, 2)

As we know that the vector equation of a line is given as;

$\vec{r}=\vec{a}+\lambda\vec{b}$

Thus, substitute values

Hence, we get

$\vec{r}=\vec{a}+\lambda\vec{b}\\ \vec{r}=(-\vec{i}+0\vec{j}+2\vec{k})+\lambda(4\vec{i}+4\vec{j}+4\vec{k})$

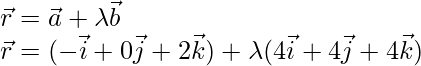
Therefore,

Vector equation of the line is;

$\vec{r}=(-\vec{i}+0\vec{j}+2\vec{k})+\lambda(4\vec{i}+4\vec{j}+4\vec{k})$

问题3.细化与向量平行的线的向量方程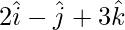$2\hat{i}-\hat{j}+3\hat{k}$并通过点(5，-2，4)，并将其简化为笛卡尔形式。

解决方案：

Consider,

The vector equation of line passing through a fixed point vector a and parallel to vector b is shown as;

$\vec{r}=\vec{a}+\lambda\vec{b}$

Here, λ is scalar

$\vec{b}=2\hat{i}-\hat{j}+3\hat{k}$and$\vec{a}=5\hat{i}-2\hat{j}+4\hat{k}$

The equation of the required line is;

$\vec{r}=\vec{a}+\lambda\vec{b}\\ \vec{r}=(5\hat{i}-2\hat{j}+4\hat{k})+\lambda(2\hat{i}-\hat{j}+3\hat{k})$

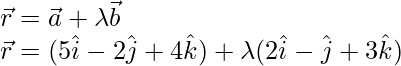
Now substitute the value of r here

$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$

Thus, we get

$(x\hat{i}+y\hat{j}+z\hat{k})=(5+2\lambda)\hat{i}+(-2-\lambda)\hat{j}+(4+3\lambda)\hat{k}$

Now compare the coefficients of vector

x = 5 + 2λ,y = -2 – λ,z = 4 + 3λ

After equating to λ,

We will have

$\frac{x-5}{2}=λ ,\ \ \frac{y+2}{-0}=λ ,\ \ \frac{z-4}{3}=λ$

Therefore,

The Cartesian form of equation of the line is;

$\frac{x-5}{2} =\ \ \frac{y+2}{-0} =\ \ \frac{z-4}{3}$

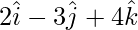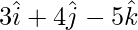问题4.一条穿过带有位置矢量的点的线$2\hat{i}-3\hat{j}+4\hat{k}$并朝着$3\hat{i}+4\hat{j}-5\hat{k}$ 。查找矢量和笛卡尔形式的直线方程。

解决方案：

Consider,

The vector equation of line passing through a fixed point vector a and parallel to vector b is shown as;

$\vec{r}=\vec{a}+\lambda\vec{b}$

Here, λ is scalar

$\vec{a}=2\hat{i}-3\hat{j}+4\hat{k}$and$\vec{b}=3\hat{i}+4\hat{j}-5\hat{k}$

The equation of the required line is;

$\vec{r}=\vec{a}+\lambda\vec{b}\\ \vec{r}=(2\hat{i}-3\hat{j}+4\hat{k})+\lambda(3\hat{i}+4\hat{j}-5\hat{k})$

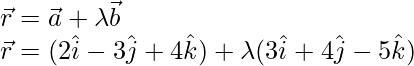
Now substitute the value of r here

$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$

Thus, we get

$(x\hat{i}+y\hat{j}+z\hat{k})=(2+3\lambda)\hat{i}+(-3+4\lambda)\hat{j}+(4-5\lambda)\hat{k}$

Now compare the coefficients of vector

x = 2 + 3λ,y = -3 + 4λ,z = 4 – 5λ

After equating to λ,

We will have

$\frac{x-2}{3}=λ ,\ \ \frac{y+3}{4}=λ ,\ \ \frac{z-4}{-5}=λ$

Therefore,

The Cartesian form of equation of the line is;

$\frac{x-2}{3} =\ \ \frac{y+3}{4} =\ \ \frac{z-4}{-5}$

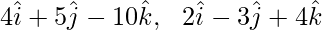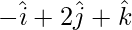问题5. ABCD是平行四边形。点A，B和C的位置向量分别是$4\hat{i}+5\hat{j}-10\hat{k},\ \ 2\hat{i}-3\hat{j}+4\hat{k}$和$-\hat{i}+2\hat{j}+\hat{k}$ 。找到线BD的矢量方程。也可以将其简化为笛卡尔形式。

解决方案：

Given: ABCD is a parallelogram.

Consider: AC and BD bisects each other at point O.

Thus,

Position vector of point O =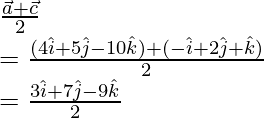$\frac{\vec{a}+\vec{c}}{2}\\ =\frac{(4\hat{i}+5\hat{j}-10\hat{k})+(-\hat{i}+2\hat{j}+\hat{k})}{2}\\ =\frac{3\hat{i}+7\hat{j}-9\hat{k}}{2}$

Now, Consider position vector of point O and B are represented by

$\vec{o}$and$\vec{b}$

Thus,

Equation of the line BD is the line passing through O and B is given by

$\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})$[Since equation of the line passing through two points$\vec{a}$and$\vec{b}$]

$\vec{r}=\vec{a}+\lambda(\vec{o}-\vec{b})\\ (2\hat{i}-3\hat{j}+4\hat{k})+\lambda\left(\frac{3\hat{i}+7\hat{j}-9\hat{k}}{2}-2\hat{i}-3\hat{j}+4\hat{k}\right)\\ \vec{r}=(2\hat{i}-3\hat{j}+4\hat{k})+\lambda(3\hat{i}+7\hat{j}-9\hat{k}-4\hat{i}+6\hat{j}-8\hat{k})\\ \vec{r}=(2\hat{i}-3\hat{j}+4\hat{k})+\lambda(-\hat{i}+13\hat{j}-17\hat{k})$

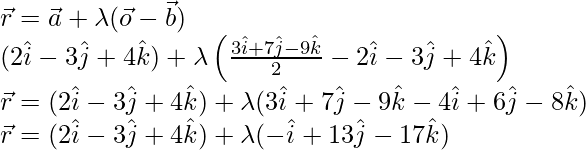
Now, compare the coefficients of vector i, j, R

x = 2 – λ, y = -3 – 13λ, z = 4 – 17λ

After equating to λ,

We will have

$\frac{x-2}{-1}=λ ,\ \ \frac{y+3}{13}=λ ,\ \ \frac{z-4}{-17}=λ$

Therefore,

The Cartesian form of equation of the line is;

$\frac{x-2}{-1} =\ \ \frac{y+3}{13} =\ \ \frac{z-4}{-17}$

问题6：找到矢量形式以及笛卡尔形式，即通过点A(1、2，-1)和B(2、1、1)的线方程。

解决方案：

We know that, equation of line passing though two points (x₁, y₁ ,z₁) and (x₂, y₂, z₂) is

$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\ \ \ \ \ \ \ ....(i)\\$

Here,

(x₁, y₁, z₁) = A(1, 2, -1)

(x₂, y₂ ,z₂) = B(2, 1, 1)

Using equation (i), equation of line AB,

$\frac{x-1}{2-1}=\frac{y-2}{1-2}=\frac{z+1}{1+1}\\ \frac{x-1}{1}=\frac{y-2}{-1}=\frac{z+1}{2}=\lambda\ (assume)$

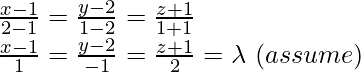
x = λ + 1, y = -λ + 2, z = 2λ – 1

Vector form of equation of line AB is,

$x\hat{i}+y\hat{j}+z\hat{k}=(\lambda+1)\hat{i}+(-\lambda+2)\hat{j}+(2\lambda-1)\hat{k}\\ \vec{r}=(\hat{i}+2\hat{j}-\hat{k})+\lambda(\hat{i}-\hat{j}+2\hat{k})$

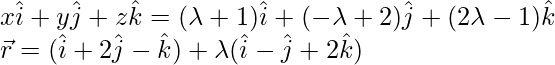
问题7.找到通过点(1、2、3)并平行于矢量的直线的矢量方程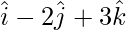$\hat{i}-2\hat{j}+3\hat{k}$ 。简化笛卡尔形式的相应方程式。

解决方案：

We know that vector equation of a line passing through$\vec{a}$and parallel to the vector$\vec{b}$is given by,

$\vec{r}=\vec{a}+\lambda\vec{b}$

Here,

$\vec{a}=\hat{i}+2\hat{j}+3\hat{k}$and$\vec{b}=\hat{i}-2\hat{j}+3\hat{k}$

So, required vector equation of line is,

$\vec{r}=(\hat{i}+2\hat{j}+3\hat{k})+\lambda(\hat{i}-2\hat{j}+3\hat{k})$

Now,

$(x\hat{i}+y\hat{j}+z\hat{k})=(1+\lambda)\hat{i}+(2-2\lambda)\hat{j}+(3+3\lambda)\hat{k}$

Equating the coefficients of$\hat{i},\ \hat{j},\ \hat{k}$

x = 1 + λ, y = 2 – 2λ, z = 3 + 3λ

x – 1 = λ,$\frac{y-2}{2}=λ,\ \frac{z-3}{3}=λ$

So, required equation of line is Cartesian form,

$\frac{x-1}{1}=\frac{y-2}{-2}=\frac{z-3}{3}$

问题8.找到经过(2，-1，1)并平行于方程为的线的向量方程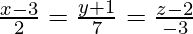$\frac{x-3}{2}=\frac{y+1}{7}=\frac{z-2}{-3}$

解决方案：

We know that, equation of a line passing through a point (x₁, y₁, z₁) and having direction ratios proportional to a, b, c is

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\ \ \ \ .....(i)$

Here,

(x₁, y₁, z₁) = (2, -1, 1) and

Given line$\frac{x-3}{2}=\frac{y+1}{7}=\frac{z-2}{-3}$is parallel to required line.

a = 2μ, b = 7μ, c = -3μ

So, equation of required line using equation (i)

$\frac{x-2}{2μ }=\frac{y+1}{7μ }=\frac{z-1}{-3μ }\\ \frac{x-2}{2}=\frac{y+1}{7}=\frac{z-1}{-3}=\lambda$

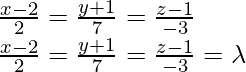
x = 2λ + 2, y = 7λ – 1, z = -3λ + 1

So,

$x\hat{i}+y\hat{j}+z\hat{k}=(2λ+2)\hat{i}+(7λ-1)\hat{j}+(-3λ+1)\hat{k}\\ \vec{r}=(2\hat{i}-\hat{j}+\hat{k})+λ(2\hat{i}+7\hat{j}-3\hat{k})$

问题9.线的笛卡尔方程为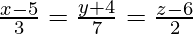$\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$ 。写出它的向量形式

解决方案：

The Cartesian equation of the line is

$\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$….(i)

The given line passes through the point (5, -4, 6). The position vector of this point is

$\vec{a}=5\hat{i}-4\hat{j}+6\hat{k}$

Also, the direction ratios of the given line are 3, 7 and 2.

This means that the line is in the direction of vector,

$\vec{b}=3\hat{i}+7\hat{j}+2\hat{k}$

It is known that the line through position vector$\vec{a}$and in the direction of the vector$\vec{b}$is given by the equation,

$\vec{r}=\vec{a}+\lambda \vec{b}, \lambda ∈R\\ \vec{r}=(5\hat{i}-4\hat{j}+6\hat{k})+\lambda(3\hat{i}+7\hat{j}+2\hat{k})$

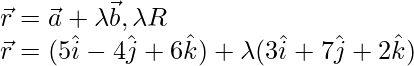
问题10.找到经过(1，-1，2)并平行于方程为的线的笛卡尔方程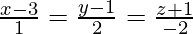$\frac{x-3}{1}=\frac{y-1}{2}=\frac{z+1}{-2}$ 。此外，简化以矢量形式获得的方程。

解决方案：

We know that, equation of a line passing through a point (x₁, y₁, z₁) and having direction ratios proportional to a, b, c is

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\ \ \ \ \ ......(i)$

Here,

(x₁, y₁, z₁) = (1, -1, 2) and

Given line$\frac{x-3}{1}=\frac{y-1}{2}=\frac{z+1}{-2}$is parallel to required line,

So,

a = μ, b = 2μ, c = -2μ

So, equation of required line using equation (i) is,

$\frac{x-1}{μ }=\frac{y+1}{2μ }=\frac{z-2}{-2μ }\\ \frac{x-1}{1}=\frac{y+1}{2}=\frac{z-2}{-2}=\lambda$

x = λ + 1, y = 2λ – 1, z = -2λ +2

So,

$x\hat{i}+y\hat{j}+z\hat{k}=(λ+1)\hat{i}+(2λ+1)\hat{j}+(-2λ+ 2)\hat{k}\\ \vec{r}=(\hat{i}-\hat{j}+2\hat{k})+λ(\hat{i}+2\hat{j}-2\hat{k})$