第 12 课 RD Sharma 解决方案 - 第 28 章空间直线 - 练习 28.5
问题 1. 求向量方程为的直线对之间的最短距离:
(一世) 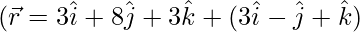 和
和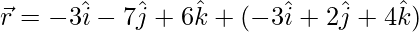
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 
Now, ![]()
= ![]()

= ![]()
= ![]()
![]()
= 36 + 225 + 9
= 270
![]()
= ![]()
= √270
On substituting the values in the formula, we have
SD = 270/√270
= √270
Shortest distance between the given pair of lines is 3√30 units.
(二)  和
和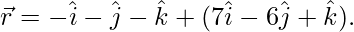
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 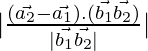
Now, ![]()
= ![]()
= ![]()
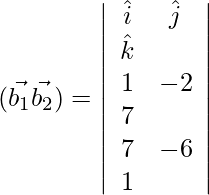
= ![]()
![]()
= – 16 × 32
= – 512
![]()
= ![]()
= ![]()
On substituting the values in the formula, we have
SD = ![]()
Shortest distance between the given pair of lines is ![]() units.
units.
㈢ 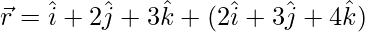 和
和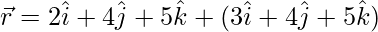
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 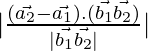
Now, ![]()
= ![]()
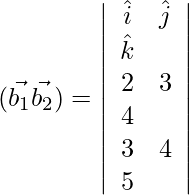
= ![]()
![]()
= 1
![]()
= ![]()
On substituting the values in the formula, we have
SD = ![]()
Shortest distance between the given pair of lines is 1/√6 units.
(四) 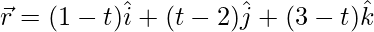 和
和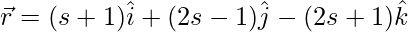
解决方案:
Above equations can be re-written as:
![]()
and, ![]()
As we know that the shortest distance between the lines ![]()
and ![]() is:
is:
D = 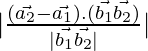
= 9/3√2
Shortest distance is 3/√2 units.
(五) 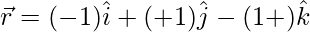 和
和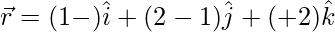
解决方案:
The given equations can be written as:
\![]() and
and ![]()
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 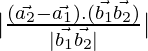
Now, ![]()
= 15
![]()
= 3√2
Thus, distance between the lines is ![]() units.
units.
(六) 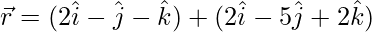 和
和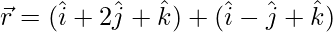
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D = 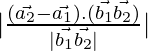
Now, ![]()
![]()
= 3√2
Substituting the values in the formula, we have
The distance between the lines is ![]() units.
units.
(七) 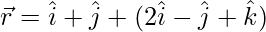 和
和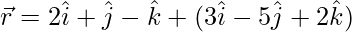
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 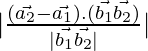
Now, ![]()
= 10
Substituting the values in the formula, we have:
The distance between the lines is 10/√59 units.
(八) 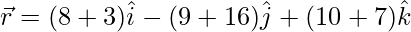 和
和
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 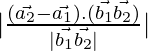
Now, ![]()
= 1176
![]()
= 84
Substituting the values in the formula, we have:
The distance between the lines is 1176/84 = 14 units.
问题 2. 找出笛卡尔方程为的直线对之间的最短距离:
(一世) 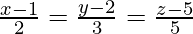 和
和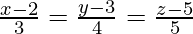
解决方案:
The given lines can be written as:
![]() and
and ![]()
![]()
= ![]()
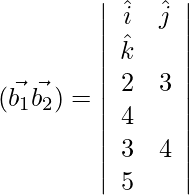
= ![]()
![]()
= –1
![]()
= √6
On substituting the values in the formula, we have:
SD = 1/√6 units.
(二) ![由 QuickLaTeX.com 渲染 \frac{x-1}{2}=\frac{y+1}{3}=z]() 和
和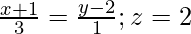
解决方案:
The given equations can also be written as:
![]() and \
and \![]()
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 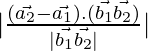
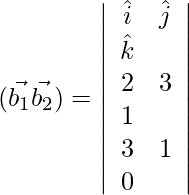
= ![]()
![]()
= 3
SD = 3/√59 units.
㈢ 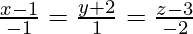 和
和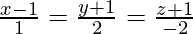
解决方案:
The given equations can be re-written as:
![]() and
and ![]()
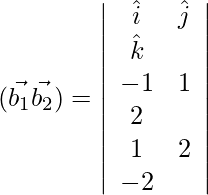
= √29
![]()
= 8
SD = 8/√29 units.
(四) 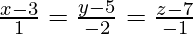 和
和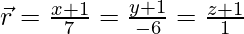
解决方案:
The given equations can be re-written as:
![]() and
and ![]()
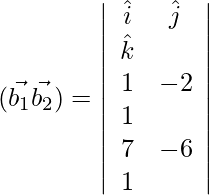
= ![]()
SD = 58/√29 units.
问题 3. 通过计算最短距离确定线对是否相交:
(一世) 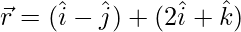 和
和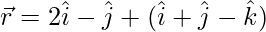
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 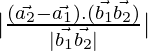
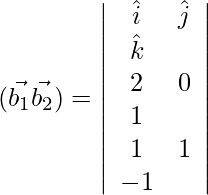
= ![]()
![]()
= –1
![]()
= √14
⇒ SD = 1/√14 units ≠ 0
Hence the given pair of lines does not intersect.
(二) 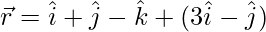 和
和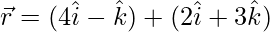
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 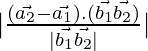

= ![]()
![]()
= 0
![]()
= √94
⇒ SD = 0/√94 units = 0
Hence the given pair of lines are intersecting.
㈢ ![由 QuickLaTeX.com 渲染 \frac{x-1}{2}=\frac{y+1}{3}=z]() 和
和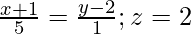
解决方案:
Given lines can be re-written as:
![]() and
and ![]()
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 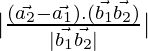
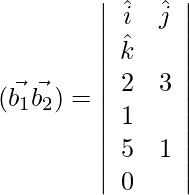
= ![]()
![]()
= −9
![]()
= √195
⇒ SD = 9/√195 units ≠ 0
Hence the given pair of lines does not intersect.
(四) 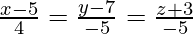 和
和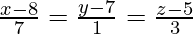
解决方案:
Given lines can be re-written as:
![]() and
and ![]()
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 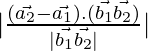
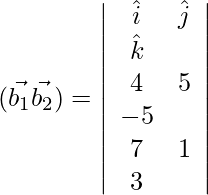
= ![]()
![]()
= 282
⇒ SD = 282/√3 units ≠ 0
Hence the given pair of lines does not intersect.
问题 4. 找出以下之间的最短距离:
(一世) 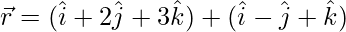 和
和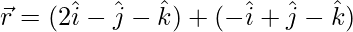
解决方案:
The second given line can be re-written as: ![]()
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 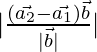
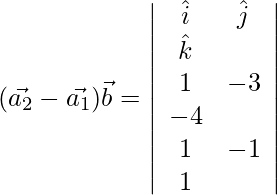
= ![]()
![]()
= ![]()
![]()
⇒ SD = ![]() units.
units.
(二) 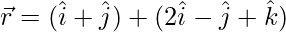 和
和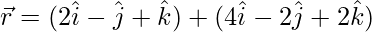
解决方案:
The second given line can be re-written as: ![]()
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 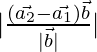
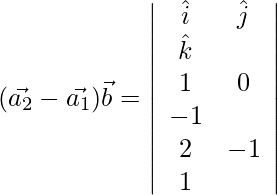
= ![]()
⇒ ![]()
= √11
![]()
⇒ SD = √11/√6 units.
问题 5. 找出连接下列顶点对的直线的方程,然后找出直线之间的最短距离:
(i) (0, 0, 0) 和 (1, 0, 2) (ii) (1, 3, 0) 和 (0, 3, 0)
解决方案:
Equation of the line passing through the vertices (0, 0, 0) and (1, 0, 2) is given by:
![]()
Similarly, the equation of the line passing through the vertices (1, 3, 0) and (0, 3, 0):
![]()
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 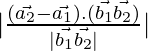
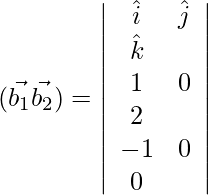
= ![]()
![]()
= −6
![]()
= 2
⇒ SD = |-6/2| = 3 units.
问题 6. 写出下列各行的向量方程,找出它们之间的最短距离:
解决方案:
The given equations can be written as:
![]() and
and ![]()
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 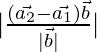
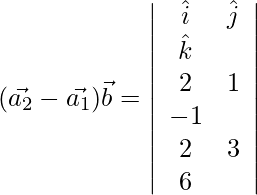
= ![]()
⇒ ![]()
= ![]()
\vec{|b|}= 7
⇒ SD = √293/7 units.
问题 7. 找出以下之间的最短距离:
(一世) 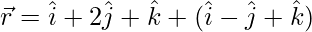 和
和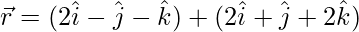
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 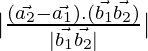
Now, ![]()
= ![]()
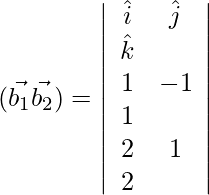
= ![]()
![]()
![]()
= 3√2
⇒ SD = 3/√2 units.
(二) 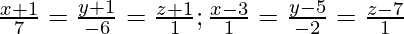
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 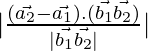
Now, ![]()
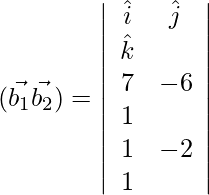
= ![]()
![]()
![]()
= √116
⇒ SD = 2√29 units.
㈢ 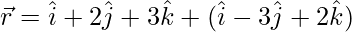 和
和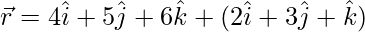
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 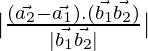
Now, ![]()
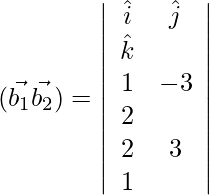
= ![]()
![]()
![]()
= √171
⇒ SD = 3√19 units.
(四) 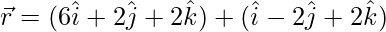 和
和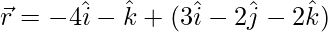
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 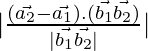
Now, ![]()
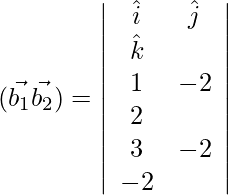
= ![]()
(\vec{a_2}-\vec{a_1}).(\vec{b_1}×\vec{b_2})=108
|\vec{b_1}×\vec{b_2}|=\sqrt{(-9)^2+(3)^2+(9)^2}
= 12
⇒ SD = 9 units.
问题 8. 求线之间的距离: 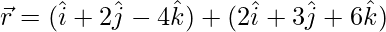 和
和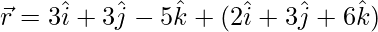
解决方案:
As we know that the shortest distance between the lines ![]() and
and ![]() is:
is:
D= 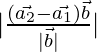
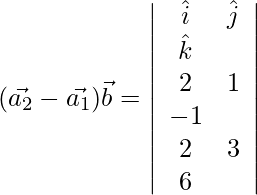
= ![]()
⇒ ![]()
= √293
![]()
⇒ SD = √293/7 units.