第12类RD Sharma解–第8章线性方程组的解–练习8.2

用矩阵法求解下列齐次线性方程组：

问题1

2x – y + z = 0

3x + 2y – z = 0

x + 4y + 3z = 0

解决方案：

Given

2x – y + z = 0

3x + 2y – z = 0

X + 4y + 3z = 0

The system can be written as

$\begin{bmatrix} 2 & -1 & 1\\ 3 & 2 & -1\\ 1 & 4 &3 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$

A X = 0

Now, |A| = 2(6 + 4) + 1(9 + 1) + 1(12 – 2)

|A| = 2(10) + 10 + 10

|A| = 40 ≠ 0

Since, |A|≠ 0, hence x = y = z = 0 is the only solution of this homogeneous equation.

问题2。

2x – y + 2z = 0

5x + 3y – z = 0

X + 5y – 5z = 0

解决方案：

Given 2x – y + 2z = 0

5x + 3y – z = 0

X + 5y – 5z = 0

$\begin{bmatrix} 2 & -1 & 2\\ 5 & 3 & -1\\ 1 & 5 & -5 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$

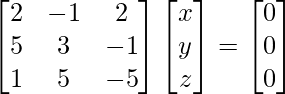
A X = 0

Now, |A| = 2(– 15 + 5) + 1(– 25 + 1) + 2(25 – 3)

|A| = – 20 – 24 + 44

|A| = 0

Thus, the system has infinite solutions

Let z = k

2x – y = – 2k

5x + 3y = k

$\begin{bmatrix} 2 & -1\\ 3 & 2 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} -2k\\ k \end{bmatrix}\\ AX=B\\ |A|=6+5=11\neq0 \ \ So,A^{-1}\ exist\\ Now\ adj\ A=\begin{bmatrix} 3&-5\\ 1&2 \end{bmatrix}^T=\begin{bmatrix} 3&1\\ -5&2 \end{bmatrix}\\ X=A^{-1}B=\frac{1}{|A|}(adjA)B=\frac{1}{11}\begin{bmatrix} 3&1\\ -5&2 \end{bmatrix}\begin{bmatrix} -2k\\ k\end{bmatrix}\\ X=\begin{bmatrix}\frac{-5k}{11}\\{\frac{12k}{11}}\end{bmatrix} \\Hence, X=\frac{-5k}{11},Y=\frac{12k}{11}and\ z=k$

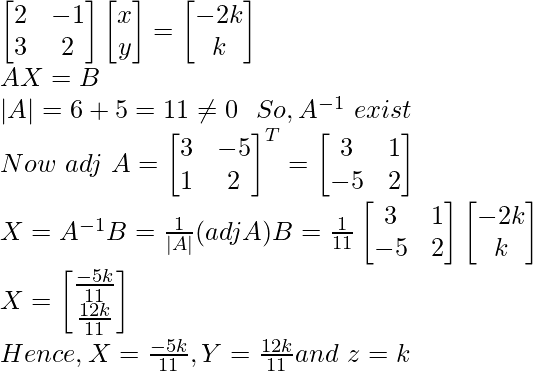
问题3。

3x – y + 2z = 0

4x + 3y + 3z = 0

5x + 7y + 4z = 0

解决方案：

Given: 

3x – y + 2z = 0

4x + 3y + 3z = 0

5x + 7y + 4z = 0

$\begin{bmatrix} 3 & -1 & 2\\ 4 & 3 & 3\\ 5 & 7 &4 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$

A X = 0

Now, |A| = 3(12 – 21) + 1(16 – 15) + 2(28 – 15)

|A| = – 27 + 1 + 26

|A| = 0

Hence, the system has infinite solutions

Let z = k

3x – y = – 2k

4x + 3y = – 3k

$\begin{bmatrix} 3 & -1\\ 4 & 3 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} -2k\\ -3k \end{bmatrix}\\ AX=B\\ |A|=9+4=13\neq0 \ \ So,A^{-1}\ exist\\ Now\ adj\ A=\begin{bmatrix} 3&-1\\ 4&3 \end{bmatrix}^T=\begin{bmatrix} 3&1\\ -4&3 \end{bmatrix}\\ X=A^{-1}B=\frac{1}{|A|}(adjA)B=\frac{1}{12}\begin{bmatrix} 3&1\\ -4&3 \end{bmatrix}\begin{bmatrix} -2k\\ -3k\end{bmatrix}\\ X=\begin{bmatrix}\frac{-9k}{13}\\{\frac{-k}{13}}\end{bmatrix}\\Hence, X=\frac{-9k}{13},Y=\frac{-k}{13}and\ z=k$

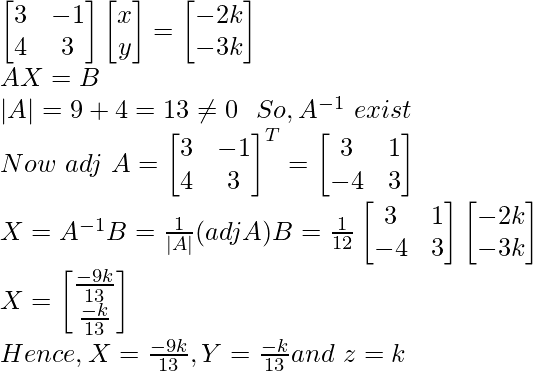
问题4。

x + y – 6z = 0

x – y + 2z = 0

– 3x + y + 2z = 0

解决方案：

Given: 

x + y – 6z = 0

x – y + 2z = 0

– 3x + y + 2z = 0

$\begin{bmatrix} 1 & 1 & -6\\ 1 & -1 & 2\\ -3 & 1 & 2 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$

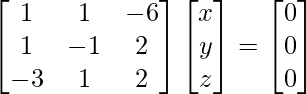
A X = 0

Now, |A| = 1(– 2 – 2) – 1(2 + 6) – 6(1 – 3)

|A| = – 4 – 8 + 12

|A| = 0

Hence, the system has infinite solutions

Let z = k

x + y = 6k

x – y = – 2k

$\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} 6k\\ -2k \end{bmatrix}\\ AX=B\\ |A|=-1-1=-2\neq0 \ \ So,A^{-1}\ exist\\ Now\ adj\ A=\begin{bmatrix} -1&-1\\ -1&1 \end{bmatrix}^T=\begin{bmatrix} -1&-1\\ -1&1 \end{bmatrix}\\ X=A^{-1}B=\frac{1}{|A|}(adjA)B=\frac{1}{-2}\begin{bmatrix} -1&-1\\ -1&1 \end{bmatrix}\begin{bmatrix} 6k\\ -2k\end{bmatrix}\\ X=\frac{1}{-2}\begin{bmatrix}-6k+2k\\-6k-2k\end{bmatrix}\\ X=\begin{bmatrix}-4k\\-8k\end{bmatrix}\\ Hence, X=2k,\ Y=4k\ and\ Z=k$

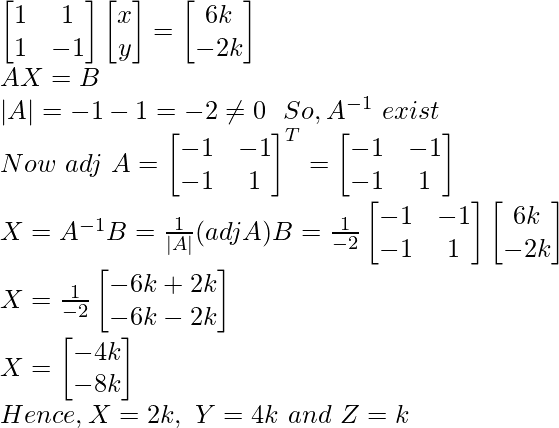
问题5.用矩阵法求解齐次线性方程组：

x + y + z = 0

x – y – 5z = 0

x + 2y + 4z = 0

解决方案：

Given:

x + y + z = 0

x – y – 5z = 0

x + 2y + 4z = 0

$\begin{bmatrix} 1 & 1 & 1\\ 1 & -1 & -5\\ 1 & 2 & 4 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$

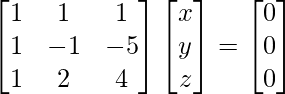
A X = 0

Now, |A| = 1(6) – 1(9) + 1(3)

|A| = 9 – 9

|A| = 0

Hence, the system has infinite solutions

Let z = k

x + y = –k

x – y = 5k

$\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} -k\\ 5k \end{bmatrix}\\ AX=B\\ |A|=-1-1=-2\neq0 \ \ So,A^{-1}\ exist\\ Now\ adj\ A=\begin{bmatrix} -1&-1\\ -1&1 \end{bmatrix}^T=\begin{bmatrix} -1&-1\\ -1&1 \end{bmatrix}\\ X=A^{-1}B=\frac{1}{|A|}(adjA)B=\frac{1}{-2}\begin{bmatrix} -1&-1\\ -1&1 \end{bmatrix}\begin{bmatrix} -k\\ 5k\end{bmatrix}\\ \begin{bmatrix}X\\Y\end{bmatrix}=\frac{1}{-2}\begin{bmatrix}k-5k\\k+5k\end{bmatrix}=\begin{bmatrix}2k\\-3k\end{bmatrix}\\ Hence, X=2k,\ Y=-3k\ and\ Z=k$

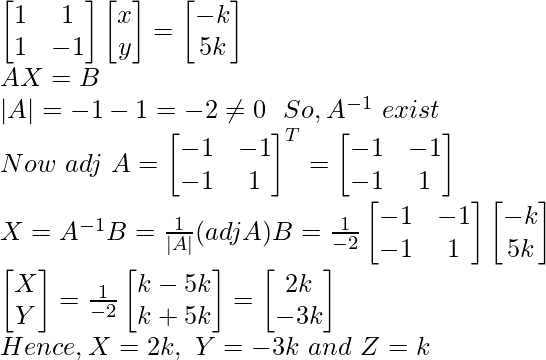
问题6.用矩阵法求解齐次线性方程组：

x + y – z = 0

x – 2y + z = 0

3x + 6y –5z = 0

解决方案：

Given:

x + y – z = 0

x – 2y + z = 0

3x + 6y –5z = 0

$\begin{bmatrix} 1 & 1 & -1\\ 1 & -2 & 1\\ 3 & 6 & -5 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$

A X = 0

Now, |A| = 1(4) – 1(–8) – 1(12)

|A| = 4 + 8  – 12

|A| = 0

Hence, the system has infinite solutions

Let z = k

x + y = –k

x – 2y = –k

$\begin{bmatrix} 1 & 1\\ 1 & -2 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} k\\ -k \end{bmatrix}\\ AX=B\\ |A|=-2\neq0 \ \ So,A^{-1}\ exist\\ Now\ adj\ A=\begin{bmatrix} -2&-1\\ -1&1 \end{bmatrix}^T=\begin{bmatrix} -2&-1\\ -1&1 \end{bmatrix}\\ X=A^{-1}B=\frac{1}{|A|}(adjA)B=\frac{1}{-3}\begin{bmatrix} -2&-1\\ -1&1 \end{bmatrix}\begin{bmatrix} k\\ -k\end{bmatrix}\\ =\frac{-1}{3}\begin{bmatrix}-2k+k\\-2k\end{bmatrix}\\=\frac{-1}{3}\begin{bmatrix}-k\\-2k\end{bmatrix}=\begin{bmatrix}\frac{k}{3}\\\frac{2k}{3}\end{bmatrix}\\ Hence, X=\frac{k}{3},\ Y=\frac{2k}{3}\ and\ Z=k$

问题7.用矩阵法求解齐次线性方程组：

3x + y – 2z = 0

x + y + z = 0

x – 2y + z = 0

解决方案：

Given:

3x + y – 2z = 0

x + y + z = 0

x – 2y + z =0

$\begin{bmatrix} 3 & 1 & -2\\ 1 & 1 & 1\\ 1 & -2 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$

A X = 0

Now, |A| = 3(3) – 1(0) – 2(–3)

|A| = 9 – 0  + 6

|A| = 15 ≠ 0,

Hence, the given system has only trivial solutions given by x = y = z = 0.

问题8.用矩阵法求解齐次线性方程组：

2x + 3y – z = 0

x – y – 2z = 0

3x + y + 3z = 0

解决方案：

Given:

2x + 3y – z =0

x – y – 2z = 0

3x + y + 3z = 0

$\begin{bmatrix} 2 & 3 & -1\\ 1 & -1 & -2\\ 3 & 1 & 3 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}$

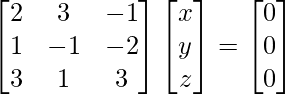
A X = 0

Now, |A| = 2(–3 + 2) – 3(3 + 6) – 1(4)

|A| = –2 – 27  – 4

|A| = –33 ≠ 0,

Hence, the given system has only trivial solutions given by x = y = z = 0.