第 12 类 RD Sharma 解——第 8 章联立线性方程组的解——练习 8.1 |设置 1
问题 1. 用矩阵法求解下列方程组:
(i) 5x + 7y + 2 = 0
4x + 6y + 3 = 0
解决方案:
The given system of equations can be written in matrix form as,
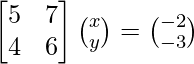
AX = B
Here,
A =  , X =
, X = ![]() and B =
and B = ![]()
Now,
|A| = 
= 30 – 28
= 2
The given system has a unique solution given by, X = A-1 B.
Let Cij be the cofactor of the elements aij in A.
C11 = (-1)1+1 (6) = 6, C12 = (-1)1+2 (4) = -4, C21 = -12+1 (7) = -7 and C22 = (-1)2+2 (5) = 5
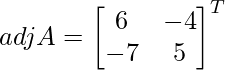
= 
A-1 = ![]()
A-1 = 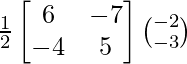
So, X = A-1 B
= 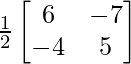
= ![]()
=> 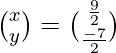
Therefore, x = 9/2 and y = -7/2.
(ii) 5x + 2y = 3
3x + 2y = 5
解决方案:
The given system of equations can be written in matrix form as,
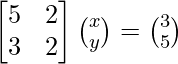
AX = B
Here,
A = 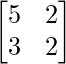 , X =
, X = ![]() and B =
and B = ![]()
Now,
|A| = 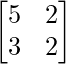
= 10 – 6
= 4
The given system has a unique solution given by, X = A-1 B
Let Cij be the cofactor of the elements aij in A.
C11 = -11+1 (2) = 2, C12 = (-1)1+2 (3) = – 3, C21 = (-1)2+1 (2) = – 2 and C22 = (-1)2+2 (5) = 5
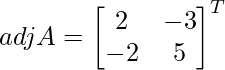
= 
A-1 = ![]()
= 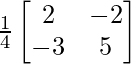
Now, X = A-1 B
= 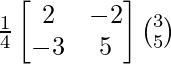
= ![]()
=> 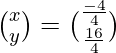
Therefore, x = – 1 and y = 4.
(iii) 3x + 4y - 5 = 0
x - y + 3 = 0
解决方案:
The given system of equations can be written in matrix form as,
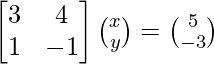
AX = B
Here,
A = 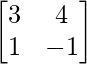 , X =
, X = ![]() and B =
and B = ![]()
Now,
|A| = 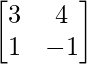
= – 3 – 4
= -7
So, the given system has a unique solution given by, X = A-1 B
Let Cij be the cofactors of the elements aij in A.
C11 = (-1)1+1 (1) = -1, C12 = (-1)1+2 (-1) = 1, C21 = (-1)2+1 (4) = -4 and C22 = (-1)2+2 (3) = 3
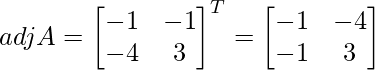
![]()
= 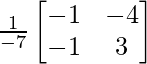
Now, X = A-1 B
= 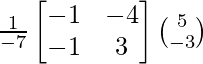
= ![]()
=> 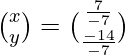
Therefore, x = -1 and y = 2.
(iv) 3x + y = 19
3x - y = 23
解决方案:
The given system of equations can be written in matrix form as,
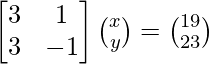
AX = B
Here,
A = 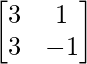 , X =
, X = ![]() and B =
and B = ![]()
Now,
|A| = 
= – 3 – 3
= -6
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
C11 = (-1)1+1 (-1) = -1, C12 = (-1)1+2 (3) = -3, C21 = (-1)2+1 (1) = -4 and C22 = (-1)2+2 (3) = 3
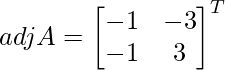
= 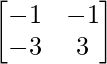
![]()
= 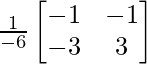
Now, X = A-1 B
= 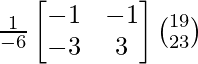
= ![]()
=> 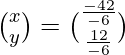
Therefore, x = 7 and y = -2.
(v) 3x + 7y = 4
x + 2y = -1
解决方案:
The given system of equations can be written in matrix form as,
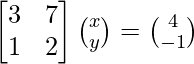
AX = B
Here,
A =  , X =
, X = ![]() and B =
and B = ![]()
Now,
|A| = 
= 6 – 7
= -1
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
C11 = (-1)1+1 (2) = 2, C12 = (-1)1+2 (1) = -1, C21 = (-1)2+1 (7) = -7 and C22 = (-1)2+2 (3) = 3
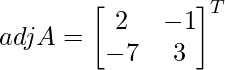
= 
![]()
= 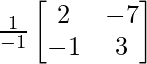
X = A-1 B
= 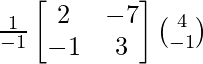
= ![]()
=> 
Therefore x = – 15 and y = 7.
(vi) 3x + y = 7
5x + 3y = 12
解决方案:
The given system of equations can be written in matrix form as,

AX = B
Here,
A = 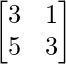 , X =
, X = ![]() and B =
and B = ![]()
Now,
|A| = 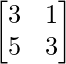
= 9 – 5
= 4
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
C11 = (-1)1+1 (3) = 3, C12 = (-1)1+2 (5) = -5, C21 = (-1)2+1 (1) = -1 and C22 = (-1)2+2 (3) = 3
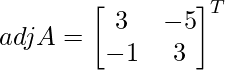
= 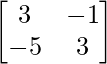
![]()
= 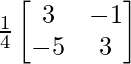
X = A-1 B
= 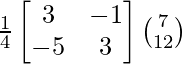
= ![]()
=> 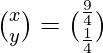
Therefore x = 9/4 and y = 1/4.
问题 2. 用矩阵法求解下列方程组:
(i) x + y - z = 3
2x + 3y + z = 10
3x - y - 7z = 1
解决方案:
A = 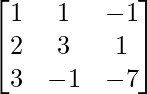
|A| = 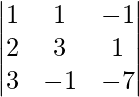
= 1 (- 21 + 1) – 1(-14 – 3) – 1(-2 – 9)
= – 20 + 17 + 11
= 8
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactor of the elements aij in A.
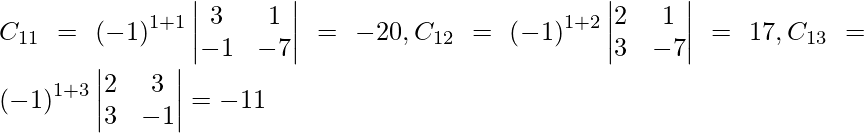
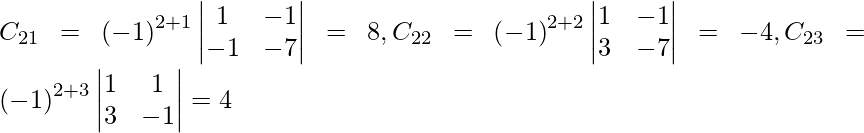
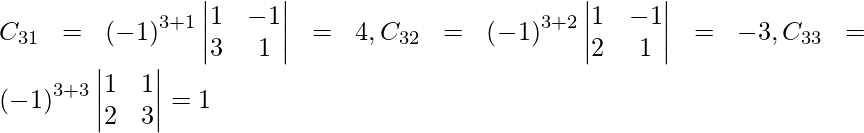
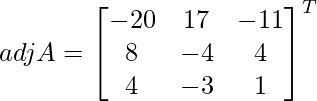
= 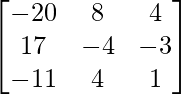
![]()
= 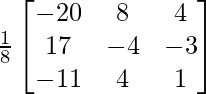
X = A-1 B
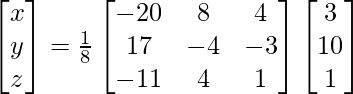
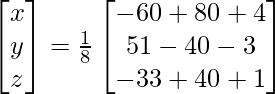
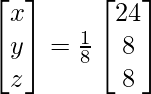
=> x = 24/8, y = 8/8 and z = 8/8
Therefore, x = 3, y = 1 and z = 1.
(ii) x + y + z = 3
2x - y + z = - 1
2x + y - 3z = - 9
解决方案:
A = 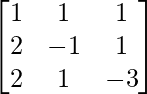
|A| = 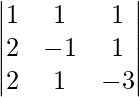
= 1 (3 – 1) – 1 (-6 – 2) + 1 (2 + 2)
= 2 + 8 + 4
= 14
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
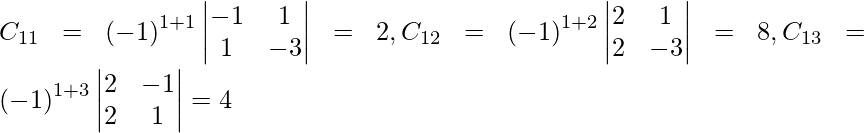
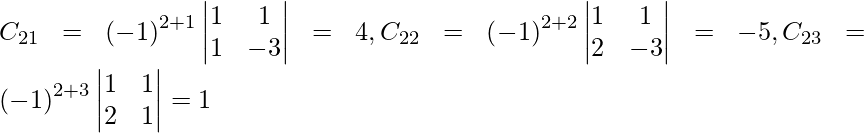
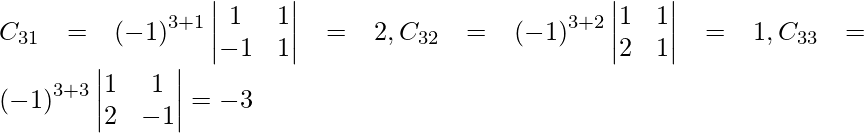
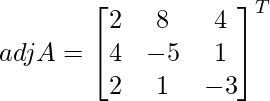
= 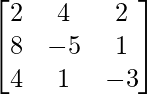
![]()
= 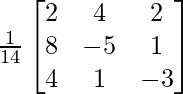
Now, X = A-1 B
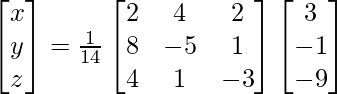
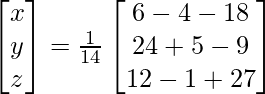
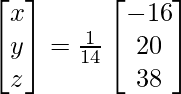
=> x = -16/14, y = 20/14 and z = 38/14
Therefore, x = -8/7, y = 10/7 and z = 19/7.
(iii) 6x - 12y + 25z = 4
4x + 15y - 20z = 3
2x + 18y + 15z = 10
解决方案:
A = 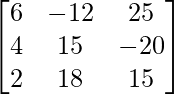
|A| = 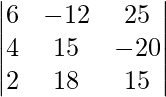
= 6 (225 + 360) + 12 (60 + 40) + 25 (72 – 30)
= 3510 + 1200 + 1050
= 5760
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
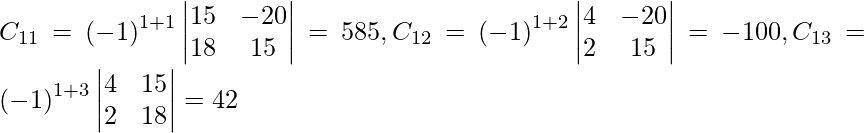
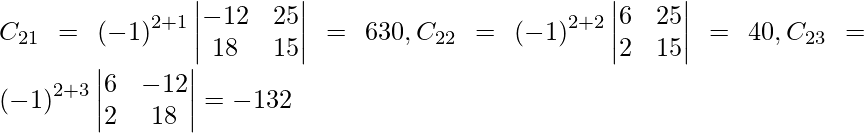
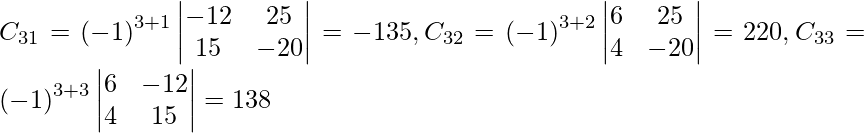
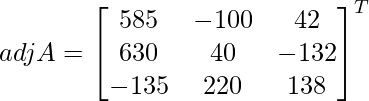
= 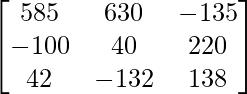
![]()
= 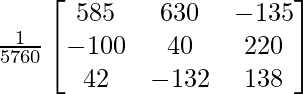
Now, X = A-1 B
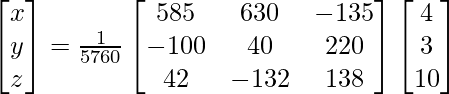
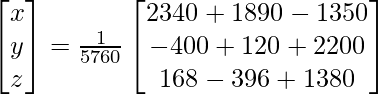
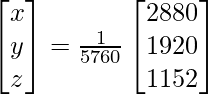
=> x = 2880/5760, y = 1920/5760 and z = 1152/5760
Therefore x = 1/2, y = 1/3 and z = 1/5.
(iv) 3x + 4y + 7z = 14
2x - y + 3z = 4
x + 2y - 3z = 0
解决方案:
A = 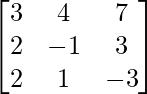
|A| = 
= 3 (3 – 3) – 4 (- 6 – 6) + 7 (2 + 2)
= 0 + 48 + 28
= 76
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
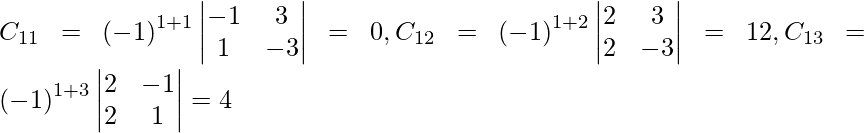
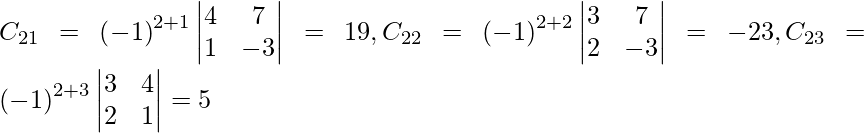
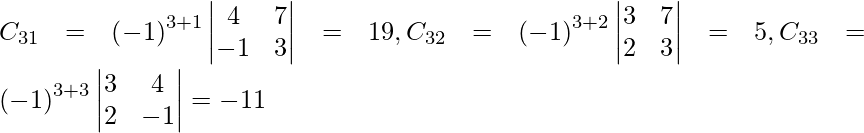
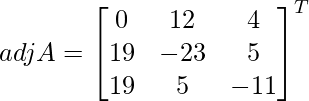
= 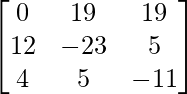
![]()
= 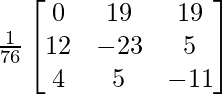
Now, X = A-1 B
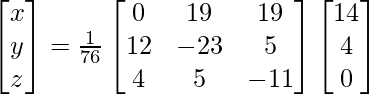
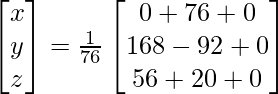
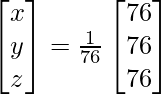
=> x = 76/76, y = 76/76 and z = 76/76
Therefore x = 1, y = 1 and z = 1.
(五) 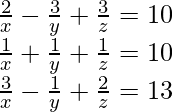
解决方案:
Let 1/x be a, 1/y be b and 1/z be c.
Here,
A = 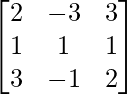
|A| = 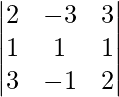
= 2 (2 + 1) + 3 (2 – 3) + 3 (-1 – 3)
= 6 – 3 – 12
= -9
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
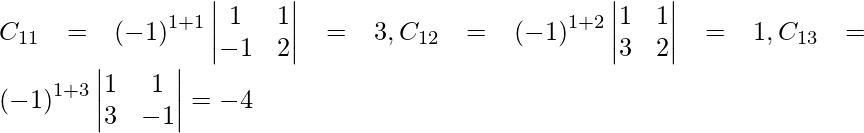
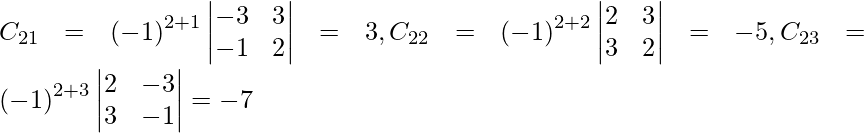
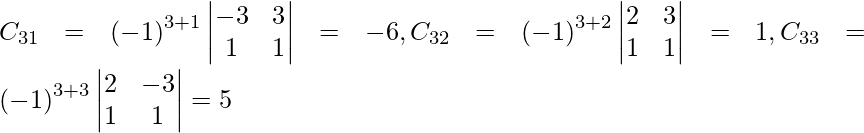
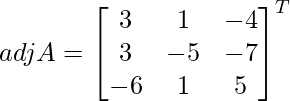
= 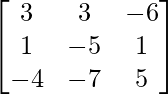
![]()
= 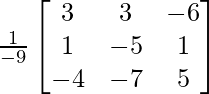
X = A-1 B
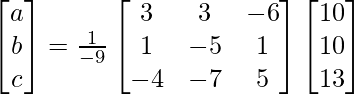
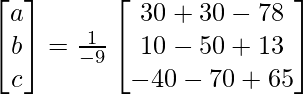
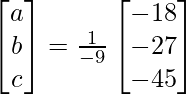
=> x = 1/a = – 9/-18, y = 1/b = – 9/- 27 and z = 1/c = -9/-45
Therefore x = 1/2, y = 1/3 and z = 1/5.
(vi) 5x + 3y + z = 16
2x + y + 3z = 19
x + 2y + 4z = 25
解决方案:
A = 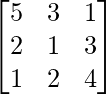
|A| = 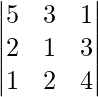
= 5 (4 – 6) – 3 (8 – 3) + 1 (4 – 1)
= -10 – 15 + 3
= – 22
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
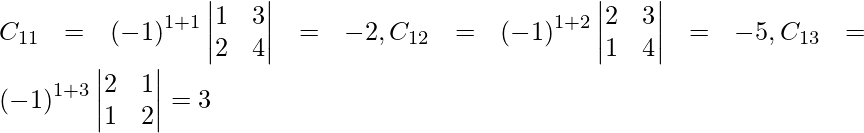

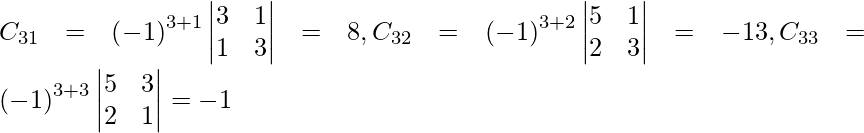
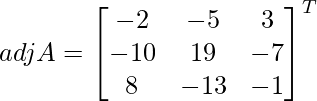
= 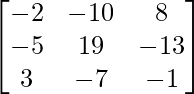
![]()
= 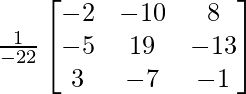
X = A-1 B
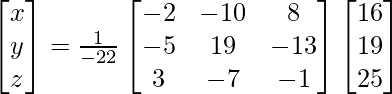
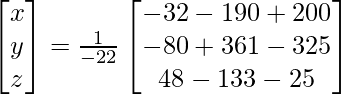
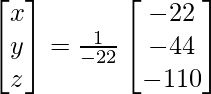
=> x = – 22/- 22, y = – 44/- 22 and z = -110/-22
Therefore x = 1, y = 2 and z = 5.
(vii) 3x + 4y + 2z = 8
2y - 3z = 3
x - 2y + 6z = -2
解决方案:
A = 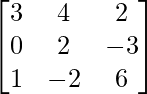
|A| = 
= 3 (12 – 6) – 4 (0 + 3) + 2 (0 – 2)
= 18 – 12 – 4
= 2
Let Cij be the cofactors of the elements aij in A.
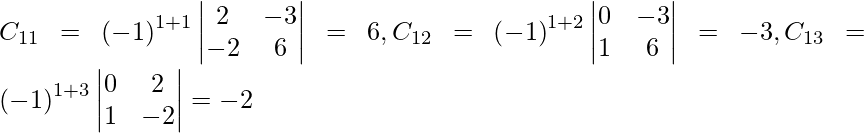
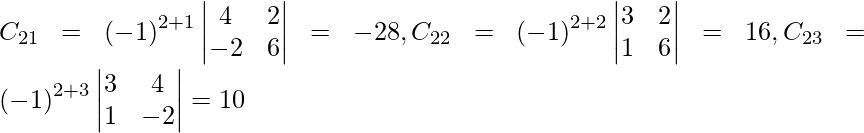
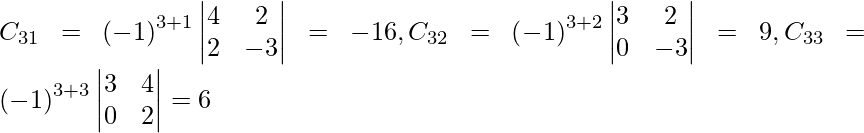
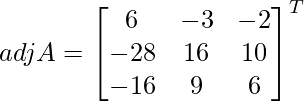
= 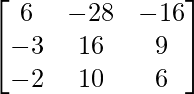
![]()
= 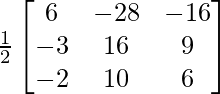
Now X = A-1 B
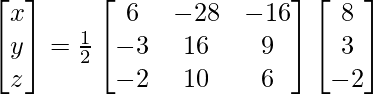
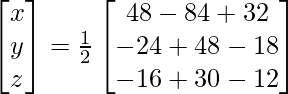

=> x = -4/2, y = 6/2 and z = 2/2
Therefore x = -2, y = 3 and z = 1.
(viii) 2x + y + z = 2
x + 3y - z = 5
3x + y - 2z = 6
解决方案:
Here,
A = 
|A| = 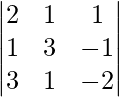
= – 10 – 1 – 8
= -19
Let Cij be the cofactors of the elements aij in A.
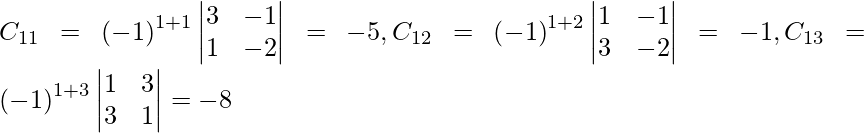
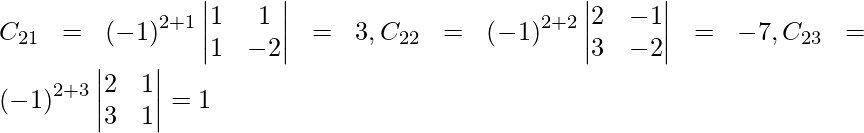

adj A = 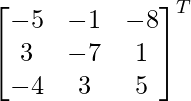
= 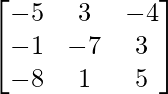
![]()
= 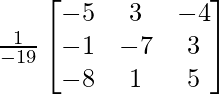
X = A-1 B
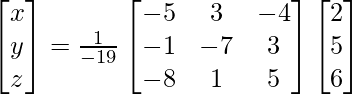
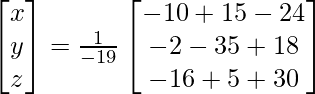
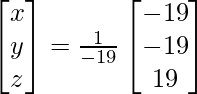
x = -19/-19, y = -19/-19 and z = 19/-19
Therefore x = 1, y = 1 and z = – 1.
(ix) 2x + 6y = 2
3x - z = -8
2x - y + z = -3
解决方案:
A = 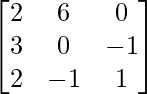
|A| = 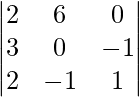
= 2 (0 – 1) – 6 (3 + 2) + 0 (-3 + 0)
= -2 – 30
= – 32
Let Cij be the cofactors of the elements aij in A.
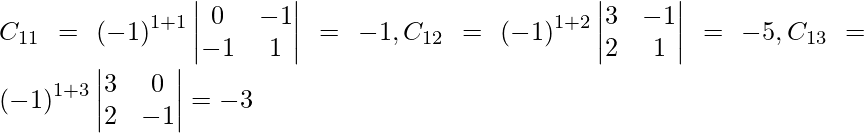
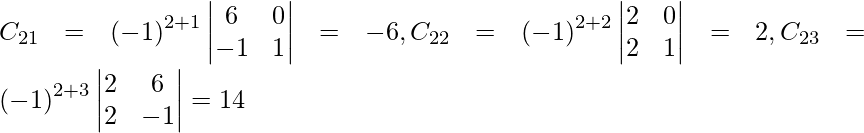
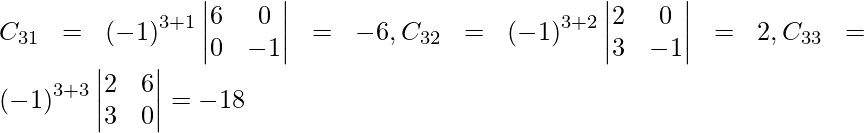
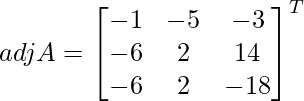
= 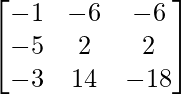
![]()
= 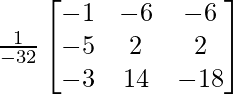
X = A-1 B
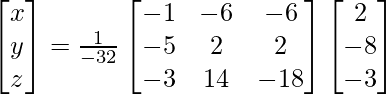
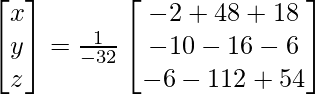
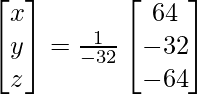
=> x = 64/-32, y = -32/-32 and z = -64/-32
Therefore x = – 2, y = 1 and z = 2.
(x) x - y + z = 2
2x - y = 0
2y - z = 1
解决方案:
A = 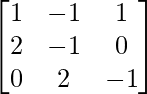
|A| = 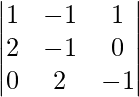
= 1 (1 – 0) + 1 (-2 – 0) + 1(4 – 0)
= 1 – 2 + 4
= 3
Let Cij be the cofactors of the elements aij in A.
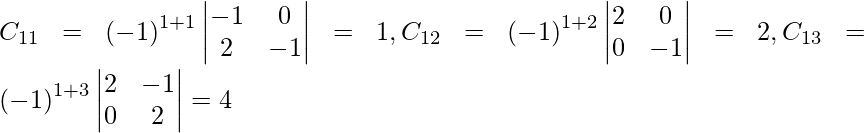
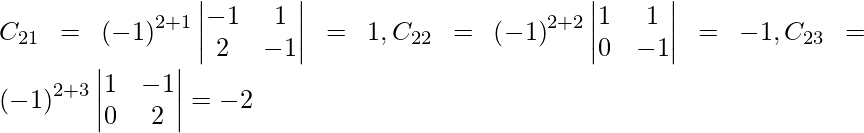
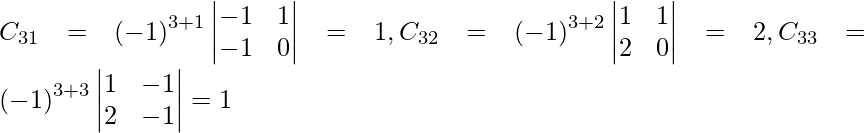
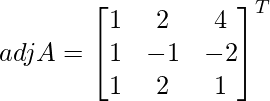
= 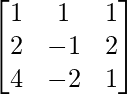
![]()
= 
X = A-1 B
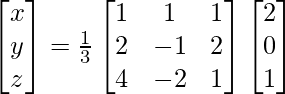
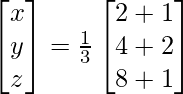
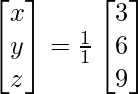
=> x = 3/3, y = 6/3 and z = 9/3
Therefore x = 1, y = 2 and z = 3.
(xi) 8x + 4y + 3z = 18
2x + y +z = 5
x + 2y + z = 5
解决方案:
A = 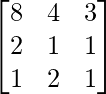
|A| = 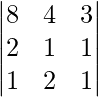
= 8 (1 – 2) – 4 (2 – 1) + 3(4 – 1)
= – 8 – 4 + 9
= -3
Let Cij be the cofactors of the elements aij in A.
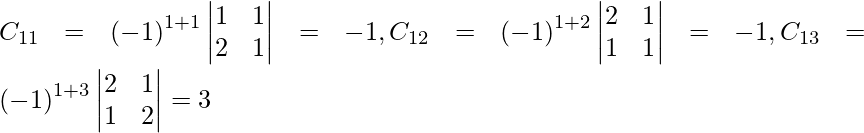
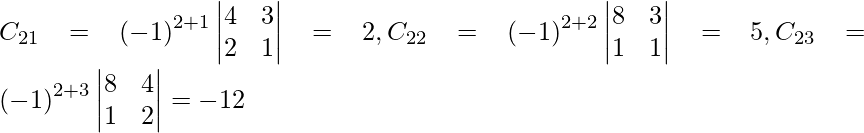
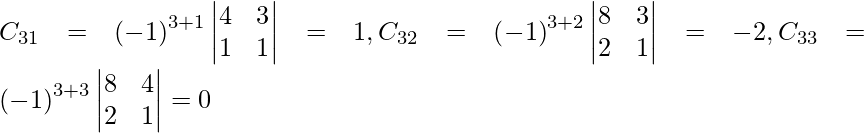
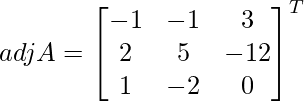
= 
![]()
= 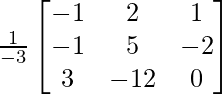
X = A-1 B
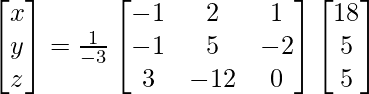
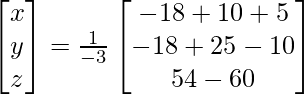
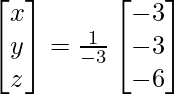
=> x = -3/-3, y = -3/-3 and z = -6/-3
Therefore x = 1, y = 1 and z = 2.
(xii) x + y + z = 6
x + 2z = 7
3x + y + z = 12
解决方案:
A = 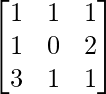
|A| = 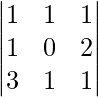
= 1 (0 – 2) – 1 (1 – 6) + 1(1 – 0)
= – 2 + 5 + 1
= 4
Let Cij be the cofactors of the elements aij in A.
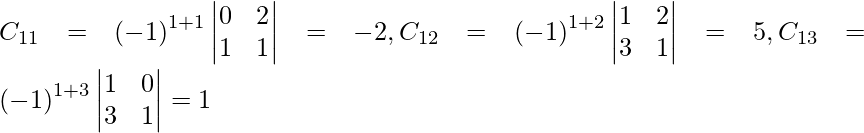

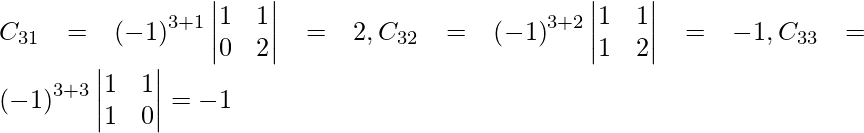
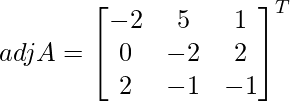
= 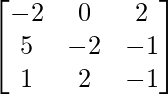
![]()
= 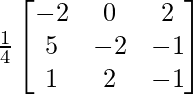
X = A-1 B
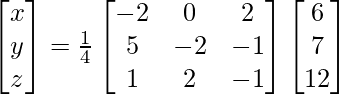
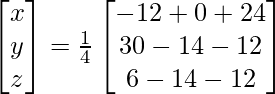
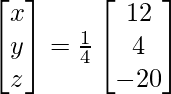
=> x = 12/4, y = 4/4 and z = -20/4
Therefore x = 3, y = 1 and z = – 5.
(十三) 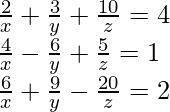 , x, y, z ≠ 0
, x, y, z ≠ 0
解决方案:
Let 1/x be a, 1/y be b and 1/z be c.
Here,
A = 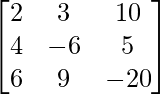
|A| = 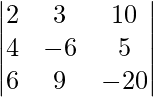
= 2 (120 – 45) – 3 (-80 – 30) + 10 (36 + 36)
= 150 + 330 + 720
= 1200
Let Cij be the cofactors of the elements aij in A.
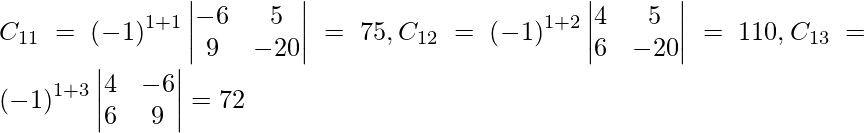
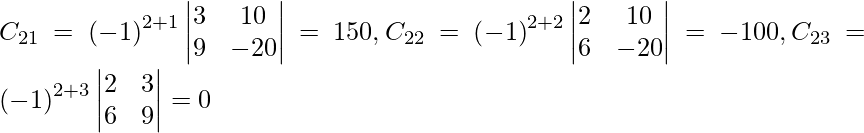
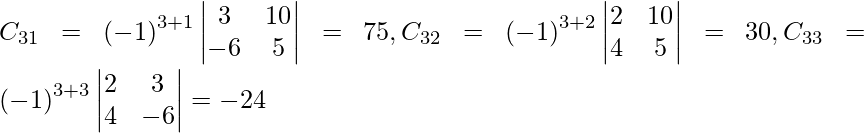
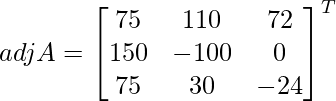
= 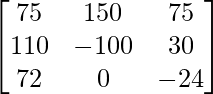
![]()
= 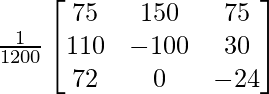
X = A-1 B
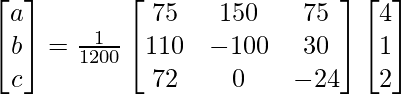
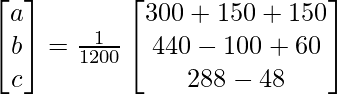
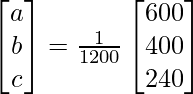
=> x = 1/a = 1200/600, y = 1/b = 1200/400 and z = 1/c = 1200/240
Therefore x = 2, y = 3 and z = 5.
(xiv) x - y + 2z = 7
3x + 4y - 5z = -5
2x - y + 3z = 12
解决方案:
A = 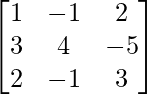
|A| = 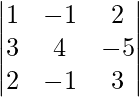
= 1 (12 – 5) + 1 (9 + 10) + 2 (-3 – 8)
= 7 + 19 – 22
= 4
Let Cij be the cofactors of the elements aij in A.
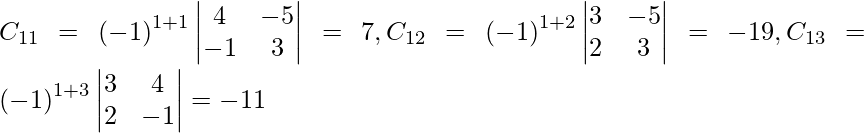
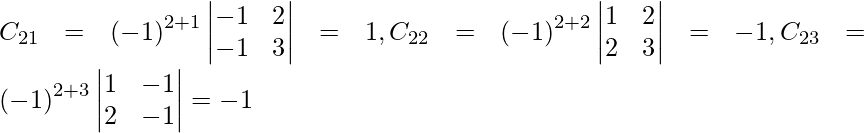
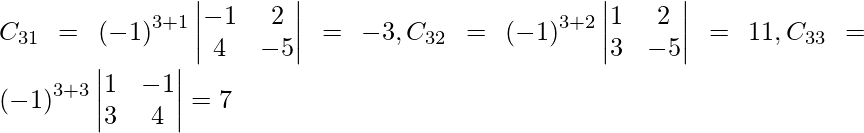
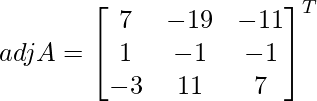
= 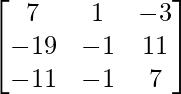
![]()
= 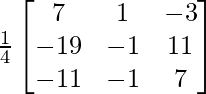
X = A-1 B
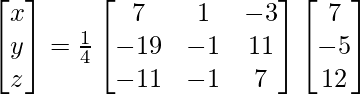
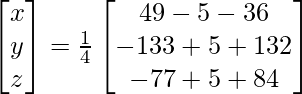
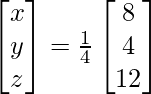
=> x = 8/4, y = 4/4 and z = 12/4
Therefore x = 2, y = 1 and z = 3.
问题 3. 证明下列线性方程组是一致的:
(i) 6x + 4y = 2
9x + 6y = 3
解决方案:
Here,
6x + 4y = 2
9x + 6y = 3
We know, AX = B
A = 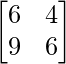 , X =
, X = ![]() and B =
and B = ![]()
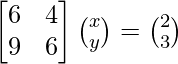
|A| = 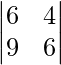
= 36 – 36
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = 6, C12 = -9, C21 = -4 and C22 = 6
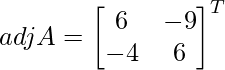
= 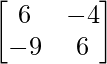
(adj A) B = 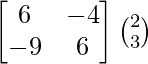
= ![]()
= ![]()
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
(ii) 2x + 3y = 5
6x + 9y = 15
解决方案:
Here,
2x + 3y = 5
6x + 9y = 15
We know, AX = B
A = 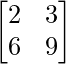 , X =
, X = ![]() and B =
and B = ![]()
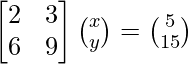
|A| = 
= 18 – 18
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = 9, C12 = -6, C21 = -3 and C22 = 2
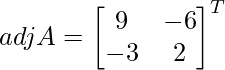
= 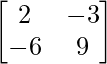
(adj A) B = 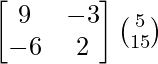
= ![]()
= ![]()
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
(iii) 5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
解决方案:
Here,
5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
We know, AX = B
A = 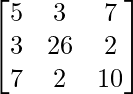 , X =
, X = ![]() and B =
and B = ![]()
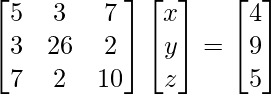
|A| = 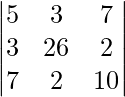
= 1280 – 48 – 1232\]
= 0
Let Cij be the cofactors of the elements aij in A.
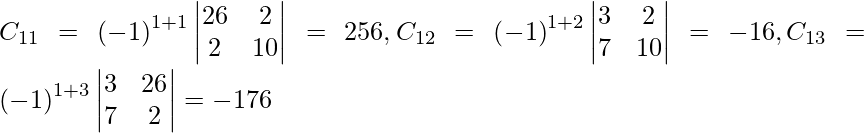
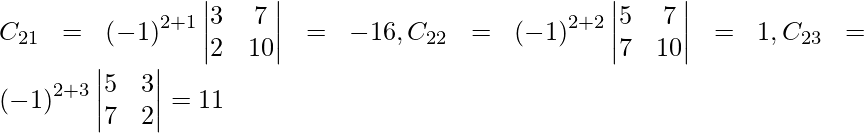
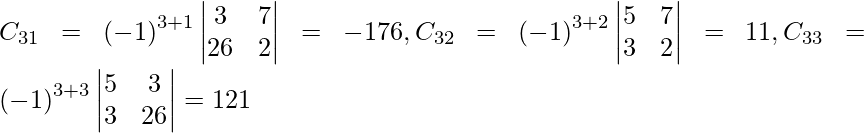
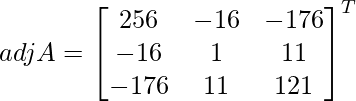
= 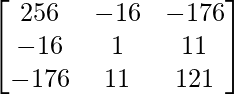
(adj A)B = 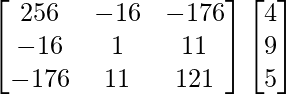
= 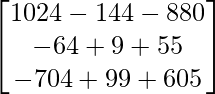
= ![]()
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
(iv) x - y + z = 3
2x + y - z = 2
-x -2y + 2z = 1
解决方案:
Here,
x − y + z = 3
2x + y − z = 2
−x −2y + 2z = 1
We know, AX = B
A = 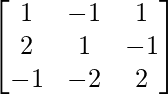 , X =
, X = ![]() and B =
and B = ![]()
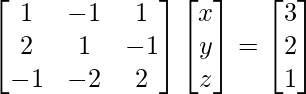
|A| = 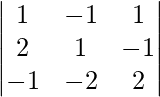
= 1\left( 2 – 2 \right) + 1\left( 4 – 1 \right) + 1( – 4 + 1)\]
= 0 + 3 – 3
= 0
Let Cij be the cofactors of the elements aij in A.
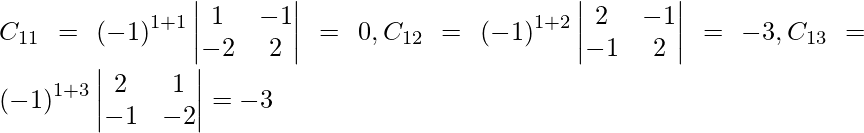
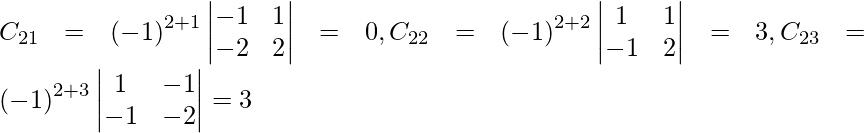
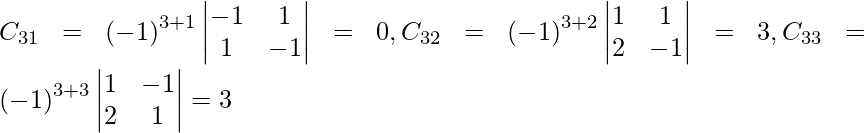

= 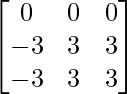
(adj A) B = 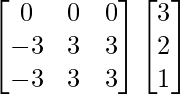
= 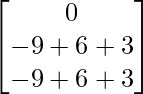
= ![]()
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
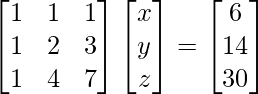
(v) x + y + z = 6
x + 2y + 3z = 14
x + 4y + 7z = 30
解决方案:
Here,
x + y + z = 6
x + 2y + 3z = 14
x + 4y + 7z = 30
A = 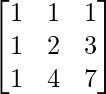 , X =
, X = ![]() and B =
and B = ![]()
|A| = 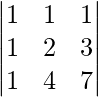
= 2 – 4 + 2
= 0
Let Cij be the cofactors of the elements aij in A.
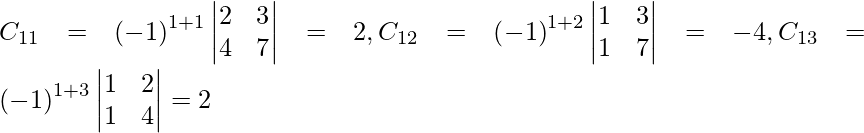
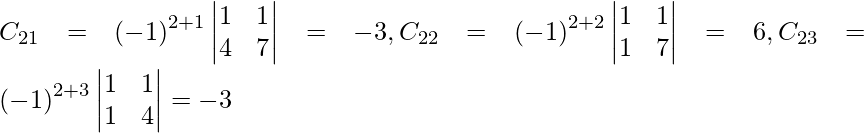
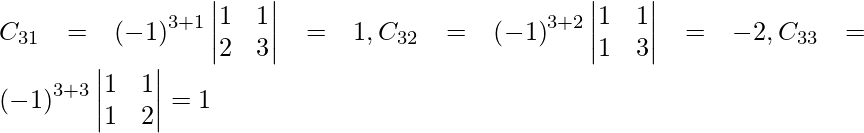
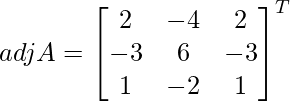
= 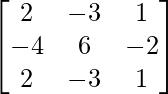
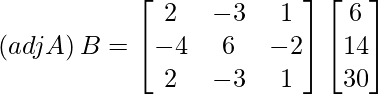
= 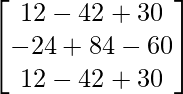
= ![]()
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
(vi) 2x + 2y - 2z = 1
4x + 4y - z = 2
6x + 6y + 2z = 3
解决方案:
Here,
2x + 2y − 2z = 1
4x + 4y − z = 2
6x + 6y + 2z = 3
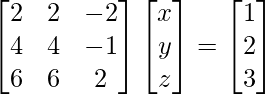
A = 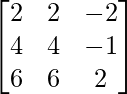 , X =
, X = ![]() and B =
and B = ![]()
|A| = 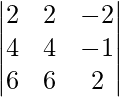
= 2 (8 + 6) – 2 (8 + 6) – 2 (24 – 24)
= 28 – 28 – 0
= 0
Let Cij be the cofactors of the elements aij in A.
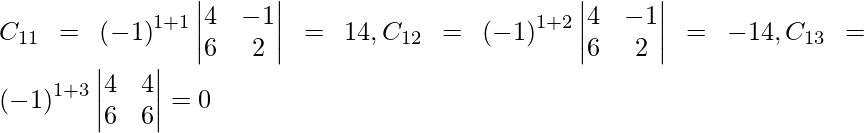
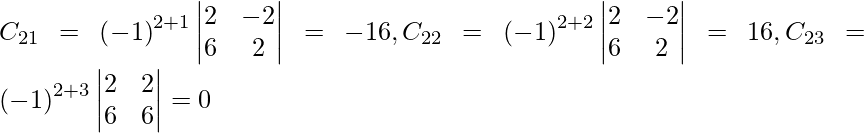
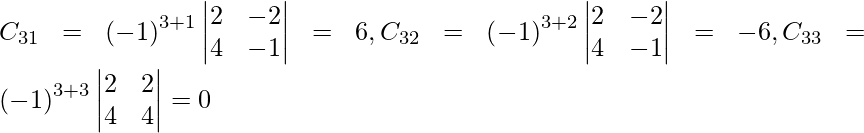
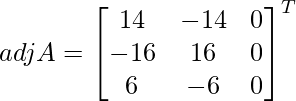
= 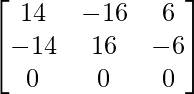
(adj A) B = 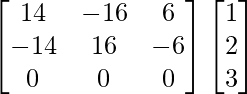
= 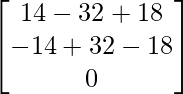
= ![]()
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
问题 4. 证明下列每一个线性方程组是不一致的:
(i) 2x + 5y = 7
6x + 15y = 13
解决方案:
The given system of equations can be expressed as follows:
AX = B
Here,
A = 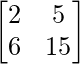 , X =
, X = ![]() and B =
and B = ![]()
Now,
|A| = 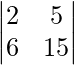
= 30 – 30
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = 15, C12 = -6, C21 = -5 and C22 = 2
adj A = 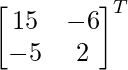
= 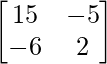
(adj A) B = 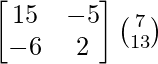
= ![]()
= ![]() ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(ii) 2x + 3y = 5
6x + 9y = 10
解决方案:
The given system of equations can be expressed as follows:
AX = B
Here,
A = 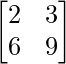 , X =
, X = ![]() and B =
and B = ![]()
|A| = 
= 18 – 18
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = 9, C12 = -6, C21 = -3 and C22 = 2
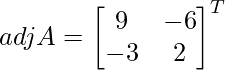
= 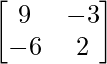
(adj A) B = 
= ![]()
= ![]() ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(iii) 4x - 2y = 3
6x - 3y = 5
解决方案:
The given system of equations can be expressed as,
AX = B
Here,
A = 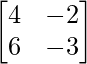 , X =
, X = ![]() and B =
and B = ![]()
|A| = 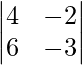
= 12 – 12
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = -3, C12 = -6, C21 = 2 and C22 = 4
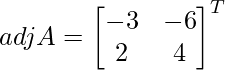
= 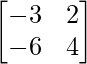
(adj A) B = 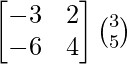
= ![]()
= ![]() ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(iv) 4x - 5y - 2z = 2
5x - 4y + 2z = -2
2x + 2y + 8z = -1
解决方案:
The given system of equations can be written as,
AX = B
Here,
A =  , X =
, X = ![]() and B =
and B = 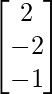
|A| = 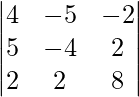
= -144 + 180 – 36
= 0
Let Cij be the cofactors of the elements aij in A.
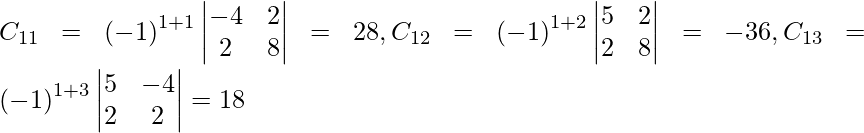
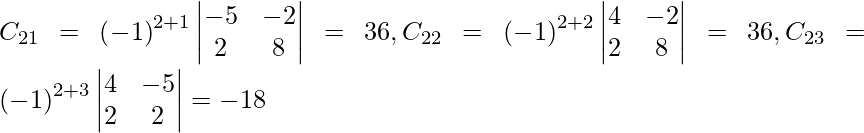
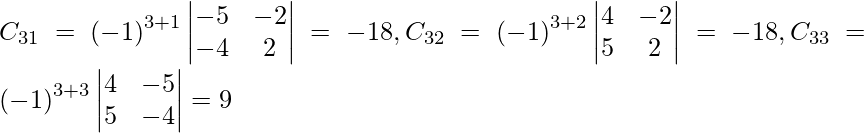
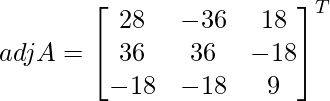
= 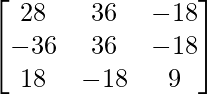
(adj A) B = 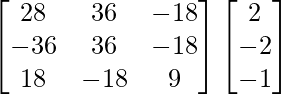
= 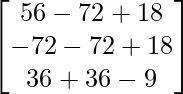
= 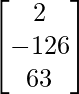 ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(v) 3x - y - 2z = 2
2y - z = -1
3x - 5y = 3
解决方案:
The given system of equations can be written as,
AX = B
Here,
A = 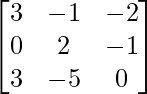 , X =
, X = ![]() and B =
and B = 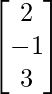
|A| = 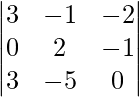
= -15 + 3 + 12
= 0
Let Cij be the cofactors of the elements aij in A.
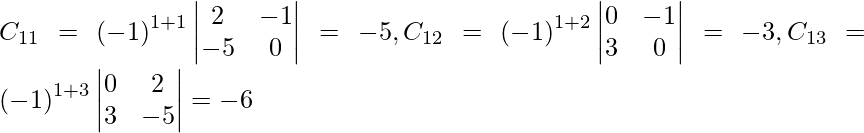
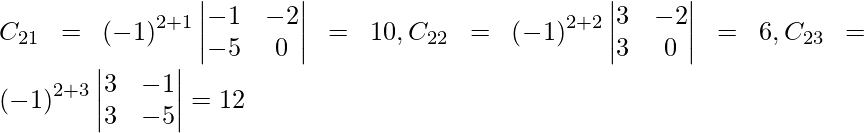
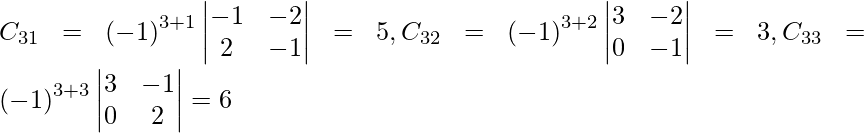
adj A = 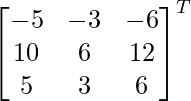
= 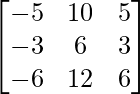
(adj A) B = 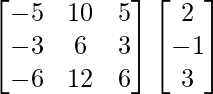
= 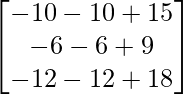
= 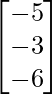 ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(vi) x + y - 2z = 5
x - 2y + z = -2
−2x + y + z = 4
解决方案:
The given system of equations can be written as,
AX = B
Here,
A = 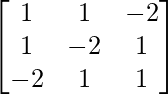 , X =
, X = ![]() and B =
and B = 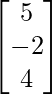
|A| = 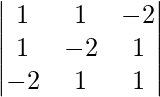
= – 3 – 3 + 6
= 0
Let Cij be the cofactors of the elements aij in A.
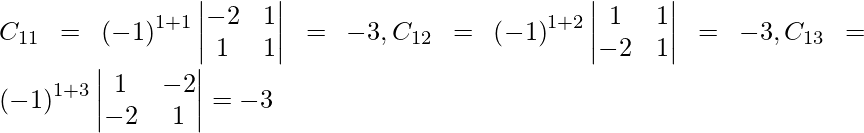
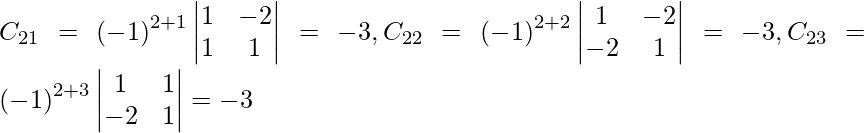
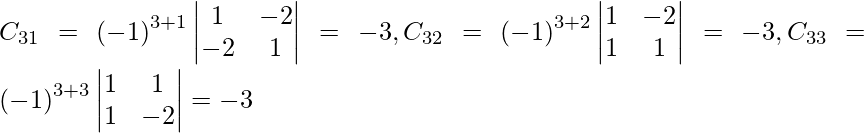
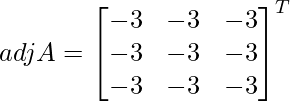
= 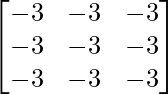
(adj A) B = 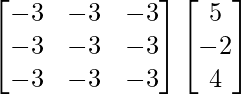
= 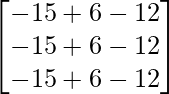
=  ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
问题 5. 如果 A = 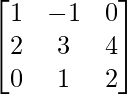 和 B =
和 B = 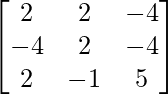 是两个方阵,求 AB 并求解线性方程组:x - y = 3, 2x + 3y + 4z = 17, y + 2z = 7。
是两个方阵,求 AB 并求解线性方程组:x - y = 3, 2x + 3y + 4z = 17, y + 2z = 7。
解决方案:
Here,
A = 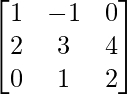 and B =
and B = 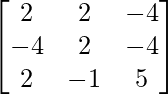
Now,
AB = 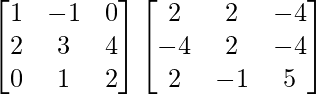
AB = 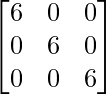
AB = 
AB = 6I
![]() = I
= I
![]()
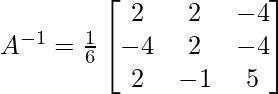
X = A-1 B
X = 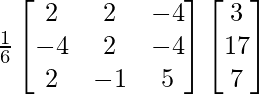
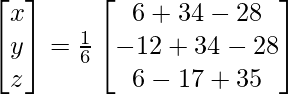
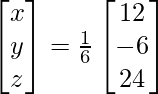
Therefore x = 2, y = -1 and z = 4.
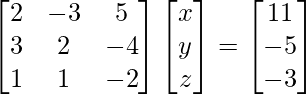
问题 6. 如果 A = 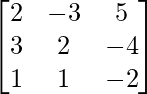 ,找到 A -1并因此求解线性方程组 2x - 3y + 5z = 11, 3x + 2y - 4z = -5, x + y + 2z = -3。
,找到 A -1并因此求解线性方程组 2x - 3y + 5z = 11, 3x + 2y - 4z = -5, x + y + 2z = -3。
解决方案:
Here,
A = 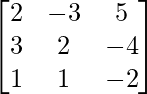
|A| = 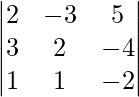
= 0 – 6 + 5
= -1
Let Cij be the cofactors of the elements aij in A.
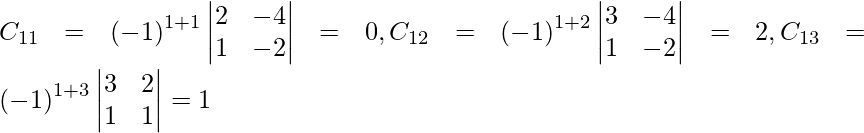
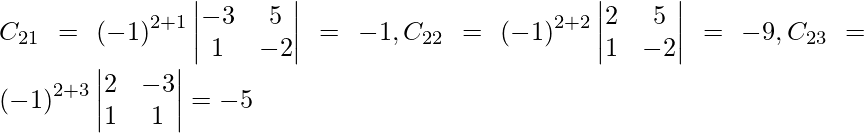
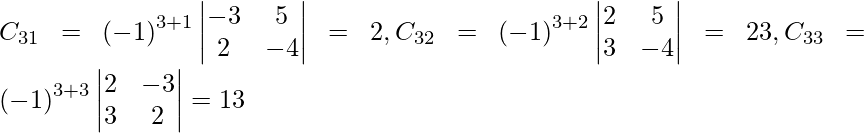
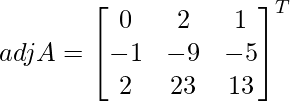
= 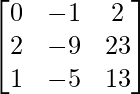
![]()
= 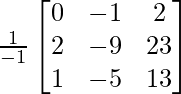
X = A-1 B



=> x = – 1/- 1, y = -2/-1\ and z = -3/-1
Therefore x = 1, y = 2 and z = 3.
问题 7. 求 A −1 ,如果 A = 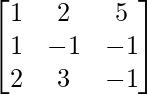 .因此求解以下线性方程组:x + 2y + 5z = 10, x - y - z = -2, 2x + 3y - z = -11。
.因此求解以下线性方程组:x + 2y + 5z = 10, x - y - z = -2, 2x + 3y - z = -11。
解决方案:
A = 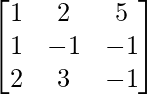
|A| = 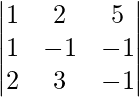
= 4 – 2 + 25
= 27
Let Cij be the cofactors of the elements aij in A.
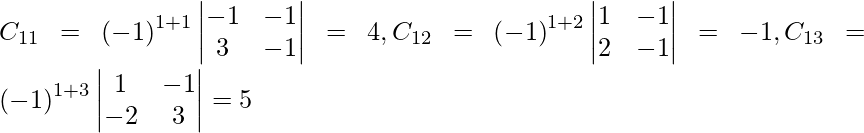
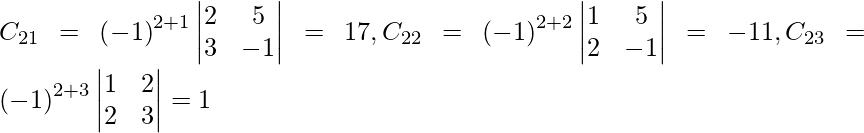
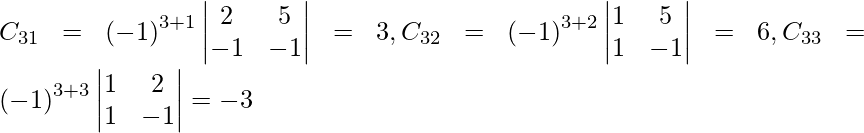
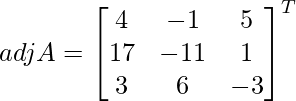
= 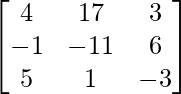
![]()
= 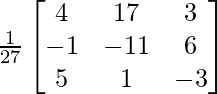
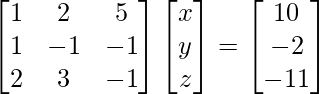
X = A-1 B
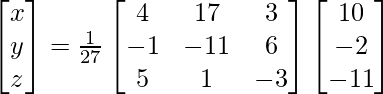
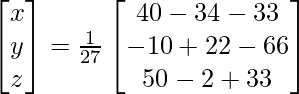
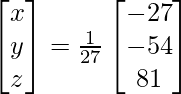
=> x = -27/27, y = -54/27 and z = 81/27
Therefore, x = – 1, y = -2 and z = 3.