第 11 类 RD Sharma 解决方案 - 第 18 章二项式定理 - 练习 18.2 |设置 3

问题 27. 如果 (x + α) ⁿ的展开式中的^第3项、第 4 项、第 5 项和^第6 项分别为^a 、b、c和 d，证明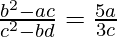$\frac{b^2-ac}{c^2-bd}=\frac{5a}{3c}$ .

解决方案：

We are given, (x + α)ⁿ

So, T₃ = a = ⁿC₂ x^n-2 α²

T₄ = b = ⁿC₃ x^n-3 α³

T₅ = c = ⁿC₄ x^n-4 α⁴

T₆ = d = ⁿC₅ x^n-5 α⁵

We need to prove that, $\frac{b^2-ac}{c^2-bd}=\frac{5a}{3c}$

=> $\frac{b^2-ac}{a}=\frac{5(c^2-bd)}{3c}$

=> $\frac{b^2-ac}{ab}=\frac{5(c^2-bd)}{3bc}$

=> $\frac{b}{a}-\frac{c}{b}=\frac{5}{3}\left[\frac{c}{b}-\frac{d}{c}\right]$   

=> $\frac{^nC_3x^{n-3}α^3}{^nC_2x^{n-2}α^2}-\frac{^nC_4x^{n-4}α^4}{^nC_3x^{n-3}α^3}=\frac{5}{3}\left[\frac{^nC_4x^{n-4}α^4}{^nC_3x^{n-3}α^3}-\frac{^nC_5x^{n-5}α^5}{^nC_4x^{n-4}α^4}\right]$

=> $\left[\frac{^nC_3}{^nC_2}-\frac{^nC_4}{^nC_3}\right]\frac{\alpha}{x}=\frac{5\alpha}{3x}\left[\frac{^nC_4}{^nC_3}-\frac{^nC_5}{^nC_4}\right]$

=> $\left[\frac{n-2}{3}-\frac{n-3}{4}\right]=\frac{5}{3}\left[\frac{n-3}{4}-\frac{n-4}{5}\right]$

=> $\frac{4n-8-3n+9}{12}=\frac{5}{3}\left[\frac{5n-15-4n+16}{20}\right]$

=> $\frac{n+1}{12}=\frac{5}{3}\left[\frac{n+1}{20}\right]$

=> $\frac{n+1}{12}=\frac{n+1}{12}$

Hence proved.

问题 28. 如果 (x + α) ⁿ的展开式中的^第6 项、第 7 项、^第8 项和^第9 项分别为^a 、b、c和 d，证明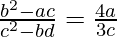： $\frac{b^2-ac}{c^2-bd}=\frac{4a}{3c}$ .

解决方案：

We are given, (x + α)ⁿ

So, T₆ = a = ⁿC₅ x^n-5 α⁵

T₇ = b = ⁿC₆ x^n-6 α⁶

T₈ = c = ⁿC₇ x^n-7 α⁷

T₉ = d = ⁿC₈ x^n-8 α⁸

We need to prove that, $\frac{b^2-ac}{c^2-bd}=\frac{4a}{3c}$

=> $\frac{b^2-ac}{a}=\frac{4(c^2-bd)}{3c}$

=> $\frac{b^2-ac}{ab}=\frac{4(c^2-bd)}{3bc}$

=> $\frac{b}{a}-\frac{c}{b}=\frac{4}{3}\left[\frac{c}{b}-\frac{d}{c}\right]$

=> $\frac{^nC_6x^{n-6}α^6}{^nC_5x^{n-5}α^5}-\frac{^nC_7x^{n-7}α^7}{^nC_6x^{n-6}α^6}=\frac{4}{3}\left[\frac{^nC_7x^{n-7}α^7}{^nC_6x^{n-6}α^6}-\frac{^nC_8x^{n-8}α^8}{^nC_7x^{n-7}α^7}\right]$

=> $\left[\frac{^nC_6}{^nC_5}-\frac{^nC_7}{^nC_6}\right]\frac{\alpha}{x}=\frac{4\alpha}{3x}\left[\frac{^nC_7}{^nC_6}-\frac{^nC_8}{^nC_7}\right]$

=> $\left[\frac{n-5}{6}-\frac{n-6}{7}\right]=\frac{4}{3}\left[\frac{n-6}{7}-\frac{n-7}{8}\right]$

=> $\frac{7n-35-6n+36}{42}=\frac{4}{3}\left[\frac{8n-48-7n+49}{56}\right]$

=> $\frac{n+1}{42}=\frac{4}{3}\left[\frac{n+1}{56}\right]$

=> $\frac{n+1}{42}=\frac{n+1}{42}$

Hence proved.

问题 29. 如果 (1+x) ⁿ的展开式中的三个连续项的系数分别为 76、95和 76，求 n。

解决方案：

We are given, (1+x)ⁿ

Let the three consecutive terms be r^th, (r+1)^th and (r+2)^th.

We know the coefficient of r^th term of a binomial expression is given by ⁿC_r-1.

Coefficient of r^th term = ⁿC_r-1 = 76

Coefficient of (r+1)^th term = ⁿC_r+1-1 = ⁿC_r = 95

Coefficient of (r+2)^th term = ⁿC_r+2-1 = ⁿC_r+1 = 76

Now, $\frac{^nC_{r+1}}{^nC_r}=\frac{76}{95}$

=> $\frac{n-(r+1)+1}{r+1}=\frac{76}{95}$

=> $\frac{n-r}{r+1}=\frac{4}{5}$

=> 5n − 5r = 4r + 4

=> 5n − 9r = 4  . . . . (1)

Also, $\frac{^nC_{r}}{^nC_{r-1}}=\frac{95}{76}$

=> $\frac{n-r+1}{r}=\frac{5}{4}$

=> 4n − 4r + 4 = 5r

=> 4n − r = −4  . . . . (2)

Subtracting (2) from (1), we get,

=> n = 4 + 4

=> n = 8

Therefore, the value of n is 8.

问题 30. 如果(x + a) ⁿ的展开式中^的第 6^次、第 7^次和第 8 次分别为 112、7和 1/4，求 x、a和 n。

解决方案：

We are given, (x + a)ⁿ

Also, T₆ = ⁿC₅ x^n-5 a⁵ = 112

T₇ = ⁿC₆ x^n-6 a⁶ = 7

T₈ = ⁿC₇ x^n-7 a⁷ = 1/4

Now, $\frac{^nC_6x^{n-6}a^6}{^nC_5x^{n-5}a^5}=\frac{7}{112}$

=> $\frac{^nC_{n-6}x^{n-6}a^6}{^nC_{n-5}x^{n-5}a^5}=\frac{7}{112}$

=> $\frac{^nC_{n-6}}{^nC_{n-5}}×\frac{a}{x}=\frac{1}{16}$

=> $\frac{n-6+1}{n-(n-5)+1}×\frac{a}{x}=\frac{1}{16}$

=> $\frac{n-5}{6}×\frac{a}{x}=\frac{1}{16}$

=> $\frac{a}{x}=\frac{3}{8(n-5)}$   . . . . (1)

Also, $\frac{^nC_7x^{n-7}a^7}{^nC_6x^{n-6}a^6}=\frac{\frac{1}{4}}{7}$

=> $\frac{^nC_{n-7}x^{n-7}a^7}{^nC_{n-6}x^{n-6}a^6}=\frac{1}{28}$

=> $\frac{^nC_{n-7}}{^nC_{n-6}}×\frac{a}{x}=\frac{1}{28}$

=> $\frac{n-7+1}{n-(n-6)+1}×\frac{a}{x}=\frac{1}{28}$

=> $\frac{n-6}{7}×\frac{a}{x}=\frac{1}{28}$

=> $\frac{a}{x}=\frac{1}{4(n-6)}$   . . . . (2)

From (1) and (2), we get,

=> $\frac{3}{8(n-5)} = \frac{1}{4(n-6)}$

=> $\frac{3}{2(n-5)} = \frac{1}{n-6}$

=> 3n − 18 = 2n − 10

=> n = 8

Putting n = 8 in (2), we get,

=> $\frac{a}{x}=\frac{1}{4(8-6)}$

=> $\frac{a}{x}=\frac{1}{8}$

=> x = 8a

Now, ⁿC₅ x^n-5 a⁵ = 112

=> ⁸C₅ x^8-5 a⁵ = 112

=> ⁸C₅ (8a)³ a⁵ = 112

=> $\frac{8×7×6}{3×2}×512×a^3×a^5 = 112$

=> a⁸ = $\frac{1}{256}$

=> a⁸ = $(\frac{1}{2})^8$

=> a = 1/2

So, x = 8 (1/2) = 4

Therefore, the value of x, a and n is 4, 1/2 and 8 respectively.

问题 31. 如果第 2^次，第 3^次， (x + a) ⁿ的展开式中的第 4 和第 4 分别^为240、720和 1080，求 x、a和 n。

解决方案：

We are given, (x + a)ⁿ

Also, T₂ = ⁿC₁ x^n-1 a = 240

T₃ = ⁿC₂ x^n-2 a² = 720

T₄ = ⁿC₃ x^n-3 a³ = 1080

Now, $\frac{^nC_3x^{n-3}a^3}{^nC_2x^{n-2}a^2}=\frac{1080}{720}$

=> $\frac{^nC_3}{^nC_2}×\frac{a}{x}=\frac{3}{2}$

=> $\frac{n-3+1}{2+1}×\frac{a}{x}=\frac{3}{2}$

=> $\frac{n-2}{3}×\frac{a}{x}=\frac{3}{2}$

=> $\frac{a}{x}=\frac{9}{2(n-2)}$  . . . . (1)

Also, $\frac{^nC_2x^{n-2}a^2}{^nC_1x^{n-1}a}=\frac{720}{240}$

=> $\frac{^nC_2}{^nC_1}×\frac{a}{x}=3$

=> $\frac{n-2+1}{2}×\frac{a}{x}=3$

=> $\frac{n-1}{2}×\frac{a}{x}=3$

=> $\frac{a}{x}=\frac{6}{n-1}$   . . . . (2)

From (1) and (2), we get,

=> $\frac{9}{2(n-2)}=\frac{6}{n-1}$

=> 12n − 24 = 9n − 9

=> 3n = 15

=> n = 5

Putting n = 5 in (2), we get,

=> $\frac{a}{x}=\frac{6}{5-1}$

=> $\frac{a}{x}=\frac{6}{4}$

=> $\frac{a}{x}=\frac{3}{2}$

=> $a = \frac{3}{2}x$

Now, ⁿC₁ x^n-1 a = 240

=> ⁵C₁ x^5-1 (3x/2) = 240

=> ⁵C₁ x⁵ (3/2) = 240

=> $\frac{5×4!}{4!}×x^5×\frac{3}{2} = 240$

=> $x^5=\frac{240×2}{5×3}$

=> x⁵ = 32

=> x⁵ = 2⁵

=> x = 2

So, a = (3/2) (2) = 3

Therefore, the value of x, a and n is 2, 3 and 5 respectively.

问题 32.如果前三个项分别是729、7290 和 30375 ，则在 (a+b) ⁿ的展开式中找到 a、b 和 n 。

解决方案：

We are given, (a+b)ⁿ

Also, T₁ = ⁿC₀ aⁿ = 729

T₂ = ⁿC₁ a^n-1 b¹ = 7290

T₃ = ⁿC₂ a^n-2 b² = 30375

Now, $\frac{^nC_1a^{n-1}b^1}{^nC_0a^n} = \frac{7290}{729}$

=> $^nC_{n-1}×\frac{b}{a} = 10$

=> $\frac{b}{a} = \frac{10}{n}$    . . . . (1)

Also, $\frac{^nC_2a^{n-2}b^2}{^nC_1a^{n-1}b} = \frac{30375}{7290}$

=> $\frac{^nC_{n-2}}{^nC_{n-1}}×\frac{b}{a} = \frac{25}{6}$

=> $\frac{n-2+1}{n-(n-1)+1}×\frac{b}{a} = \frac{25}{6}$

=> $\frac{n-1}{2}×\frac{b}{a} = \frac{25}{6}$

=> $\frac{b}{a} = \frac{25}{3(n-1)}$  . . . . (2)

From (1) and (2), we get,

=> $\frac{10}{n} = \frac{25}{3(n-1)}$

=> 30n − 30 = 25n 

=> 5n = 30

=> n = 6

So, ⁿC₀ aⁿ = 729

=> a⁶ = 3⁶

=> a = 3

Putting a = 3 in (2), we get,

=> $\frac{b}{3} = \frac{25}{3(6-1)}$

=> $\frac{b}{3} = \frac{5}{3}$

=> b = 5

Therefore, the value of a, b and n is 3, 5 and 6 respectively.

问题 33. 如果 (3+ax) ⁹的展开式中 x ²和 x ³的系数相等，求 a。

解决方案：

We have, (3+ax)⁹ = ⁹C₀ 3⁹ + ⁹C₁ 3⁸ (ax)¹ + ⁹C₂ 3⁷ (ax)² + ⁹C₃ 3⁶ (ax)³ + . . . .  

Coefficient of x²  = ⁹C₂ 3⁷ a²

Coefficient of x³  = ⁹C₃ 3⁶ a³

According to the question, we have,

=> ⁹C₂ 3⁷ a² = ⁹C₃ 3⁶ a³

=> $\frac{9×8}{2×1}×3=\frac{9×8×7}{3×2×1}×a$

=> 81 = 63 a

=> a = 9/7

Therefore, the value of a is 9/7.

问题 34. 如果 (2+ax) ⁴的展开式中 x 和 x ³的系数相等，求 a。

解决方案：

We have, (2+ax)⁴ = ⁴C₀ 2⁴ + ⁴C₁ 2³ (ax)¹ + ⁴C₂ 2² (ax)² + ⁴C₃ 2 (ax)³ + . . . . 

Coefficient of x  = ⁴C₁ 2³ a

Coefficient of x³  = ⁴C₃ 2 a³

According to the question, we have,

=> ⁴C₁ 2³ a = ⁴C₃ 2 a³

=> ⁴C₃ 2³ a = ⁴C₃ 2 a³

=> 8a = 2a³

=> 2a (a − 4) = 0

=> a = 0 or a = 4

Therefore, the value of a is 0 or 4.

问题 35. 如果在展开式中没有 x 的项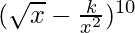$(\sqrt{x}-\frac{k}{x^2})^{10}$是405，求k的值。

解决方案：

We have, $(\sqrt{x}-\frac{k}{x^2})^{10}$

The general term of this expression will be,

T_r+1 = $^{10}C_r(\sqrt{x})^{10-r}(-\frac{k}{x^2})^{r}$

= $^{10}C_r.(x)^{\frac{10-r}{2}-2r}(-k)^r$

If the term is independent of x , we must have,

=> $\frac{10-r}{2}-2r=0$

=> 10 − r − 4r = 0

=> 5r = 10

=> r = 2

Therefore, the required term is 3^rd term.

So, we have, 

=> $^{10}C_2(\sqrt{x})^{10-2}(-\frac{k}{x^2})^{2}$ = 405

=> $^{10}C_2(\sqrt{x})^{8}(\frac{k^2}{x^4})$ = 405

=> $^{10}C_2(x^{4})(\frac{k^2}{x^4})$ = 405 

=> $\frac{10×9}{2×1}×k^2$ = 405

=> 45k² = 405

=> k² = 9

=> k = 3

Therefore, the value of k is 3.

问题 36. 求展开式 (y ^1/2 + x ^1/3 ) ⁿ中的第六项，如果倒数第三项的二项式系数为 45。

解决方案：

We have, (y + x)ⁿ

The third term of the expansion from the end is (n + 1 − 3 + 1)^th term = (n − 1)^th term. 

=> T_n-1 = T_n-2+1 = ⁿC_n-2 (y^1/2)^n-(n-2) (x^1/3)^n-2 

The coefficient of this term is given, i.e., 45.

=> ⁿC_n-2 = 45

=> n (n − 1)/2 = 45

=> n (n − 1) = 90

=> n² − n − 90 = 0

=> n² − 10n + 9n − 90 = 0

=> n(n−10) + 9 (n−10) = 0

=> n = 10 or n = −9 (ignored)

So, the sixth term of the expansion is T₆ = T₅₊₁

= ¹⁰C_10-5 (y^1/2)^10-(10-5) (x^1/3)^10-5 

= ¹⁰C₅ (y^1/2)⁵ (x^1/3)⁵

= 252 (y^5/2) (x^5/3)

问题 37. 如果 p 是实数，如果 (p/2 + 2) ⁸展开式的中项是 1120，求 p。

解决方案：

We have, (p/2 + 2)⁸

Total number of terms is 8 + 1 = 9 (odd number).

The middle term is (9+1)/2 = 5th term.

Therefore, we get T₅ = T₄₊₁ = 1120

=> ⁸C₄ (p/2)^8-4 (2)⁴ = 1120

=> 70 (p/2)⁴ (2)⁴ = 1120

=> 70p⁴ = 1120

=> p⁴ = 16

=> p⁴ = 2⁴

=> p = 2

Therefore, the value of p is 2.

问题 38. 在二项式中找到 n $(\sqrt[2]2+\frac{1}{\sqrt[3]3})^n$ , 如果第 7 项从头到尾的比例是 1/6。

解决方案：

We have, $(\sqrt[2]2+\frac{1}{\sqrt[3]3})^n$

7^th term from the beginning is $^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]3})^6$.

And 7^th term from the end is $^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]3})^{n-6}$.

According to the question, we have,

=> $\frac{^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]3})^6}{^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]3})^{n-6}}=\frac{1}{6}$

=> $(\sqrt[3]2)^{n-12}(\frac{1}{\sqrt[3]3})^{12-n}=\frac{1}{6}$

=> $(\sqrt[3]2)^{n-12}(\sqrt[3]3)^{n-12}=\frac{1}{6}$

=> $(6)^{\frac{n-12}{3}}=6^{-1}$

=> (n − 12)/3 = −1

=> n − 12 = −3

=> n = 9

Therefore, the value of n is 9.

问题 39. 如果从头到尾的第七项在二项式展开$(\sqrt[2]2+\frac{1}{\sqrt[3]2})^n$相等，求n。

解决方案：

We have, $(\sqrt[2]2+\frac{1}{\sqrt[3]2})^n$

7^th term from the beginning is $^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]2})^6$.

And 7^th term from the end is $^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]2})^{n-6}$.

According to the question, we have,

=> $^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]2})^6 = \hspace{0.1cm}^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]2})^{n-6}$

=> $(\sqrt[3]2)^{n-12}=(\sqrt[3]2)^{12-n}$

=> n − 12 = 12 − n

=> 2n = 24

=> n = 12

Therefore, the value of n is 12.