第12类RD Sharma解决方案–第18章，最大值和最小值–练习18.5 |套装3

问题31.在抛物线x ² = 2y上找到最接近点(0，5)的点。

解决方案：

The given equation of the curve is 

x² = 2y ……(i)

Let P(x, y) be a point on the given curve, and 

Q be the square of the distance between P and A(0, 5). 

Q = x² + (y – 5)²  ……..(ii)

= 2y + (y – 5)²

On differentiating w.r.t. y, we get

dQ/dy = 2 + 2(y – 5)

For maxima and minima,

Put dQ/dy = 0

⇒ 2 + 2y – 10 = 0

⇒ y = 4

Now,

When y = 4, d²Q/dy² = 2 > 0

So, y = 4 is the point of local minima

Now put the value of y in eq(1), we get

x = ±2√2

So, P(±2√2, 4) is the closest point on the curve to A(0, 5).

问题32在抛物线y = x ² + 7x + 2上找到最接近直线y = 3x – 3的点的坐标。

解决方案：

The given equation of parabola is

y = x² + 7x + 2   ……(i)

closest to the straight line y = 3x – 3         ……(ii)

Let us considered P(x, y) be the point on the given parabola which is closest to the line y = 3x – 3

Let Q be the perpendicular distance from P to the line y = 3x – 3

Q = 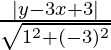$\frac{|y - 3x+3|}{\sqrt{1^2+(-3)^2}}$

= $\frac{|x² + 7x + 2-3x +3|}{√10}$

On differentiating w.r.t. x, we get

dQ/dx = (2x +4) / √10

For maxima or minima, we have

Put dQ/dx = 0

⇒ (2x + y)/√10 = 0

⇒ x = -2

Now put the value of x in eq(i), we get

 y = 4 – 14 + 2 = -8

When x = -2 and y = -8, d²Q/dx² = 2/√10 > 0

So, x = -2, and y = -8 is the point of local minima,

Hence, P(-2, -8)is the closest point on the parabola to the line y = 3x-3.

问题33在曲线y ² = 2x上找到距该点(1、4)的最小距离的点。

解决方案：

The given equation of the curve is 

y² = 2x  …..(i)

Let P(x, y) be a point on the given curve, which is minimum distance from the point A(1, 4) and 

Q square of the length of AP

Q = (x – 1)² + (y – 4)²

= x² + 1 – 2x +y2 +16 – 8y

= x² – 2x +2x+17 – 8y

= y⁴/4 – 8y +17              [Since y² = 2x]

On differentiating w.r.t. y, we get

dQ/dy = y³ – 8

For maxima and minima, we have

Put dQ/dy = 0

y³ – 8 = 0

y³ = 2³

y = 2

When y = 2, d²S/dy² = 3y² = 12 > 0

So, y = 2 is the point of local minima,

We have

x = y²/2 = 4/2 = 2

Hence, P(2, 2) is at a minimum distance from the point A(1, 4).

问题34.求出曲线的最大斜率y = -x ³ + 3x ² + 2x – 27。

解决方案：

The given equation of curve is

y = x³ + 3x² + 2x – 27          …..(i)

The slope of the given equation of the curve is 

m = dy/dx = −3x² + 6x + 2     …..(ii)

On differentiating w.r.t. x, we get

dm/dx = -6x + 6

Again differentiating w.r.t. x, we get

d²m/dx² = -6 < 0

For maxima and minima,

Put dm/dx = 0

⇒ -6x + 6 = 0

⇒ x = 1

When x = 1, d²m/dx² = -6 < 0

So, x = 1 is point of local maxima

Hence, the maximum slope of the given curve is  = -3 + 6 + 2 = 5

问题35.每天产生X无线电集合的总成本为(x ^2/4 + 35X + 25)和每组价格在它们可出售为(50 – X / 2)。查找每日产出以最大化总利润。  

解决方案：

Given, 

The cost of producing x radio sets is Rs. x²/4 + 35x + 25

And selling price of x radio is Rs. x(50 – x/2)

So, 

The profit on x radio sets is

P = 50x – x²/2 – x²/4 -35x – 25

On differentiating w.r.t. y, we get

dp/dx = 50 – x – x/2- 35

= 15 – 3x/2

For maxima and minima,

Put, dp/dx = 0

⇒ 15 – 3x/2 = 0

⇒ x = 10

When x = 10, d²p/dx² = -3/2 <0

So, x = 10 is the point of local maxima

Hence, the profit is maximum only if the daily output is 10.

问题36.制造商可以以每件(5 – x / 100)的价格出售x件物品。费用价格为(x / 5 + 500)。找到他应该出售以赚取最大利润的物品数量。

解决方案：

Let us considered S(x) be the selling price of x items and C(x) be the cost price of x items.

So, it is given that

S(x) = (5 – x/100) = 5x – x²/100

and            

C(x)= x/5 + 500

Then the profit function is 

P(x) = S(x) – C(x) 

= 5x – x²/100 -x/5 – 500 = 24x/5 – x²/100 – 500

On differentiating w.r.t. x, we get

P'(x) = 24/5 – x/50

Also p”(x) = – 1/50

For maxima and minima,

Put, P'(x) = 0

⇒ 24/5 – x/50 = 0

⇒ x = 24/5 × 50 = 240

When x = 240, P”(240) = -1/50 < 0

So, x = 240 is a point of maxima.

Hence, when the manufacturer sells 240 then he can earn maximum profit.

问题37.敞开式水箱的建造应具有正方形的底部和垂直的侧面，以容纳一定量的水。如果将深度设为宽度的一半，则表明用铅做衬的费用最少。

解决方案：

Let us considered l be the length of side of square base of the tank and h be the height of tank.

So, the volume of tank is 

V = l²h  ……(i)

And the total surface area is 

A = l² + 4lh  …..(ii)

Now,

From eq(i) and (ii), we get

A = l² + 4v/l

On differentiating w.r.t. l, we get

dA/dl = 2l – 4v/l²

Also, d²A/dl² = 2 + 8v/l³

For maxima and minima,

Put, dA/dl = 0

⇒ 2l – 4v/l² = 0

⇒ 2l³ – 4v = 0

⇒ l³ = 2v = 2t²h

⇒ l²[ l – 2h ]= 0

⇒ l = 0 or 2h

Here, l = 0 is not possible

At l = 2h, d²S/dl² > 0      

So, l = 2h is point of local minima

Hence, the total surface area is minimum when l = 2h

问题38.容积为c的盒子的长度应为宽度的两倍。顶部和四个侧面的材料每平方米的成本是底部的三倍。最经济的方面是什么?

解决方案：

Let us considered ABCDEFGH be a box of constant volume c and it is given that the box is twice as long as its width.

So, BF = x and AB = 2x

So, the cost of material of top and front side = 3 x cost of material of the bottom of the box.

⇒ 2x × x + xh + xh+ 2xh + 2xh = 3 × 2x²

⇒ 2x² + 2xh + 4xh = 6x²

⇒ 4x² – 6xh = 0

⇒ 2x(2x – 3h) = 0

⇒ x = 3h/2 or h = 2x/3

Volume of box is 

V = 2x × x × h

c = 2x²h

h = c/2x²                           ……(i)

Now,

The surface are of the box is 

A = 2 (2x² + 2xh + xh)

= 2(2x² + 3xh)

= 2(2x² + 3xc/2x²)

= 2(2x² + 3/2 × c/x)

On differentiating w.r.t. x, we get

dA/dx = 2(4x – 3/2 × c/x²)

For maxima and minima,

Put dA/dx = 0

2(4x – 3/2 × c/x²) = 0

8x³ – 3c = 0

x = (3c/8)^1/3

When x = (3c/8)^1/3, d²A/dx² = 2 (4 + 3 × C/x³) > 0  

So, x = (3c/8)^1/3 is point of local minima

Hence, the most economic dimension will be

x = width = (3c/8)^1/3

2x = length = 2(3c/8)^1/3

h = height = 2x/3 = 2/3 × (3c/8)^1/3

问题39.给出了一个球体和一个立方体的表面积之和，表明当它们的体积之和最小时，球体的直径等于立方体的边缘。

解决方案：

Lets us considered S be the sum of the surface areas of a sphere and a cube.

S = 4πr² + 6l²       …..(i)

Here, I be the side of the cube and r be the radius of the sphere

And V be the volume of sphere and cube

V = 4/3πr³ + l³       …..(ii)

$I=\sqrt{\frac{S-4πr^2}{6}}$

$V=4/3πr^2+(\frac{S-4πr^2}{6})^\frac{3}{2}$

On differentiating w.r.t. r, we get

$\frac{dV}{dr}=4πr^2+\frac{3}{2}(\frac{s-4πr^2}{6})^\frac{1}{2} (\frac{-4π}{6})^{2r}$

For maxima and minima,

Put dV/dr = 0

⇒ 4πr² = π/6(S – 4πr²)^1/2 × 2r = 0

⇒ 2rπ[2r – I] = 0

r = 0, l/2

Now,

$\frac{d^2V}{dr^2}=8πr-\frac{2π}{√6}[(S-4πr^2)^{\frac{1}{2}}]-\frac{8πr^2}{2(S-4πr^2)^{\frac{1}{2}}}$

At r = I/2, d²V/dr² > 0

So, r = I/2 is point of local minima

Hence, the volume is minimum when l = 2r

问题40.将一定量的金属铸造成具有矩形底和半圆形端部的半圆柱体。表明为了使总表面积最小，圆柱体的长度与其半圆形端部的直径之比为π：(π+ 2)

解决方案：

Let ABCDEF be a half cylinder with rectangular base and semicircular ends.

So, AB = height of the cylinder = h

Let us considered r be the radius of the cylinder.

As we know that the volume of the half cylinder is 

V = 1/2πr²h

2V/πr² = h

The total surface area of the half cylinder is

A = LSA of the half cylinder + area of two semicircular ends + area of the rectangle (base)

A = πrh + πr²/2 + πr²/2 +h²r

= (πr + 2r)h + πr²

= (π + 2)2v/πr + πr²

On differentiating w.r.t. r, we get

dA/dr = [(π + 2)2v/π(-1/r²) + 2πr]

For maxima and minima,

Put dA/dr = 0 

⇒ [(π + 2)2v/π(-1/r²) + 2πr] = 0 

⇒ [(π+2)2v/πr² = 2πr

But 2r = D

h : D = π : π + 2

Again differentiating w.r.t. r, we get

d²A/dr² = (π + 2)v/π × 2/r³ + 2π > 0

So, S will be minimum when h : 2r is π : π-12.

Hence, the height of the cylinder : Diameter of the circular end π : π + 2

问题41.梁的强度随其宽度和深度平方的乘积而变化。找出可以从半径为a的圆对数切下的最强光束的尺寸?

解决方案：

Let us considered ABCD be the cross-sectional area of the beam which is cut from a circular log of radius a.

So, AO = a and AC = 2a

Let x be the width and y be the depth of log. Also, S be the strength of the beam 

According to the question,

S = xy²      …..(i)

In ΔABC

x² + y² = (2a)²

⇒ y = (2a)² – x²       …..(ii)

From eq(i) and (ii), we get

S = x((2a)² – x²)

On differentiating w.r.t. x, we get

⇒ dS/dx = (4a² – x²) – 2x²

⇒ dS/dx = 4a² – 3x²

For maxima or minima

Put, dS/dx = 0

⇒ 4a² – 3x² = 0

⇒ x² = 4a²/3

x = 2a√3

Now put the value of x in eq(ii)

y² = 4a² – 4a²/3 = 8a²/3

y = 2a×√(2/3)

Now, 

At x = 2a/√3, y = √(2/3)2a, d²S/dx² = -6x = -12a/√3 < 0

So, (x = 2a/√3, y = √(2/3)2a) is the point of local maxima.

Hence, the dimension of the strongest beam is 2a/√3 and √(2/3)2a.

问题42.通过给定点P(1，4)画一条直线。确定坐标轴上截距之和的最小值。

解决方案：

Let us considered l be a line through the point P (1, 4) that cuts the x-axis and y-axis.

So, the equation of line(l) is 

y – 4 = m(x – 1)

x-Intercept is (m – 4)/m and y-intercept is (4-m)

Let S = (m – 4)/m + 4 – m

On differentiating w.r.t. m, we get

dS/dm = 4/m² – 1

For maxima and minima,

Put, dS/dm = 0

⇒ 4/m² -1 = 0

⇒ m = ±12

Now,

d²S/dm² = -8/m³

At m = 2, d²S/dm² = -1 < 0

At m = -2, d²S/dm²= 1 > 0

So, m = -2 is point of local minima.

Hence, the least value of sum of intercept is

= (m – 4)/m + 4 – m

= 3 + 6 = 9

问题43.页面的总面积为150 cm ² 。顶部和底部的边距组合宽度为3厘米，侧面为2厘米。页面的尺寸必须是多少才能使印刷品的最大面积?

解决方案：

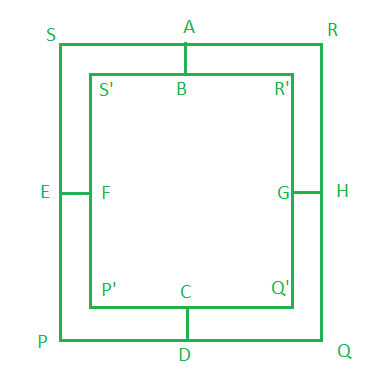
Given that the area of the page PQRS in 150 cm²

Also, AB + CD = 3 cm

EF + GH = 2 cm

Let us considered x and y be the combined width of margin at the top and bottom and the sides

x = 3 cm and y = 2 cm.

Now, we find the area of printed matter = area of P’Q’R’S’

⇒ A = P’Q’ Q’R’

⇒ A = (b – y)(l – x)

⇒ A = (b – 2)(l – 3)          …..(i)

Also,

The area of PQRS = 150 cm²

⇒ lb = 150                  …..(ii)

From eq(i) and (ii), we get

A = (b – 2)(150/b – 3)

On differentiating w.r.t. b, we get

dA/db = (150/b – 3) + (b – 2)(- 150/b²)

For maximum and minimum,

Put dA/db = 0

⇒ (150 – 3b)/b + (-150)(b – 2)b² = 0

⇒ 150b – 3b² – 150b +300 = 0

⇒ -3b² + 300 = 0

⇒ b = 10

From eq(ii), we get

l = 15

Now,

d²A/db² = -150/b2 – 150[-1/b2 + 4/b3]

When b = 10, d²A/db² = -15/10 – 150[-1/100 + 4/1000] = -1.5 + 9 = -0.6 < 0

So, b = 10 is point of local maxima.

Hence, the required dimension will be 15 cm and 10 cm.

问题44.粒子在直线中移动在时间t中描述的空间s为s = t ⁵ – 40t ³ + 30t ² + 80t –250。求出加速度的最小值。

解决方案：

Given that s is the space in time t by a moving particle is 

S = t⁵ – 40t³ +30t² +80t – 250

Velocity = dS/dt = 5t⁴ -120t² + 60t + 80

Acceleration = a = d²S/dt² = 20t³ – 240t + 60t           …..(i)

Now,

da/dt = 60t² – 240

For maxima and minima,

Put, da/dt = 0

⇒ 60t² – 240 = 0

⇒ 60(t² – 4) = 0

⇒ t = 2

Now,

d²a/dt² = 120t

At t = 2, d²a/dt² = 240 > 0

So, t = 2 is point of local minima

Hence, the minimum acceleration is 160 – 480 + 60 = -260 

2吨³ +4吨² – – 7时它的速度是最大和最小加速度找到直线运动，使得问题45.一种粒子其在任何时刻t距离s为s = T4^分之4给出。

解决方案：

Given that 

Distance(S) = t⁴/4 – 2t³ + 4t² – 7

Velocity(V) = dS/dt = t³ – 6t² + 8t

Acceleration(a) = d²S/dt² = 3t² – 12t + 8

For velocity to be maximum and minimum,

Put dV/dt = 0

⇒ 3t² – 12t +8 = 0

⇒ t = $\frac{12±\sqrt{144-96}}{6}$

= 2 ± 4√3/6

t = (2 + 2/√3), (2 – 2/√3)

Now,

d²V/dt² = 6t – 12

At t = (2 – 2/√3), d²V/dt² = 6(2 – 2/√3) – 12 = -12/√3  < 0

t = (2 + 2/√3), d²V/dt² = 6(2 + 2/√3) – 12 = 12/√3  > 0

So, at t = (2 – 2/√3), velocity is maximum

For acceleration to be maximum and minimum

Put da/dt = 0

⇒ 6t – 12 = 0

⇒ t = 2

Now,

When, t = 2, d²a/dt² = 6 > 0

Hence, at t = 2, acceleration is minimum.