第12类RD Sharma解决方案–第18章，最大值和最小值–练习18.3

问题1.找到以下函数的局部最大值或局部最小值的点以及相应的局部最大值和局部最小值。另外，找到拐点，如果有的话：

(i)f(x)= x ⁴ – 62x ² + 120x + 9

解决方案：

Given function: f(x) = x⁴ – 62x² + 120x + 9

Differentiating with respect to x

f'(x) = 4x³ – 124x + 120 = 4(x³ – 31x + 30)

Again differentiating with respect to x

f”(x) = 12x² – 124 = 4(3x² – 31)

Now, for maxima and minima  

Put f'(x) = 0

⇒ 4(x³ – 31x + 30) = 0

⇒ x³ – 31x + 30 = 0

⇒ x = 5, 1, -6

Now,

f”(5) = 176 > 0

⇒ x = 5 is point of local minima  

f”(1) = -112 < 0

⇒ x = 1 is point of local maxima  

f”(-6) = 308 > 0

⇒ x = -6 is point of local minima  

Now, we find the local maximum value = f(1) = 68

and local minimum value = f(5) = -316

and = f(-6) = -1647

(ii)f(x)= x ³ – 6x ² + 9x + 15

解决方案：

Given function: f(x) = x³ – 6x² + 9x +15

Differentiating with respect to x

f'(x) = 3x² -12x + 9 = 3(x² – 4x + 3)

Again differentiating with respect to x

f”(x) = 6x – 12

Now, for maxima and minima  

Put f'(x) = 0

⇒ 3(x² – 4x + 3) = 0

⇒ x² – 4x + 3 = 0

⇒ (x – 3)(x – 1) = 0

⇒ x = 3, 1  

Now,

f”(3) = 6 > 0

⇒ x = 3 is point of local minima  

f”(1) = -6 < 0

⇒ x = 1 is point of local maxima  

⇒ x = -6 is point of local minima  

Now we find the local maximum value = f(1) =19

and local minimum value = f(3) = 15                                  

(iii)f(x)=(x – 1)(x + 2) ²

解决方案：

Given function: f(x) = (x – 1)(x + 2)²

Differentiating with respect to x

f ‘(x) = (x + 2)² + 2(x – 1)(x + 2)

= (x + 2)(x + 2 + 2x – 2)

= (x + 2)(3x)

Again differentiating with respect to x

f ”(x) = 3(x + 2) + 3x

= 6x + 6

For maxima and minima  

Put f'(x) = 0

⇒ 3x(x + 2) = 0

⇒ x = 0, -2  

Now,

f”(0) = 6 > 0

⇒ x = 0 is point of local minima  

f”(-2) = -6 < 0

⇒ x = -2 is point of local maxima  

Now we find the local maximum value = f(-2) =0

Local minimum value = f(0) = -4                

(iv)f(x)= 2 / x – 2 / x ² ，x> 0

解决方案：

Given function: f(x) = 2/x – 2/x², x > 0

Differentiating with respect to x

f'(x) = -2/x² + 4/x³

Again differentiating with respect to x

f”(x) = -4/x³ – 12/ x⁴

For maxima and minima  

Put f'(x) = 0

⇒ -2/x² + 4/x³ = 0

⇒ -2(x – 2)/x³ = 0 

⇒ x = 2  

Now,

f”(2) = 4/8 – 12/6 = 1/2 – 3/4 = -1/4 < 0

⇒ x = 2 is point of local maxima   

Now, local maximum value = f(2) = 1/2

[v)f(x)= xe ^x

解决方案：

Given function: f(x) = xe^x

Differentiating with respect to x

f'(x) = e^x + xe^x = e^x(x + 1) 

Again differentiating with respect to x

f”(x) = e^x(x + 1) + e^x = e^x(x + 2) 

For maxima and minima  

Put f'(x) = 0

⇒ e^x(x + 1) = 0

⇒ x = -1

Now,

f”(-1) = e^-1 = 1/e > 0

⇒ x = -1 is point of local minima

Now, local minimum value = f(-1) = -1/e

(vi)f(x)= x / 2 + 2 / x，x> 0

解决方案：

Given function: f(x) = x/2 + 2/x, x > 0

Differentiating with respect to x

f'(x) = 1/2 – 2/x²

Again differentiating with respect to x

f”(x) = 4/x³

For maxima and minima  

Put f'(x) = 0

⇒ 1/2 – 2/x² = 0

⇒ (x² – 4)/2x² = 0

⇒ x = -2, +2  

Now,

f”(2) = 4/8 = 1/2 > 0

Thus, x = 2

x=-2 not taken because x > 0 is given. 

Now, local minimum value = f (2) = 2

(vii)f(x)=(x +1)(x + 2) ^1/3 ，x≥-2

解决方案：

Given function: f(x) = (x + 1)(x + 2)^1/3, x ≥ -2

Differentiating with respect to x

f ‘(x) = (x + 2)^1/3 + 1/3(x + 1)(x + 2)^-2/3

= (x + 2)^-2/3(x + 2 + 1/3(x + 1))

= 1/3(x + 2)^-2/3(4x + 7)

Again differentiating with respect to x

f”(x) = -2/9(x + 2)^-5/3(4x + 7) + 1/3(x + 2)^-2/3 × 4 

For maxima and minima  

Put f'(x) = 0

⇒ 1/3(x + 2)^-2/3(4x + 7) = 0

⇒ (4x + 7) = 0

⇒ x = -7/4

Now,

f “(-7/4) = 4/3(-7/4 + 2)^-2/3 

Thus, x = -7/4 is point of local minima

Now, local minimum value = f(-7/4) = $\frac{-3}{4^\frac{4}{3}}$

(viii)f(x)= x $\sqrt{32-x^2}$ ，-5≤x≤5

解决方案：

Given function: f(x)=x$\sqrt{32-x^2}$, -5 ≤ x ≤ 5

Differentiating with respect to x

f'(x) = $\sqrt{32-x^2}+\frac{x}{2\sqrt{32-x^2}}$× (-2x)

= $\frac{2(32-x^2)-2x^2}{2\sqrt{32-x^2}}$

= $\frac{64-4x^2}{2\sqrt{32-x^2}}$

Again differentiating with respect to x

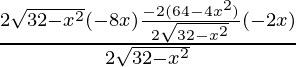
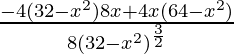
f”(x) = $\frac{2\sqrt{32-x^2}×(-8x)\frac{-2(64-4x^2)}{2\sqrt{32-x^2}}×(-2x)}{2\sqrt{32-x^2}}$

= $\frac{-4(32-x^2)8x+4x(64-x^2)}{8(32-x^2)^\frac{3}{2}}$  

For maxima and minima  

Put f'(x) = 0

⇒ $\frac{64-4x^2}{2\sqrt{32-x^2}}$= 0

⇒ 64 – 4x² = 0

⇒ x = ±4

Now,

f”(4) = $\frac{-4(32-16)32+16(64-16)}{8(32-16)^{3/2}}$<0

Thus, x = 4 is point of maxima

Now, local maximum value = f(4) = 16

x = -4 is point of minima

Now, local minimum value = f(-4) = -16

(ix)f(x)= x ³ – 2ax ² + a ² x，a> 0，x∈R

解决方案：

Given function: f(x) = x³ – 2ax² + a²x

Differentiating with respect to x

f ‘(x) = 3x² – 4ax + a²

Again differentiating with respect to x

f”(x) = 6x – 4a

For maxima and minima  

Put f'(x) = 0

⇒ 3x² – 4ax + a² = 0

⇒ x = $\frac{4a±\sqrt{16a^2-12a^2}}{6}$

= (4a ± 2a)/6 = a, a/3

Now, 

f”(a) = 2a > 0 as a > 0

x = a is point of local minima

f”(a/3) = -2a < 0 as a < 0

x = a/3 is point of local maxima

Hence,

The local maximum value = f(a/3) = 4a³/27

and local minimum value = f(a) = 0

(x)f(x)= x + a ² / x，a> 0，x≠0

解决方案：

Given function: f(x) = x + a²/x

Differentiating with respect to x

f’ (x) = 1 – a²/x²

Again differentiating with respect to x

f”(x) = 2a²/x³

For maxima and minima  

Put f'(x) = 0

⇒ 1 – a²/x² = 0

⇒ x² – a² = 0

x = ± a

Now,

f”(a) = 2/a > 0 as a > 0

x = a is point of minima

f”(-a) = -2/a < 0 as a > 0

x = -a is point of maxima

Hence, the local maximum value = f(-a) = -2a

and local minimum value = f(a) = 2a

(xi)f(x)= 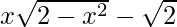$x\sqrt{2-x^2} -\sqrt{2}$ ，-√2≤X≤√2

解决方案：

Given function: f(x) = $x\sqrt{2-x^2}$

Differentiating with respect to x

f'(x) = $\sqrt{2-x^2} -\frac{2x^2}{x\sqrt{2-x^2} }$

= $\frac{2(2-x^2)-2x^2}{2\sqrt{2-x^2}}$

 = $\frac{2-2x^2}{\sqrt{2-x^2}}$

Again differentiating with respect to x

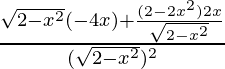
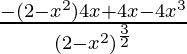
f”(x) = $\frac{\sqrt{2-x^2}(-4x)+\frac{(2-2x^2)2x}{\sqrt{2-x^2}}}{(\sqrt{2-x^2})^2}$

= $\frac{-(2-x^2)4x+4x-4x^3}{(2-x^2)^\frac{3}{2}}$

For maxima and minima  

Put f'(x) = 0

⇒ $\frac{2(1-x^2)}{\sqrt(2-x^2)}=0$

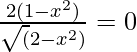
⇒x = ±1

Now,  

f”(1) < 0

⇒ x = 1 is point of local maxima

f”(-1) > 0

⇒ x = -1 is point of local maxima

Hence, the local maximum value = f (1) = 1

and local minimum value = f (-1) = -1

(xii) $f(x) = x+ \sqrt{1-x}$ ，x≤1

解决方案：

Given function: f(x) = x + $\sqrt{1-x}$

Differentiating with respect to x

f'(x) = $1-\frac{1}{2\sqrt{1-x}}=\frac{2\sqrt{1-x}-1}{2\sqrt{1-x}}$

f'(x) = $\frac{2\sqrt{1-x}(\frac{-1}{\sqrt{1-x}})+\frac{2\sqrt{1-x}-1}{\sqrt{1-x}}}{4(1-x)}$

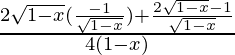
For maxima and minima  

Put f'(x) = 0

⇒ $\frac{2\sqrt{1-x}-1}{2\sqrt{1-x}}=0$

⇒ $\sqrt{1-x}$=1/2

⇒ x= 1 – 1/4 = 3/4

Now,

f”(3/4) < 0

⇒ x = 3/4 is point of local maxima

Hence, the local maximum value = f (3/4) = 5/4

问题2。找到以下函数的局部极值：

(i)f(x)=(x – 1)(x – 2) ²

解决方案：

Given function: f(x) = (x – 1)(x – 2)²

Differentiating with respect to x

f'(x) = (x – 2)² + 2(x – 1)(x – 2)

= (x – 2)(x – 2 + 2x – 2)

= (x – 2)(3x – 4)

Again differentiating with respect to x

f”(x) =(3x – 4) + 3(x – 2)

For maxima and minima  

Put f'(x) = 0

⇒ (x – 2)(3x – 4) = 0

⇒ x = 2, 4/3

Now,

f”(2) > 0

x = 2 is local minima

f “(4/3) = -2 < 0

x = 4/3 is point of local maxima

Hence, the local maximum value = f(4/3) = 4/27

and the local minimum value = f(2) =0    

(ii)f(x)= x 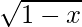$\sqrt{1-x}$ ，x≤1

解决方案：

Given function: f (x) = x$\sqrt{1-x}$

Differentiating with respect to x

f ‘(x) = $\sqrt{1-x}+\frac{x}{2\sqrt{1-x}}(-1)$

= $\frac{2(1-x)-x}{2\sqrt{1-x}}$

= (2 – 3x)/2$\sqrt{1-x}$

Again differentiating with respect to x

f”(x) = 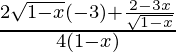$\frac{2\sqrt{1-x}(-3)+\frac{2-3x}{\sqrt{1-x}}}{4(1-x)}$

For maxima and minima  

Put f'(x) = 0

⇒ (2 – 3x)/2$\sqrt{1-x}$=0

⇒ x = 2/3

Now,

f “(2/3) < 0

x = 2/3 is point of maxima

Hence, the local maximum value = f (2/3) = 2/3√3

(iii)f(x)=-(x – 1) ³ (x +1) ²

解决方案：

Given function: f(x) = -(x – 1)³(x + 1)²  

Differentiating with respect to x

  f ‘(x) = -3(x – 1)² (x + 1)² – 2(x – 1)³ (x + 1)  

= -(x – 1)² (x + 1) (3x + 3 + 2x – 2)

= -(x – 1)²(x + 1) (5x + 1)

Again differentiating with respect to x

f”(x) = -2(x – 1) (x + 1) (5x + 1) – (x – 1)² (5x + 1) – 5 (x – 1)² (x + 1)

For maxima and minima  

Put f'(x) = 0

⇒ -(x – 1)² (x + 1) (5x + 1) = 0

⇒ x = 1, -1, -1/5

Now,

f”(1) = 0

x = 1 is inflection point

f “(-1) = -4 × -4 = 16 > 0

x = -1 is point of minima

f”(-1/5) = -5(36/25) × (4/5) = -144/25 < 0

x = -1/5 is point of maxima

Hence, the local maximum value = f (-1/5) = 3456/3125

and the local minimum value = f (-1) = 0

问题3.函数y = a log x + bx ² + x在x = 1和x = 2处具有极值。找到a和b。

解决方案：

We have,

y = alogx + bx² + x

Differentiating with respect to x

dy/dx = a/x + 2bx + 1

Again differentiating with respect to x

d²y/dx² = -a/x² +2b

For maxima and minima  

Put dy/dx = 0

⇒ a/x + 2bx +1 = 0

Given that extreme value exist at x = 1, 2

⇒ a + 2b = -1        …..(i)

a/2 + 4b = -1

⇒ a + 8b = -2       …..(ii)

On solving eq(i) and (ii), we get

a = -2/3, b = -1/6

问题4.证明(log x / x)在x = e处有一个最大值。

解决方案：

Given function: f(x) = logx / x

Differentiating with respect to x

f'(x)$=\frac{x(1/x)-logx}{x^2}=\frac{1-logx}{x^2}$

Now, f'(x) = 0

⇒ 1 – logx = 0

⇒ logx = 1

⇒ logx = loge

⇒ x = e

Again differentiating with respect to x

$f ''(x)=\frac{x^2(-1/x)-(1-logx)(2x)}{x^4}$

$=\frac{-x-2x(1-logx)}{x^4}$

= $\frac{-3+2logx}{x^3}$

Now, f ”(e) = $\frac{-3+2loge}{e^3}$

=(-3 + 2)/e³ = -1/e³ < 0

Therefore, by second derivative test, f is the maximum at x = e.

问题5.找到函数f(x)= 4 /(x + 2)+ x的最大值和最小值。

解决方案：

Given function: f(x) = 4/(x + 2) + x

Differentiating with respect to x

f'(x) = -4/(x + 2)² + 1

Again differentiating with respect to x

f”(x) = 8/(x + 2)³

For maxima and minima  

Put f'(x) = 0

⇒ -4/(x + 2)² + 1 = 0

⇒ (x + 2)² = 4

⇒ x² + 4x = 0

⇒ x (x + 4) = 0

 x = 0, -4

Now,

f ”(0) = 1 > 0

x = 0 is point of minima

f ”(-4) = -1 < 0

x = -4 is point of maxima

Hence, the local maximum value = f (-4) = -6

and the local minimum value = f (0) = 2

问题6.找到f(x)= tan x – 2x的最大值和最小值。

解决方案：

Given function: f(x) = tanx – 2x

Differentiating with respect to x

f'(x) = sec²x – 2

Again differentiating with respect to x

f”(x) = 2sec²x tanx

For maxima and minima  

Put f'(x) = 0

⇒ sex²x = 2

⇒ secx = ±√2

⇒ x = π/4, 3π/4

f”(π/4) = 4 > 0

x = π/4 is point of minima

f”(3π/4) = -4 < 0

x = (3π/4) is point of maxima

Hence, the maximum value = f (3π/4) = -1 – 3π/2

and the minimum value = f (π/4) = 1 – π/2

问题7.如果f(x)= x ³ + ax ² + bx + c在x = -1处有最大值，在x = 3处有最小值。确定a，b和c。

解决方案：

Given function: f(x) = x³ + ax² + b x + c

Differentiating with respect to x

f ‘(x) = 3x² + 2ax + b

It is given that f (x) is maximum at x = -1

f ‘(-1) = 3(-1)² + 2a(-1) + b = 0

f ‘(-1) = 3 – 2a + b = 0     …….(i)

At x = 3, f(x) is minimum 

f ‘(3) = 3(3)² + 2a(3) + b = 0

⇒ f ‘(3) = 27 + 6a +b = 0     …..(ii)

On solving eq(i) and (ii), we get

a = -3 and b = -9

Since f ‘(x) is independent of constant c, so, it can be any real number.