问题1.四边形的角度为3:5:9:13。找到所有四边形的角度。
解决方案:
As we know that, the sum of the angles of a quadrilateral is 360° (Angle sum property of quadrilateral)
As they are in ratio 3 : 5 : 9 : 13, so we can assume angles be as 3x, 5x, 9x and 13x.
So,
3x + 5x + 9x + 13x = 360°
30x = 360°
x = 360/30 = 12°
So the angles will be as follows:
3x = 3×12 = 36°
5x = 5×12 = 60°
9x = 9×12 = 108°
13x = 13×12 = 156°
Hence, the angles of quadrilateral are 36°, 60°, 108° and 156°.
问题2.如果平行四边形的对角线相等,则表明它是一个矩形。
解决方案:
As mentioned parallelogram, so let PQRS be a parallelogram
where, given
PR = QS

In ∆PQR and ∆QRS,
PR = QS …………………[Given]
PQ = RS …………………[Opposite sides of a parallelogram]
QR = RQ …………………[Common side]
∴ ∆PQR ≅ ∆QRS [By SSS congruency]
so, ∠PQR = ∠QRS [By C.P.C.T.] ………………………………………….(1)
Now, PQ || RS and QR is a transversal. …………………….[PQRS is a parallelogram]
∴ ∠PQR + ∠QRS = 180° [Co-interior angles of parallelogram]…………………………………… (2)
From (1) and (2), we have
∠PQR = ∠QRS = 90°
i.e., PQRS is a parallelogram having an angle equal to 90°.
Hence, PQRS is a rectangle. (having all angles equal to 90° and opposite sides are equal)
问题3:证明如果四边形的对角线彼此成直角平分,那么它就是菱形。
解决方案:
As mentioned quadrilateral, so let PQRS be a quadrilateral
where, given
PO = RO
SO = QO

In ∆POQ and ∆POS, we have
PO = PO [Common]
OQ = OS [O is the mid-point of QS]
∠POQ= ∠POS [Each 90°]
∴ ∆POQ ≅ ∆POS [By, SAS congruency]
∴ PQ = PS [By C.P.C.T.] …….. (1)
Similarly, PQ = QR …………………..(2)
QR = RS ……………………………………..(3)
RS = SP ………………………………………(4)
∴ From (1), (2), (3) and (4), we have
PQ = QR = RS = SP
Thus, the quadrilateral PQRS is a rhombus.
Alternative Solution:
So as it is given that diagonals of a quadrilateral PQRS bisect each other
According to Theorem 8.7 NCERT it is a parallelogram
PQRS can be proved first a parallelogram then proving one pair of adjacent sides equal will result in rhombus.
In ∆POQ and ∆POS, we have
PO = PO [Common]
OQ = OS [O is the mid-point of QS]
∠POQ= ∠POS [Each 90°]
∴ ∆POQ ≅ ∆POS [By,SAS congruency]
∴ PQ = PS [By C.P.C.T.] …….. (1)
Similarly, PQ = QR …………………..(2)
QR = RS ……………………………………..(3)
RS = SP ………………………………………(4)
From (1), (2), (3) and (4), we have
PQ = QR = RS = SP
Hence, as a parallelogram has all sides equal then it is called a rhombus.
问题4.证明正方形的对角线相等,并且彼此成直角平分。
解决方案:
As it is mentioned that it is a square so,
all sides are equal. (PQ = QR = RS = SP)
all angles at four corners = 90°
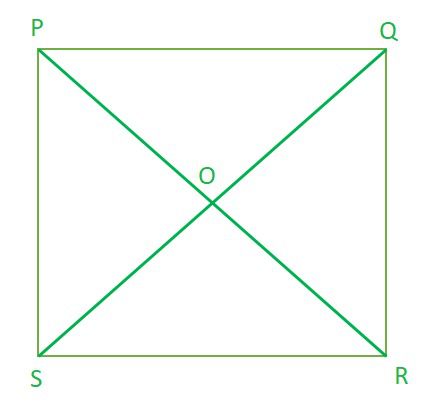
So, to prove that the diagonals are equal, we need to prove PR = QS.
In ∆PQR and ∆QPS, we have
PQ = QP ……………….[Common]
PS = PQ ………………..[Sides of a square PQRS]
∠PQR = ∠QPS …….[Each angle is 90°]
∆PQR ≅ ∆QPS [By SAS congruency]
AC = BD [By C.P.C.T.] …(1)
Now as we know square is also a parallelogram
In ∆POQ and ∆ROS, we have
∠POQ = ∠ROS ……………….[Opposite angles of two intersecting lines]
PQ = RS ………………..[Sides of a square PQRS]
∠PQO = ∠RSO …….[Alternate interior angles are equal]
∆PQR ≅ ∆QPS [By ASA congruency]
OP = OQ = OR = OS (Hence the diagonals are equal and bisect each other)
Now , In ∆OQP and ∆OSP, we have
OQ = OS [Proved]
QP = SP [Sides of a square PQRS]
OP = OP [Common]
∆OQP ≅ ∆OSP [By SSS congruency]
∠POQ = ∠POS [By C.P.C.T.] …(3)
∠POQ + ∠POS = 180° (∵ ∠POQ and ∠POS form a linear pair)
∠POQ = ∠POS = 90° [By(3)]
PR ⊥ QS …(4)
From (1), (2) and (4), we get PR and QS are equal and bisect each other at right angles (90°).
问题5:证明如果四边形的对角线相等,并且以直角彼此平分,则它是一个正方形。
解决方案:
As it is mentioned Quadrilateral, so let PQRS be a quadrilateral
where,
PR = QS
OP = OR = OQ = OS
∠POQ = ∠QOR = ∠ROS = ∠SOP = 90°

Now, in ∆POS and ∆POQ, We have
∠POS = ∠POQ [Each 90°]
PO = PO [Common]
OS= OQ [ ∵ O is the midpoint of BD]
∆POS ≅ ∆POQ [By SAS congruency]
PS = PQ [By C.P.C.T.] …(1)
Similarly, we have
PQ = QR … (2)
QR = RS …(3)
RS = SP…(4)
From (1), (2), (3) and (4), we have
PQ = QR = RS = SP
Hence, Quadrilateral PQRS have all sides equal.
Now, In ∆POS and ∆ROQ, we have
PO = RO [Given]
OS = OQ [Given]
∠POS = ∠ROQ [Vertically opposite angles]
So, ∆POS ≅ ∆ROQ [By SAS congruency]
∠PSO = ∠RQO [By C.P.C.T.]
So as they form a pair of alternate interior angles.
PS || QR
Similarly, PQ || RS
PQRS is a parallelogram.
Parallelogram having all its sides equal is a rhombus.
PQRS is a rhombus.
Now, in ∆PQR and ∆QPS, we have
PR = QS [Given]
QR = SP [Proved]
PQ = QP [Common]
∆PQR ≅ ∆QPS [By SSS congruency]
∠PQR = ∠QPS [By C.P.C.T.] ……(5)
Since, PS || QR and PQ is a transversal.
∠PQR + ∠QPS = 180° .. .(6) [ Co – interior angles]
∠PQR = ∠QPS = 90° [By(5) & (6)]
So, rhombus PQRS is having corners angle equal to 90°.
Hence, PQRS is a square.
问题6.平行四边形ABCD的对角AC对分∠A(见图8.19)。显示
(i)将∠C也一分为二,
(ii)ABCD是菱形。
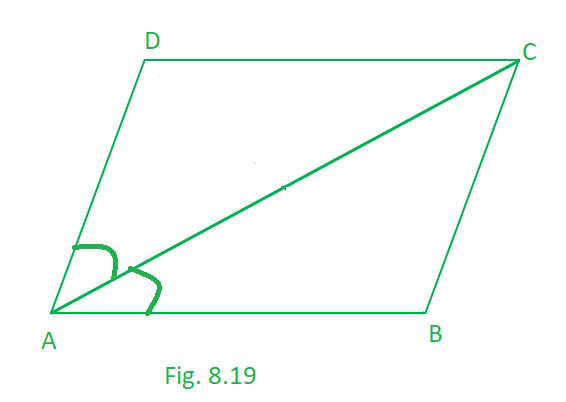
解决方案:
(i) As, ABCD is a parallelogram.
∠BAC = ∠DCA ……………………………(1) [Alternate interior angles are equal]
∠CAD = ∠BCA ………………………….(2) [Alternate interior angles are equal]
Also, ∠CAD = ∠CAB …………………….(3) [ (Given) as AC bisects ∠A]
From (1), (2) and (3), we have
∠DCA = ∠BCA
Hence, AC bisects ∠C.
(ii) In ∆ABC,
∠BAC = ∠DCA ………………………….. [Alternate interior angles are equal]
BC = AB …………………………….(4) [ Sides opposite to equal angles of a ∆ are equal]
Similarly, AD = DC ……..(5)
But, ABCD is a parallelogram. [Given]
AB = DC ………………….(6) (opposite sides of parallelogram)
From (4), (5) and (6), we have
AB = BC = CD = DA
As, ABCD is a parallelogram having all sides equal then it is a rhombus.
问题7. ABCD是菱形。证明对角AC二等分∠A和∠C,对角BD二等分∠B和∠D。
解决方案:
As, ABCD is a rhombus, so
AB = BC = CD = DA
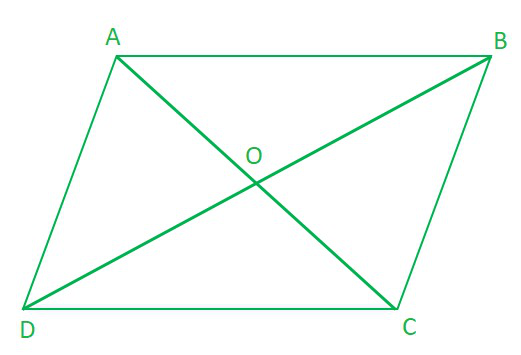
Now, As CD = AD
∠ADB= ∠ABD……………………….(1) [Angles opposite to equal sides of a triangle are equal]
∠ADB = ∠CBD …………………..(2) [ ∵ Alternate interior angles are equal] (Rhombus is a parallelogram)
From (1) and (2), we have
∠CBD = ∠ABD …………………..(3)
∠ABD= ∠CDB ……………………..(4) [ ∵ Alternate interior angles are equal]
From (1) and (4),
we have ∠ADB = ∠CDB
Hence, BD bisects ∠B as well as ∠D.
Similarly, we can prove that AC bisects ∠C as well as ∠A..
问题8. ABCD是一个矩形,其中对角线AC将∠A和∠C一分为二。表明:
(i)ABCD是一个正方形
(ii)BD对角线∠B和∠D。
解决方案:
There is rectangle ABCD such that AC bisects ∠A as well as ∠C, so
∠BAC = ∠DAC and,
∠DCA = ∠BCA ………………………………(1)

(i) As we know that every rectangle is a parallelogram.
ABCD is a parallelogram.
∠BCA = ∠DAC …………………….(2) [ Alternate interior angles are equal]
From (1) and (2), we have
∠DCA= ∠DAC……………………….(3)
In ∆ABC, ∠DCA= ∠DAC then,
CD = DA [Sides opposite to equal angles of a ∆ are equal]
Similarly, AB = BC
So, ABCD is a rectangle having adjacent sides equal.
ABCD is a square.
(ii) Since, ABCD is a square
AB = BC = CD = DA
so, In ∆ABD, as AB = AD
∠ABD = ∠ADB [Angles opposite to equal sides of a ∆ are equal]……………………..(1)
Similarly, ∠CBD = ∠CDB…………………..(2)
∠CBD = ∠ADB [Alternate interior angles are equal]………………(3)
From (1) and (3)
∠CBD = ∠ABD
From (2) and (3)
∠ADB = ∠CBD
So, BD bisects ∠B as well as ∠D.
问题9:在平行四边形ABCD中,在对角线BD上取两个点P和Q,使得DP = BQ(见图8.20)。显示 :
(i)ΔAPD≅ΔCQB
(ii)AP = CQ
(iii)ΔAQB≅ΔCPD
(iv)AQ = CP
(v)APCQ是平行四边形
解决方案:
ABCD is a parallelogram
DP = BQ
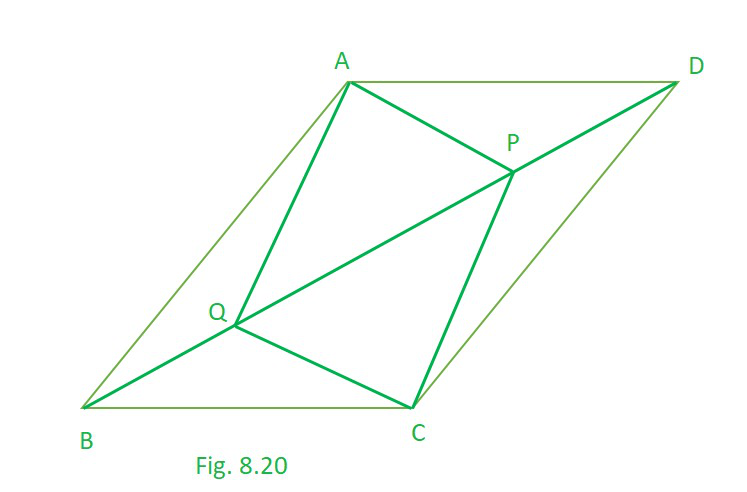
(i) As ABCD is a parallelogram
∠ADB = ∠CBD [Alternate interior angles are equal]……………….(1)
∠ABD = ∠CDB [Alternate interior angles are equal]…………………(2)
Now, in ∆APD and ∆CQB, we have
AD = CB [Opposite sides of a parallelogram ABCD are equal]
PD = QB [Given]
∠ADP = ∠CBQ [Proved]
Hence, ∆APD ≅ ∆CQB [By SAS congruency]
(ii) As, ∆APD ≅ ∆CQB [Proved]
AP = CQ [By C.P.C.T.]…………………(3)
(iii) Now, in ∆AQB and ∆CPD, we have
QB = PD [Given]
∠ABQ = ∠CDP [Proved]
AB = CD [ Opposite sides of a parallelogram ABCD are equal]
Hence, ∆AQB ≅ ∆CPD [By SAS congruency]
(iv) As, ∆AQB ≅ ∆CPD [Proved]
AQ = CP [By C.P.C.T.] …………………………..(4)
(v) In a quadrilateral APCQ,
Opposite sides are equal. [From (3) and (4)]
Hence, APCQ is a parallelogram. (NCERT Theorem 8.3)
问题10. ABCD是平行四边形,AP和CQ是对角线BD上顶点A和C的垂直线(见图8.21)。显示
(i)ΔAPB≅ΔCQD
(ii)AP = CQ
解决方案:
ABCD is a parallelogram
DP = BQ

(i) In ∆APB and ∆CQD, we have
∠APB = ∠CQD [Each 90°]
AB = CD [ Opposite sides of a parallelogram ABCD are equal]
∠ABP = ∠CDQ [Alternate angles are equal as AB || CD and BD is a transversal]
Hence, ∆APB ≅ ∆CQD [By AAS congruency]
(ii) As, ∆APB ≅ ∆CQD [Proved]
AP = CQ [By C.P.C.T.]
问题11:在∆ ABC和∆ DEF中,AB = DE,AB || DE,BC = EF和BC ||英孚顶点A,B和C分别与顶点D,E和F相连(见图8.22)。显示
(i)四边形ABED是平行四边形
(ii)四边形BEFC是平行四边形
(iii)广告|| CF和AD = CF
(iv)四边形ACFD是平行四边形
(v)AC = DF
(vi)∆ABC≅∆DEF。

解决方案:
AB = DE, and AB || DE,
BC = EF and BC || EF
(i) We have AB = DE and AB || DE [Given]
so here., ABED is a quadrilateral in which a pair of opposite sides (AB and DE) are parallel and of equal length.
Hence, ABED is a parallelogram.
(ii) BC = EF and BC || EF [Given]
i.e. BEFC is a quadrilateral in which a pair of opposite sides (BC and EF) are parallel and of equal length.
Hence, BEFC is a parallelogram.
(iii) as, ABED is a parallelogram [Proved]
∴ AD || BE and AD = BE …(1) [Opposite sides of a parallelogram are equal and parallel]
Also, BEFC is a parallelogram. [Proved]
BE || CF and BE = CF …(2) [Opposite sides of a parallelogram are equal and parallel]
From (1) and (2), we have
AD || CF and AD = CF
(iv) Since, AD || CF and AD = CF [Proved]
i.e., In quadrilateral ACFD, one pair of opposite sides (AD and CF) are parallel and of equal length.
Hence, Quadrilateral ACFD is a parallelogram.
(v) Since, ACFD is a parallelogram. [Proved]
So, AC =DF [Opposite sides of a parallelogram are equal]
(vi) In ∆ABC and ∆DEF, we have
AB = DE [Given]
BC = EF [Given]
AC = DE [Proved in (v) part]
∆ABC ≅ ∆DEF [By SSS congruency]
问题12. ABCD是一个梯形,其中AB || CD和AD = BC(见图8.23)。显示
(i)∠A=∠B
(ii)∠C=∠D
(iii)∆ABC≅∆BAD
(iv)对角线AC =对角线BD
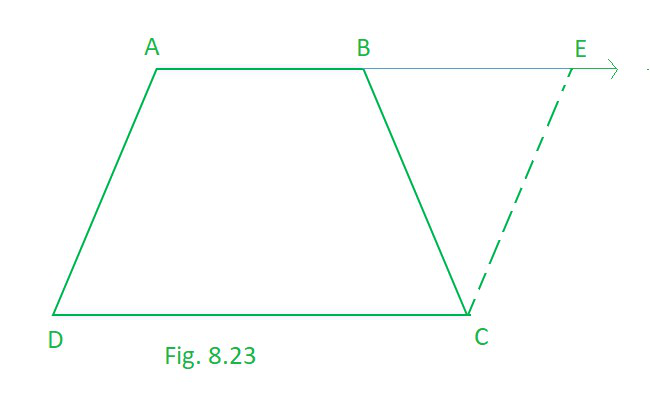
[提示:延伸AB并通过C线与与E处产生的AB相交的DA平行。
解决方案:
so basically here is a trapezium ABCD in which AB || CD and AD = BC.
Extended AB and draw a line through C parallel to DA intersecting AB produced at E

(i) AB || DC , AE || DC Also AD || CE
then, AECD is a parallelogram.
AD = CE …………………………(1) [Opposite sides of the parallelogram are equal]
But AD = BC …(2) [Given]
From (1) and (2),
BC = CE
Now, in ∆BCF, we have BC = CF
∠CEB = ∠CBE …(3) [Angles opposite to equal sides of a triangle are equal]
Also, ∠ABC + ∠CBE = 180° … (4) [Linear pair]
and ∠A + ∠CEB = 180° …(5) [Co-interior angles of a parallelogram ADCE]
From (4) and (5), we get
∠ABC + ∠CBE = ∠A + ∠CEB
∠ABC = ∠A [From (3)]
∠B = ∠A …(6)
(ii) AB || CD and AD is a transversal.
∠A + ∠D = 180° …(7) [Co-interior angles in parallelogram]
Similarly, ∠B + ∠C = 180° … (8)
From (7) and (8), we get
∠A + ∠D = ∠B + ∠C
∠C = ∠D [From (6)]
(iii) In ∆ABC and ∆BAD, we have
AB = BA [Common]
BC = AD [Given]
∠ABC = ∠BAD [Proved]
Hence, ∆ABC ≅ ∆BAD [By SAS congruency]
(iv) Since, ∆ABC ≅ ∆BAD [Proved]
AC = BD [By C.P.C.T.]