第17章理解形状的特殊四边形–练习17.1 |套装1
问题16.平行四边形的周长为150厘米。它的一侧比另一侧大25厘米。找到平行四边形的边的长度。
解决方案:
Given that,
Perimeter of the parallelogram = 150 cm
Let us assume that one of the sides as = ‘x’ cm
and other side as = (x + 25) cm
As we know that opposite sides of a parallelogram are parallel and equal.
Therefore, Perimeter = Sum of all sides
x + x + 25 + x + x + 25 = 150
4x + 50 = 150
4x = 150 – 50
x = 100/4 = 25
Hence, Sides of the parallelogram are (x) = 25 cm and (x+25) = 50 cm.
问题17:平行四边形的短边是4.8厘米,长边是短边的一半。找到平行四边形的周长。
解决方案:
Given that,
Shorter side of the parallelogram = 4.8 cm
and longer side of the parallelogram = 4.8 + 4.8/2 = 4.8 + 2.4 = 7.2cm
As we know that opposite sides of a parallelogram are parallel and equal.
Therefore, Perimeter = Sum of all sides
Perimeter of the parallelogram = 4.8 + 7.2 + 4.8 + 7.2 = 24cm
Hence, Perimeter of the parallelogram is 24 cm.
问题18:平行四边形的两个相邻角度为(3x-4)o和(3x + 10)°。找到平行四边形的角度。
解决方案:
As we know that adjacent angles of a parallelogram are equal.
Therefore, (3x – 4)° + (3x + 10)° = 180°
3x° + 3xo – 4 + 10 = 180°
6x = 180° – 6°
x = 174°/6 = 29°
The adjacent angles are,
(3x – 4)° = 3×29 – 4 = 83°
(3x + 10)° = 3×29 + 10 = 97°
As we know that Sum of adjacent angles = 180°
Hence, each angle is 83°, 97°, 83°, 97°.
问题19.在平行四边形ABCD中,对角线在O处一分为二。如果∠ABC= 30°,∠BDC= 10°和∠CAB= 70°。找:
∠DAB,∠ADC,∠BCD,∠AOD,∠DOC,∠BOC,∠AOB,∠ACD,∠CAB,∠ADB,∠ACB,∠DBC和∠DBA。
解决方案:
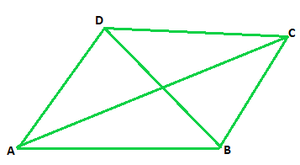
Given that,
∠ABC = 30°,
∠ABC = ∠ADC = 30° (We know that measure of opposite angles are equal in a parallelogram)
∠BDC = 10°
∠CAB =70°
∠BDA = ∠ADB = ∠ADC – ∠BDC = 30° – 10° = 20° (From figure we concluded)
∠DAB = 180° – 30° = 150°
∠ADB = ∠DBC = 20° (alternate angles)
∠BCD = ∠DAB = 150° (we know, opposite angles are equal in a parallelogram)
∠DBA = ∠BDC = 10° (we know, Alternate interior angles are equal)
In ΔABC ∠CAB + ∠ABC + ∠BCA = 180° (since, sum of all angles of a triangle is 180°)
70° + 30° + ∠BCA = 180°
∠BCA = 180° – 100° = 80°
∠DAB = ∠DAC + ∠CAB = 70° + 80° = 150°
∠BCD = 150° (opposite angle of the parallelogram)
∠DCA = ∠CAB = 70°
In ΔDOC ∠BDC + ∠ACD + ∠DOC = 180° (since, sum of all angles of a triangle is 180°)
10° + 70° + ∠DOC = 180°
∠DOC = 180°- 80°
∠DOC = 100°
Therefore, ∠DOC = ∠AOB = 100° (Vertically opposite angles are equal)
∠DOC + ∠AOD = 180° [Linear pair]
100° + ∠AOD = 180°
∠AOD = 180°- 100°
∠AOD = 80°
Therefore, ∠AOD = ∠BOC = 80° (Vertically opposite angles are equal)
∠CAB = 70o
∠ABC + ∠BCD = 180° (In a parallelogram sum of adjacent angles is 180°)
30° + ∠ACB + ∠ACD = 180°
30° + ∠ACB + 70° = 180°
∠ACB = 180° – 100°
∠ACB = 80°
Hence ∠DAB = 150o, ∠ADC = 30°, ∠BCD = 150°, ∠AOD = 80°, ∠DOC = 100°, ∠BOC = 80°, ∠AOB = 100°, ∠ACD = 70°, ∠CAB = 70°, ∠ADB = 20°, ∠ACB = 80°, ∠DBC = 20°, and ∠DBA = 10°.
问题20.找到标有问号的角度,如图所示。
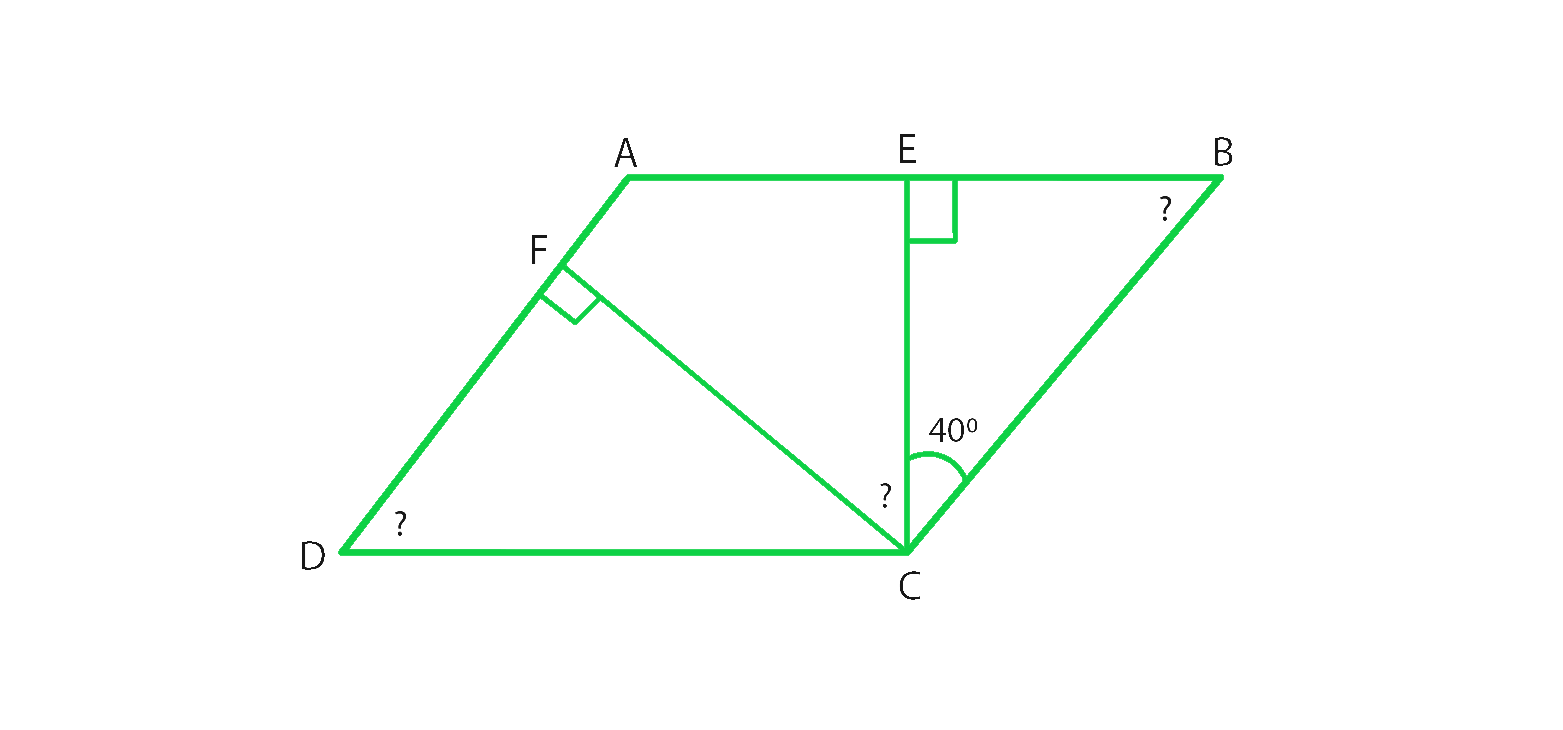
解决方案:
In ΔBEC ∠BEC + ∠ECB +∠CBE = 180° (Sum of angles of a triangle is 180°)
90° + 40° + ∠CBE = 180°
∠CBE = 180°-130°
∠CBE = 50°
∠CBE = ∠ADC = 50° (Opposite angles of a parallelogram are equal)
∠B = ∠D = 50° (opposite angles of a parallelogram are equal)
∠A + ∠B = 180° (Sum of adjacent angles of a triangle is 180°)
∠A + 50° = 180°
∠A = 180°-50°
therefore, ∠A = 130°
In ΔDFC ∠DFC + ∠FCD +∠CDF = 180° (Sum of angles of a triangle is 180°)
90° + ∠FCD + 50° = 180°
∠FCD = 180°-140°
∠FCD = 40°
∠A = ∠C = 130° (Opposite angles of a parallelogram are equal)
∠C = ∠FCE +∠BCE + ∠FCD
∠FCD + 40° + 40° = 130°
∠FCD = 130° – 80°
∠FCD = 50°
Hence ∠EBC = 50°, ∠ADC = 50° and ∠FCD = 50°.
问题21.通过平行四边形的钝角的同一顶点,平行四边形的海拔高度之间的夹角为60°。找到平行四边形的角度。
解决方案:

Let us consider parallelogram ABCD, where DP⊥ AB and DQ ⊥ BC.
Given that ∠PDQ = 60°
In quadrilateral DPBQ ∠PDQ + ∠DPB + ∠B + ∠BQD = 360° (Sum of all the angles of a Quadrilateral is 360°)
60° + 90° + ∠B + 90° = 360°
∠B = 360° – 240°
∠B = 120°
∠B = ∠D = 120° (Opposite angles of parallelogram are equal)
∠B + ∠C = 180° (Sum of adjacent interior angles in a parallelogram is 180°)
120° + ∠C = 180°
∠C = 180° – 120° = 60°
∠A = ∠C = 60° (Opposite angles of parallelogram are equal)
Hence, Angles of a parallelogram are 60°, 120°, 60°, 120°
问题22.在图中,ABCD和AEFG是平行四边形。如果∠C= 55°,theF的度量是多少?

解决方案:
From figure, we conclude that,
In parallelogram ABCD ∠C = ∠A = 55° (In a parallelogram opposite angles are equal in a parallelogram)
In parallelogram AEFG ∠A = ∠F = 55° (In a parallelogram opposite angles are equal in a parallelogram)
Hence ∠F = 55°
问题23.在图中,BDEF和DCEF均为平行四边形。 BD = DC是真的吗?为什么或者为什么不?
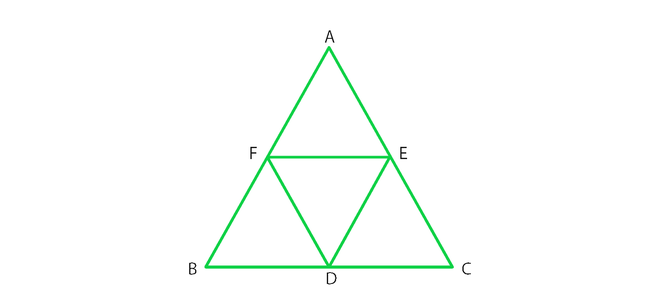
解决方案:
From figure, we conclude that,
In parallelogram BDEF BD = EF (In a parallelogram opposite sides are equal)
In parallelogram DCEF DC = EF (In a parallelogram opposite sides are equal)
Since, BD = EF = DC
Therefore, BD = DC
问题24.在图中,假设已知DE = DF。那么, ΔABC是等腰吗?为什么或者为什么不?

解决方案:
From figure we conclude that,
In parallelogram BDEF BD = EF and BF = DE (opposite sides are equal in a parallelogram)
In parallelogram DCEF DC = EF and DF = CE (opposite sides are equal in a parallelogram)
In parallelogram AFDE AF = DE and DF = AE (opposite sides are equal in a parallelogram)
therefore, DE = AF = BF
similarly, DF = CE = AE
Given that, DE = DF
Since, DF = DF
AF + BF = CE + AE
AB = AC
Hence, ΔABC is an isosceles triangle.
问题25.平行四边形ABCD的对角线在O处相交,如图所示。 XY包含O,X,Y是平行四边形相反侧的点。请说明以下各项的原因:
(i)OB =外径
(ii)∠OBY=∠ODX
(iii)∠BOY=∠DOX
(iv)ΔBOY=ΔDOX
现在,说明XY是否在O处被一分为二。
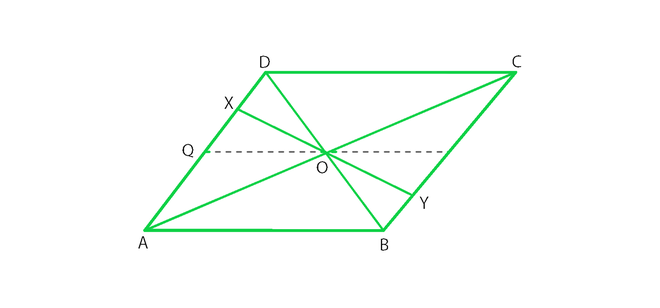
解决方案:
(i) OB = OD
OB = OD. Since diagonals bisect each other in a parallelogram.
(ii) ∠OBY =∠ODX
∠OBY =∠ODX. Since alternate interior angles are equal in a parallelogram.
(iii) ∠BOY= ∠DOX
∠BOY= ∠DOX. Since vertical opposite angles are equal in a parallelogram.
(iv) ΔBOY ≅ ΔDOX
ΔBOY and ΔDOX. Since OB = OD, where diagonals bisect each other in a parallelogram.
∠OBY =∠ODX (Alternate interior angles are equal)
∠BOY= ∠DOX (Vertically opposite angles are equal)
ΔBOY ≅ΔDOX (by ASA congruence rule)
OX = OY (Corresponding parts of congruent triangles)
Hence XY is bisected at O.
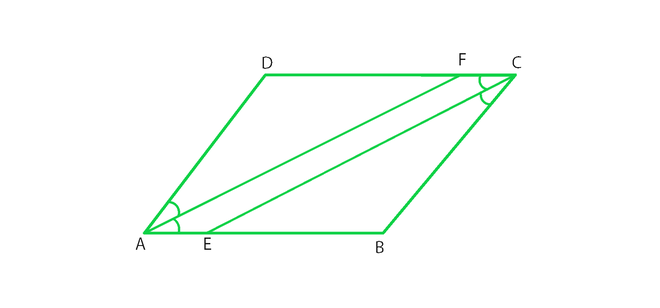
问题26.在图中,ABCD是一个平行四边形,CE对分∠C和AF对分∠A。在以下每种情况下,如果该语句为真,则给出相同的原因:
(i)∠A=∠C
(ii)∠FAB=½∠A
(iii)DCE =½C
(iv)∠CEB=∠FAB
(v)CE∥AF
解决方案:
(i) ∠A = ∠C
True, Since ∠A =∠C = 55° [opposite angles are equal in a parallelogram]
(ii) ∠FAB = ½ ∠A
True, Since AF is the angle bisector of ∠A.
(iii) ∠DCE= ½ ∠C
True, Since CE is the angle bisector of angle ∠C.
(iv) ∠CEB= ∠FAB
True, Since ∠DCE = ∠FAB (opposite angles are equal in a parallelogram).
∠CEB = ∠DCE (alternate angles)
½ ∠C = ½ ∠A [AF and CE are angle bisectors]
(v) CE || AF
True, since one pair of opposite angles are equal, therefore quad. AEFC is a parallelogram.
问题27.平行四边形ABCD的对角线在O. AL和CM处垂直于BD绘制,使得L和M位于BD上。 AL = CM吗?为什么或者为什么不?
解决方案:

Given that,
AL and CM are perpendiculars on diagonal BD.
In ΔAOL and ΔCOM,
∠AOL = ∠COM (vertically opposite angle) ———–(i)
∠ALO = ∠CMO = 90° (each right angle) ——–(ii)
By using angle sum property,
∠AOL + ∠ALO + ∠LAO = 180° ———(iii)
∠COM + ∠CMO + ∠OCM = 180° ———- (iv)
From (iii) and (iv)
∠AOL + ∠ALO + ∠LAO = ∠COM + ∠CMO + ∠OCM
∠LAO = ∠OCM (from (i) and (ii))
In ΔAOL and ΔCOM
∠ALO = ∠CMO (each right angle)
AO = OC (diagonals of a parallelogram bisect each other)
∠LAO = ∠OCM (proved)
therefore, ΔAOL is congruent to ΔCOM
Hence AL = CM (Corresponding parts of congruent triangles)
问题28.点E和F位于平行四边形ABCD的对角线AC上,使得AE =CF。 BFDE是什么类型的四边形?
解决方案:
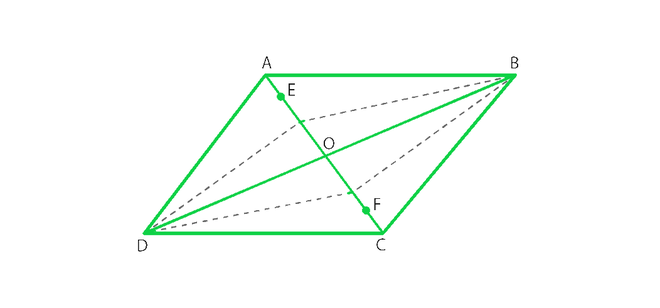
From figure, we conclude that,
In parallelogram ABCD,
AO = OC ———- (i) (Diagonals of a parallelogram bisect each other)
AE = CF ———-(ii) Given
On subtracting (ii) from (i)
AO – AE = OC – CF
EO = OF ——-(iii)
In ΔDOE and ΔBOF,
EO = OF (proved)
DO = OB (Diagonals of a parallelogram bisect each other)
∠DOE = ∠BOF (vertically opposite angles are equal in a parallelogram)
By SAS congruence ΔDOE ≅ ΔBOF
therefore, DE = BF (Corresponding parts of congruent triangles)
In ΔBOE and ΔDOF,
EO = OF (proved)
DO = OB (diagonals of a parallelogram bisect each other)
∠DOF = ∠BOE (vertically opposite angles are equal in a parallelogram)
By SAS congruence ΔDOE ≅ ΔBOF
Hence, DF = BE (Corresponding parts of congruent triangles).
Hence, BFDE is a parallelogram, since one pair of opposite sides are equal and parallel.
问题29.在平行四边形ABCD中,AB = 10厘米,AD = 6厘米。 ∠A的等分线在E,AE和BC处遇到DC,在F处遇到。找到长度CF。
解决方案:
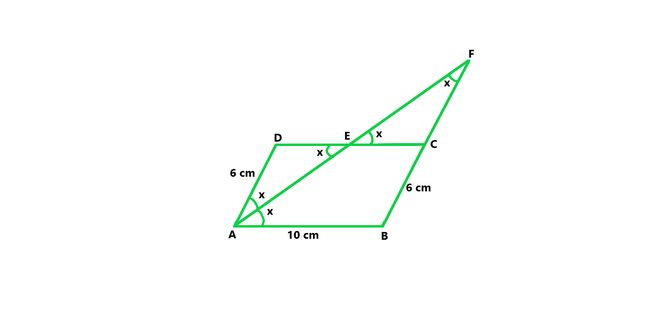
From figure we concluded that,
In a parallelogram ABCD,
Given, AB = 10 cm, AD = 6 cm
CD = AB = 10 cm and AD = BC = 6 cm (In a parallelogram opposite sides are equal)
AE is the bisector of ∠DAE = ∠BAE = x
∠BAE = ∠AED = x (alternate angles are equal)
ΔADE is an isosceles triangle. Since opposite angles in ΔADE are equal.
AD = DE = 6cm (opposite sides are equal)
CD = DE + EC
EC = CD – DE = 10 – 6 = 4cm
∠DEA = ∠CEF = x (vertically opposite angle are equal)
∠EAD = ∠EFC = x (alternate angles are equal)
ΔEFC is an isosceles triangle. Since opposite angles in ΔEFC are equal.
CF = CE = 4cm (opposite side are equal to angles)
Hence CF = 4cm.