八类RD Sharma解法–第17章-了解形状的特殊四边形–练习17.2 |套装2

问题9.菱形的一侧长为4厘米，海拔高度为3.2厘米。画菱形。

解决方案：

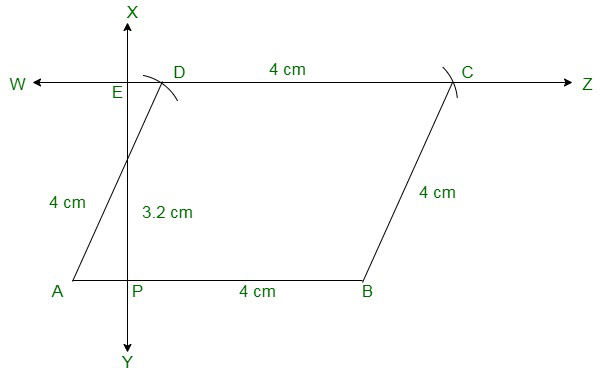
Steps to construct a rhombus:

(i) Draw a line segment of 4 cm

(ii) From point A draw a perpendicular line bisecting the length of 3.2 cm to get point E.

(iii) From point E draw a line parallel to AB.

(iv) From points A and B cut two arcs of length 4 cm on the drawn parallel line to get points D and C.

(v) Join the line segments AD, BC and CD to get rhombus ABCD.

问题10.如果AB = 6 cm，AC = 5 cm，则绘制菱形ABCD。

解决方案：

Steps of construction:

(i) Draw a line segment AB of length 6 cm.

(ii) From point ‘A’ cut an arc of length 5 cm and from point B cut an arc of length 6 cm intersecting at ‘C’.

(iii) Join the line segments AC and BC.

(iv) From point A cut an arc of length 6 cm and from point C cut an arc of 6cm, so that both the arcs intersect at point D.

(v) Join the remaining line segments AD and DC to get rhombus ABCD.

问题11. ABCD是菱形，其对角线在O处相交。

(i)是ΔBOC≅ΔDOC吗?说明使用的一致性条件?

(ii)如果∠BCO=∠DCO，也要声明。

解决方案：

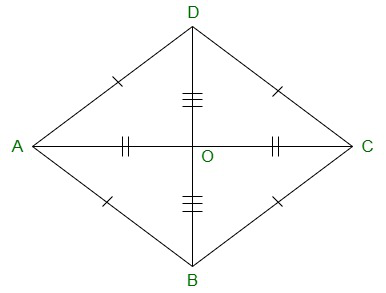
(i) Yes,

In ΔBOC and ΔDOC

Since, in a rhombus diagonals bisect each other, we have,

BO = DO 

CO = CO Common

BC = CD [All sides of a rhombus are equal]

Now,

By using SSS Congruency, ΔBOC≅ΔDOC

(ii) Yes.

Since by,

∠BCO = ∠DCO, by corresponding parts of congruent triangles.

问题12：证明菱形的每个对角线均等其通过的角度。

解决方案：

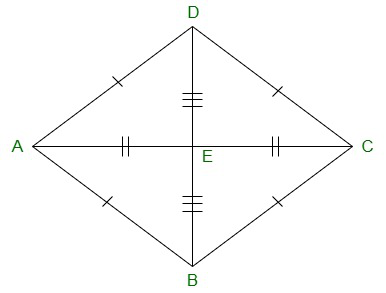
(i) In ΔBOC and ΔDOC

BO = DO [In a rhombus diagonals bisect each other]

CO = CO Common

BC = CD [All sides of a rhombus are equal]

By using SSS Congruency, ΔBOC≅ΔDOC

∠BCO = ∠DCO, by corresponding parts of congruent triangles

Therefore, 

Each diagonal of a rhombus bisect the angle through which it passes.

问题13. ABCD是菱形，其对角线在O处相交。如果AB = 10 cm，对角线BD = 16 cm，则求出对角线AC的长度。

解决方案：

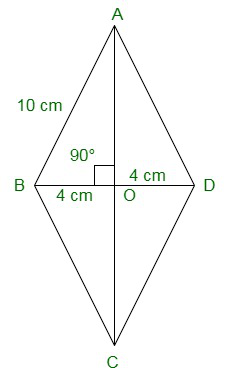
In a rhombus diagonals bisect each other at right angle.

In ΔAOB

BO = BD/2 = 16/2 = 8cm

AB² = AO² + BO² (Pythagoras theorem)

10² = AO² + 8²

100-64 = AO²

AO² = 36

AO = √36 = 6cm

Hence, Length of the diagonal AC is 6 × 2 = 12cm.

问题14.四边形的对角线长度分别为6厘米和8厘米。如果对角线以直角彼此一分为二，那么四边形的每一边的长度是多少?

解决方案：

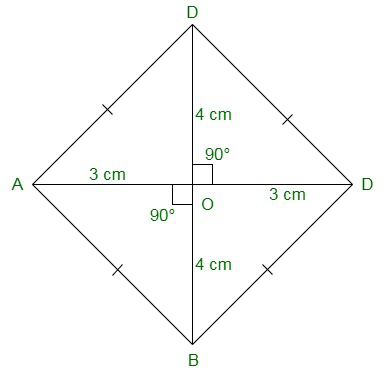
In a rhombus diagonals bisect each other at right angle.

Considering ΔAOB

BO = BD/2 = 6/2 = 3cm

AO = AC/2 = 8/2 = 4cm

Now,

AB² = AO² + BO² (Pythagoras theorem)

AB² = 4² + 3²

AB² = 16 + 9

AB² = 25

AB = √25 = 5cm

Hence, Length of each side of the quadrilateral ABCD is 5cm.