9类NCERT解决方案–第2章多项式–练习2.4

问题1.确定以下哪个多项式具有(x +1)作为因子：

(i)x ³ + x ² + x + 1

解决方案：

p(x) = x³ + x² + x + 1 

Let x+1 be the factor of p(x)
Then x = -1 will be the zero of p(x)
value of p(-1) should be 0
Checking,
=> p(-1) = (-1)³ + (-1)² + (-1) + 1
=> -1 + 1 -1 + 1
=> 0
As p(-1)=0 so (x + 1) is a factor of p(x). 

(ii)x ⁴ + x ³ + x ² + x + 1

解决方案：

p(x) = x⁴+x³+x²+x+1
Let x+1 be the factor of p(x)
Then x = -1 will be the zero of p(x)
value of p(-1) should be 0
Checking,
=> p(-1) = (-1)⁴ + (-1)³ + (-1)² + (-1) + 1
=> – 1 + 1 – 1 + 1 -1
=> -1
=> -1 ≠ 0
As p(-1) ≠ 0 so (x + 1) is not a factor of p(x).

(iii)x ⁴ + 3x ³ + 3x ² + x + 1

解决方案：

p(x) = x⁴+3x³+3x²+x+1  
Let x+1 be the factor of p(x)
Then x = -1 will be the zero of p(x)
value of p(-1) should be 0
Checking,
=> p(-1) = (-1)⁴ + 3(-1)³ + 3(-1)² + (-1) + 1
=> 1 – 3 + 3 – 1 + 1
=> -1
=> -1 ≠ 0
As p(-1) ≠ 0 so (x + 1) is not a factor of p(x).

(iv)x ³ – x ² –(2 +√2)x +√2

解决方案：

p(x) = x³ – x²– (2+√2)x +√2
Let x+1 be the factor of p(x)
Then x = -1 will be the zero of p(x)
value of p(-1) should be 0
Checking,
=> p(-1) = (-1)³ – (-1)²– (2+√2)(-1) +√2
=> -1 – 1 + 2 + √2 + √2
=> 2√2
=> 2√2 ≠ 0
As p(-1) ≠ 0 so (x + 1) is not a factor of p(x).

问题2.在以下每种情况下，使用因子定理确定g(x)是否为p(x)的因子：

(i)p(x)= 2x ³ + x ² –2x-1，g(x)= x + 1

解决方案：

p(x) = 2x³+x²– 2x–1
g(x) = x + 1 
By Factor Theorem we know that if x + 1 is a factor of p(x)
Then value of p(-1) should be 0
Checking,
=> p(-1) = 2(-1)³ + (-1)² – 2(-1) -1
=> -2 + 1 + 2 – 1
=> 0
As p(-1) = 0 therefore (x + 1) is a factor of 2x³ + x² – 2x – 1 

(ii)p(x)= x ³ + 3x ² + 3x + 1，g(x)= x + 2

解决方案：

p(x) = x³+3x²+3x+1 
g(x) = x + 2
By Factor Theorem we know that if x + 2 is a factor of p(x)
Then value of p(-2) should be 0
Checking,
=> p(-2) = (-2)³ + 3(-2)² + 3(-2) +1
=> -8 + 12 – 6 + 1
=> -1
=> -1 ≠ 0
As p(-2) ≠ 0 therefore (x + 2) is not a factor of x³ + 3x² +3x + 1

(iii)p(x)= x ³ – 4x ² + x + 6，g(x)= x – 3

解决方案：

p(x) = x³– 4x²+x+6 
g(x) = x – 3
By Factor Theorem we know that if x – 3 is a factor of p(x)
Then value of p(3) should be 0
Checking,
=> p(3) = (3)³ – 4(3)² + 3 + 6
=> 27 – 36 + 3 + 6
=> 0
As p(3)=0 so (x – 3) is a factor of p(x).

问题3.在以下每种情况下，如果x–1是p(x)的因数，则求出k的值：

(i)p(x)= x ² + x + k

解决方案：

p(x) = x² + x + k 
By Factor Theorem,
As x-1 is a factor of p(x)
then x = 1 is the zero of p(x)
Therefore p(1) = 0
=> p(1) = (1)² + 1 + k
=> 1 + 1 + k = 0
=> 2 + k = 0
=> k = -2

(ii)p(x)= 2x ² + kx +√2

解决方案：

p(x) = 2x² + kx + √2
By Factor Theorem,
As x-1 is a factor of p(x)
then x = 1 is the zero of p(x)
Therefore p(1) = 0
=> p(1) = 2(1)² + k(1) + √2
=> 2 + k + √2 = 0
=> 2 + √2 + k = 0
=> k = – (2 + √2) 

(iii)p(x)= kx ² –√2x + 1

解决方案：

p(x) = kx² – √2x + 1
By Factor Theorem,
As x-1 is a factor of p(x)
then x = 1 is the zero of p(x)
Therefore p(1) = 0
=> p(1) = k(1)² – √2(1) + 1
=> k – √2 + 1 = 0
=> k = √2 – 1

(iv)p(x)= kx ² –3x + k

解决方案：

p(x) = kx² -3x + k
By Factor Theorem,
As x-1 is a factor of p(x)
Then x = 1 is the zero of p(x)
Therefore, p(1) = 0
=> p(1) = k(1)² – 3(1) + k
=> k – 3 + k = 0
=> 2k – 3 = 0
=> k = 3/2

问题4：分解：

(i)12x ² –7x + 1

解决方案：

p(x) = 12x² – 7x + 1
Using splitting the middle term method,
We need to find a pair of numbers whose sum is -7x
and product is 12x²
-7x can be written as the sum of -3x and -4x
12x² can be written as the product of -3x and -4x
=> 12x² – 7x + 1
=> 12x² -3x -4x +1
=> 3x(4x -1) -1(4x -1)
=> (3x – 1)(4x – 1) are the factors of 12x² – 7x + 1

(ii)2x ² + 7x + 3

解决方案：

p(x) = 2x² + 7x + 3
Using splitting the middle term method,
We need to find a pair of numbers whose sum is 7x
and product is 6x²
7x can be written as the sum of 1x and 6x
6x² can be written as the product of 1x and 6x
=> 2x² + 7x + 3
=> 2x² + 1x + 6x + 3
=> 2x(x + 3) + 1(x + 3)
=> (2x + 1)(x + 3) are the factors of 2x² + 7x + 3

(iii)6x ² + 5x-6

解决方案：

p(x) = 6x² + 5x – 6
Using splitting the middle term method,
We need to find a pair of numbers whose sum is 5x
and product is -36x²
5x can be written as the sum of 9x and -4x
-36x² can be written as the product of 9x and -4x
=> 6x² + 5x – 6
=> 6x² + 9x – 4x – 6
=> 3x(2x + 3) – 2(2x + 3)
=> (3x – 2)(2x + 3) are the factors of 6x² + 5x – 6

(iv)3x ² –x–4

解决方案：

p(x) = 3x² – x – 4
Using splitting the middle term method,
We need to find a pair of numbers whose sum is -x
and product is -12x²
-x can be written as the sum of -4x and 3x
-12x² can be written as the product of -4x and 3x
=> 3x² – x – 4
=> 3x² – 4x + 3x – 4
=> 3x(x + 1) – 4(x + 1)
=> (3x – 4)(x + 1) are the factors of 3x² – x – 4

问题5：分解：

(i)x ³ –2x ² –x + 2

解决方案：

p(x) = x³– 2x²– x + 2
Factors of 2 are ±1 and ± 2 
Using Hit and Trial Method
p(1) = (1)³ – 2(1)² – (1) + 2
p(1) = 1 – 2 – 1 + 2
p(1) = 0
Therefore, (x – 1) is a factor of x³ – 2x² – x + 2
Performing Long Division :

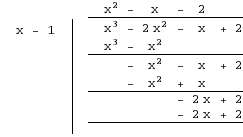
商：x ² – x – 2，余数：0

Dividend = Divisor × Quotient + Remainder
=>p(x) = (x – 1)(x² – x – 2)
=> solving (x² – x -2) 
=> using Splitting the middle term method
=> x² – 2x + x – 2
=> x(x – 2) + 1(x – 2)
=> (x + 1)(x – 2)
=>(x – 1)(x + 1)(x – 2) are the factors of p(x)

(ii)x ³ –3x ² –9x–5

解决方案：

p(x) = x³–3x²–9x–5
Factors of -5 are ±1 and ± 5
Using Hit and Trial Method
let x = 1
p(1) = (1)³ – 3(1)² – 9(1) – 5
p(1) = 1 – 3 – 9 -5
p(1) = -16
p(1) ≠ 0
let x = -1
p(-1) = (-1)³ – 3(-1)² – 9(-1) – 5
p(-1) = -1 – 3 + 9 – 5
p(-1) = -9 + 9
p(-1) = 0
Therefore, (x + 1) is a factor of p(x)
Performing Long Division :

商：x ² – 4x – 5，余数：0

Dividend = Divisor × Quotient + Remainder
=>p(x) = (x + 1)(x² – 4x – 5)
=> solving (x² – 4x – 5)
=> using splitting the middle term method
=> x² -5x + x – 5
=> x(x – 5) + 1(x – 5)
=> (x + 1)(x – 5)
=>(x + 1)(x + 1)(x – 5) are the factors of p(x)

(iii)x ³ + 13x ² + 32x + 20

解决方案：

p(x) = x³+13x²+32x+20
=> Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20
Using Hit and Trial Method
let x = 1
p(1) = (1)³ + 13(1)² + 32(1) + 20
p(1) = 1 + 13 + 32 + 20
p(1) = 66
p(1) ≠ 0
let x = -1
p(-1) = (-1)³ + 13(-1)² + 32(-1) + 20
p(-1) = -1 + 13 – 32 + 20
p(-1) = -33 + 33
p(-1) = 0
Therefore, (x + 1) is a factor of p(x)
Performing Long Division :

商：x ² + 12x + 20，余数：0

Dividend = Divisor × Quotient + Remainder
=> p(x) = (x + 1)(x² + 12x + 20)
=> solving x² + 12x + 20
=> using Splitting the middle term method
=> x² + 10x + 2x + 20
=> x(x + 10) + 2(x + 10)
=> (x + 2)(x + 10) are the factors of x² + 12x + 20
=> (x + 1)(x + 2)(x + 10) are the factors of p(x) 

(iv)2y ³ + y ² –2y-1

解决方案：

p(y) = 2y³+y²–2y–1
=> Factors of -1 are ±1
Using Hit and Trial Method
let x = 1
p(1) = 2(1)³ + (1)² – 2(1) – 1
p(1) = 2 + 1 -2 – 1
p(1) = 0
Therefore, (y – 1) is a factor of p(y)
Performing Long Division :

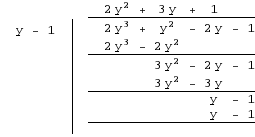
商：2y ² + 3y + 1，余数：0

Dividend = Divisor × Quotient + Remainder
=> p(y) = (y – 1)(2y² + 3y + 1) 
=> solving 2y² + 3y +1
=> using splitting the middle term method
=> 2y² + 2y +y +1
=> 2y(y + 1)+1(2y + 1)
=>(2y + 1)(2y + 1) are the factors of 2y² + 3y + 1
=> (y – 1)(2y + 1)(2y + 1) are the factors of p(y)