问题1:在图中,假设RT = TS,∠1=2∠2和∠4= 2(∠3)。证明ΔRBT≅ΔSAT 。
解决方案:
In the figure,
Given:
RT = TS —-> (equation 1)
∠1 = 2 ∠2 —-> (equation 2)
∠4 = 2 ∠3 —->(equation 3)
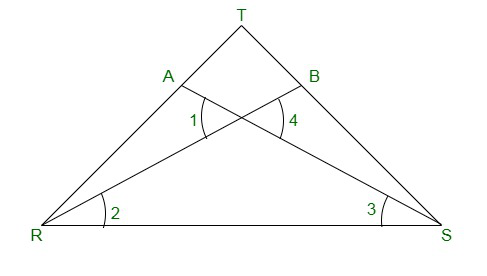
To prove:
ΔRBT ≅ ΔSAT
Let the point of intersection RB and SA be denoted by O
∠AOR = ∠BOS [Vertically opposite angles]
So, ∠1 = ∠4
2 ∠2 = 2 ∠3 [From (equation 2) and (equation 3)]
or
∠2 = ∠3 —->(equation 4)
Now in Δ TRS,
We have RT = TS
Δ TRS is an isosceles triangle
∠TRS = ∠TSR —->(equation 5)
But, ∠TRS = ∠TRB + ∠2 —->(equation 6)
∠TSR = ∠TSA + ∠3 —->(equation 7)
Putting (equation 6) and (equation 7) in (equation 5) we get
∠TRB + ∠2 = ∠TSA + ∠3
∠TRB = ∠TSA [From (equation 6)]
Consider ΔRBT and ΔSAT
RT = ST [From (equation 1)]
∠TRB = ∠TSA [From (equation 6)]
By ASA criterion of congruence, we have
ΔRBT ≅ ΔSAT
问题2:两条直线AB和CD在O处相交,使得BC相等且平行于AD。证明线AB和CD在O处一分为二。
解决方案:
Given:
Lines AB and CD Intersect at O
Such that BC ∥ AD and
BC = AD —->(equation 1)

To prove:
AB and CD bisect at O.
First we have to prove that ΔAOD ≅ ΔBOC
∠OCB =∠ODA {AD||BC and CD is transversal}
AD = BC {from (equation 1)}
∠OBC = ∠OAD {AD||BC and AB is transversal}
By ASA Criterion:
ΔAOD ≅ ΔBOC
OA = OB and OD = OC (By Corresponding parts of congruent triangle )
Therefore,
AB and CD bisect each other at O.
Hence, Proved.
问题3:BD和CE是等腰ΔABC且AB = AC的∠B和∠C的二等分线。证明BD = CE。
解决方案:
Given:
ΔABC is isosceles
Where,
AB = AC
BD and CE are bisectors of ∠ B and ∠ C

To prove:
BD = CE
Since AB = AC (given)
∠ABC = ∠ACB —->(equation 1) {Angles opposite to equal sides are equal}
Since BD and CE are bisectors of ∠ B and ∠ C
∠ABD = ∠DBC =∠ BCE =ECA = ∠B = ∠C —-> (equation 2)
2 2
Now, Consider ΔEBC = ΔDCB
∠EBC = ∠DCB {From (equation 1)}
BC = BC {Common side}
∠BCE = ∠CBD {From (equation 2)}
By ASA congruence criterion,
Δ EBC ≅ Δ DCB
Since corresponding parts of congruent triangles are equal.(c.p.c.t.)
CE = BD
or,
BD = CE
Hence, proved.