9类NCERT解决方案-第1章编号系统-练习1.3

问题1.以十进制形式编写以下内容，并说出每种具有什么样的十进制扩展：

(i)36/100

解决方案：

In the given question, we get

Here, the remainder becomes zero.

Hence, decimal expansion becomes terminating.

36/100 = 0.36

(ii)1/11

解决方案：

In the given question, we get

Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

1/11 = $0.\overline{09}$

(iii) $4\frac{1}{8}$

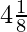
解决方案：

Here, $4\frac{1}{8} = \frac{33}{8}$

In the given question, we get

Here, the remainder becomes zero.

Hence, decimal expansion becomes terminating.

$4\frac{1}{8}$ = 4.125

(iv)3/13

解决方案：

In the given question, we get

Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

3/13 = $0.\overline{230769}$

(v)2/11

解决方案：

In the given question, we get

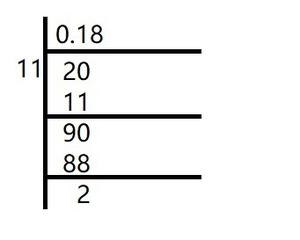
Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

2/11 = $0.\overline{18}$

(vi)329/400

解决方案：

In the given question, we get

Here, the remainder becomes zero.

Hence, decimal expansion becomes terminating.

329/400 = 0.8225

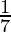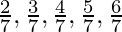问题2。你知道$\frac{1}{7}$ = $0.\overline{142857}$你能预测一下$\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}$是，实际上没有进行长除法?如果是这样，怎么办?

[提示：仔细研究余数，同时仔细寻找1/7的值。]

解决方案：

As it is given,

$\frac{1}{7} = 0.\overline{142857}$

So, 

$\frac{2}{7} = 2(\frac{1}{7}) = 2(0.\overline{142857}) = 0.\overline{285714}$

$\frac{3}{7} = 3(\frac{1}{7}) = 3(0.\overline{142857}) = 0.\overline{428571}$

$\frac{4}{7} = 4(\frac{1}{7}) = 4(0.\overline{142857}) = 0.\overline{571428}$

$\frac{5}{7} = 5(\frac{1}{7}) = 5(0.\overline{142857}) = 0.\overline{714285}$

$\frac{6}{7} = 6(\frac{1}{7}) = 6(0.\overline{142857}) = 0.\overline{857142}$

问题3：以p / q的形式表达以下内容，其中p和q是整数，q≠0。

(一世) 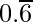$0.\overline{6}$

解决方案：

$0.\overline{6}$= 0.66666……

Lets’s take, x = 0.66666……

10x = 6.666….

So, 

10x – x = (6.6666…..) – (0.66666……..)

9x = 6

x = 6/9 

x = 2/3 

Hence, x is in the form p/q, here p and q are integers and q ≠ 0.

(ii) 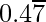$0.4\overline{7}$

解决方案：

$0.4\overline{7}$ = 0.4777777……

Lets’s take, x = 0.4777777……

10x = 4.77777…….

So,

10x – x = (4.77777…….) – (0.4777777……)

9x = 4.3

9x = 43/10 

x = 43/90

Hence, x is in the form p/q, here p and q are integers and q ≠ 0.

(iii) 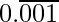$0.\overline{001}$

解决方案：

$0.\overline{001}$ = 0.001001001……

Lets’s take, x = 0.001001001……

1000x = 1.001001001……

So,

1000x – x = (1.001001001……) – (0.001001001……)

999x = 1

x = 1/999

Hence, x is in the form p/q, here p and q are integers and q ≠ 0.

问题4.快递0.99999…。以p / q的形式，您对答案感到惊讶吗?与您的老师和同学讨论答案为什么有意义。

解决方案：

Lets’s take, x = 0.99999……

10x = 9.99999….

So,

10x – x = (9.99999…..) – (0.99999……..)

9x = 9

x = 1

As, 0.9999….. just goes on, then at some point of time there is no gap between 1 and 0.9999….

We can observe that, 0.999 is too much near 1, hence, 1 is justified as the answer.

Hence, x is in the form p/q, where p and q are integers and q ≠ 0.

问题5.在小数扩展为1/17的重复数字块中，最大位数是多少?执行除法以检查您的答案。

解决方案：

In the given question,

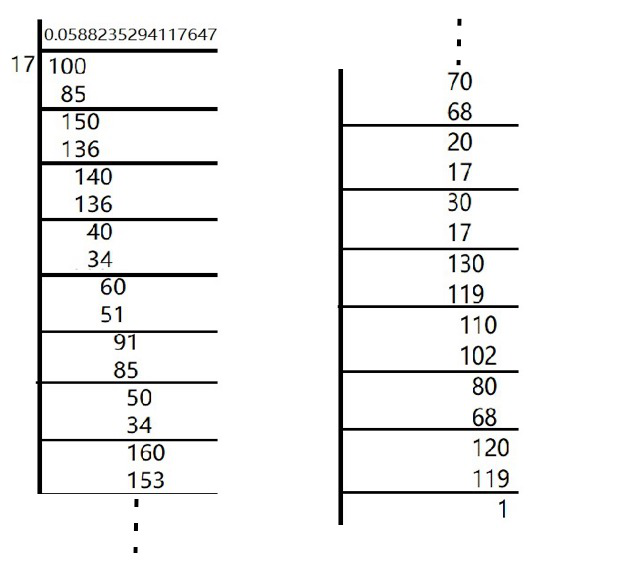
There are 16 digits in the repeating block of the decimal expansion of 1/17

Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

1/17 = $0.\overline{0588235294117647}$

问题6。看一下p / q(q≠0)形式的有理数示例，其中p和q是整数，除1外没有其他公因子，并且以小数点表示(扩展)。你能猜出q必须满足什么性质吗?

解决方案：

We observe that when q is 2, 4, 5, 8, 10… Then the decimal expansion is terminating. 

Let’s take some example,

1/2 = 0. 5, denominator q = 2¹

7/8 = 0. 875, denominator q =2³

4/5 = 0. 8, denominator q = 5¹

So, we conclude that terminating decimal may be obtained in the situation where 

prime factorization of the denominator of the given fractions has the power 

of only 2 or only 5 or both.

In the form of 2^m × 5ⁿ, where n, m are natural numbers.

问题7.写出三个数字，它们的十进制扩展为非终止性非重复性。

解决方案：

As we know that all irrational numbers are non-terminating non-recurring. 

So,

√5 = 2.23606798…….

√27 =5.19615242……

√41 = 6.40312424…..

问题8：在有理数5/7和9/11之间找到三个不同的无理数。

解决方案：

As, decimal expansion of

5/7 = $0.\overline{714285}$

9/11 = $0.\overline{81}$

Hence, three different irrational numbers between them can be as follows,

0.73073007300073000073…

0.75075007300075000075…

0.76076007600076000076…

问题9.将以下数字分类为有理数或无理数：

(i)√23

解决方案：

√23 = 4.79583152……

As the number is non-terminating non-recurring.

It is an irrational number.

(ii)√225

解决方案：

√225 = 15 = 15/1 

As the number can be represented in p/q form, where q ≠ 0.

It is a rational number.

(iii)0.3796

解决方案：

As, the number 0.3796, is terminating.

It is a rational number.

(iv)7.478478…

解决方案：

As, the number 7.478478, is non-terminating but recurring.

It is a rational number.

(v)1.101001000100001…

解决方案：

As, the number 1.101001000100001…, is non-terminating but recurring.

It is a rational number.