9类RD Sharma解决方案–第14章四边形-练习14.4 |套装1

问题1.在ΔABC中，D，E和F分别是BC，CA和AB的中点。如果侧面AB，BC和CA的长度分别为7cm，8 cm和9 cm，请找到ΔDEF的周长。

解决方案：

From the question it is given that

AB = 7 cm, BC = 8 cm, AC = 9 cm

Find: the perimeter of ΔDEF

In ∆ABC,

D, E and F are the mid points of BC, CA and AB.

So, by midpoint theorem

 EF = 1/2 BC,                                      

 DF = 1/2 AC and DE = 1/2 AB             

Now, we find the perimeter of ΔDEF

So, Perimeter of ∆DEF = DE + EF + DF

= (1/2) AB + (1/2) BC + (1/2) AC

= 1/2 (AB + BC + AC)  

= 1/2(7 + 8 + 9)

= 1/2 (24)

= 12 cm

Hence, the perimeter of ΔDEF is 12 cm

问题2：在ΔABC中，∠A= 50°，∠B= 60°，∠C= 70°。找到通过连接三角形三角形各边的中点而形成的三角形角度的度量。

解决方案：

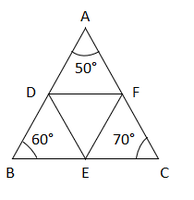
From the question it is given that

∠A = 50°, ∠B = 60° and ∠C = 70°

In ΔABC,

D, E, and F are mid points of AB, BC, and AC

So from Midpoint Theorem

DE ∥ AC, DE = (1/2) AC          

DE = (1/2) AC = CF                

In Quadrilateral DECF

DE ∥ AC, DE = CF [Proved above]                

Hence, DECF is a parallelogram.

So, ∠C = ∠D = 70°  [Because the opposite sides of a parallelogram are equal]

Similarly,

BEFD is a parallelogram, 

So, ∠B = ∠F = 60°

ADEF is a parallelogram, 

So, ∠A = ∠E = 50°

Hence, the angles of ΔDEF are

∠D = 70°, ∠E = 50°, ∠F = 60°

问题3.在三角形中，P，Q和R分别是边BC，CA和AB的中点。如果AC = 21厘米，BC = 29厘米，AB = 30厘米，请找到四边形ARPQ的周长。

解决方案：

From the question it is given that

AC = 21cm, BC = 29 cm and AB = 30 cm

In ΔABC,

R and P are mid points of AB and BC

So from Midpoint Theorem

RP ∥ AC, RP = (1/2) AC                             

In quadrilateral ARPQ,

RP ∥ AQ, RP = AQ [Because the opposite sides of a parallelogram 

                                 are equal and parallel to each other]

Hence, AQPR is a parallelogram

Now,

 AR = (1/2) AB = 1/2 x 30 = 15 cm

So, AR = QP = 15 cm [Because the opposite sides of a parallelogram are equal]

Similarly,

 RP = (1/2) AC =1/2 x 21 = 10.5 cm

So, RP = AQ = 10.5 cm [Because the opposite sides of a parallelogram are equal]

Now we find the perimeter of the quadrilateral ARPQ

So, Perimeter of ARPQ = AR + QP + RP + AQ

= 15 + 15 + 10.5 + 10.5

= 51 cm

Hence, the perimeter of the ARPQ = 51cm

问题4：在ΔABC中，将中位数AD生成为x，使得AD = DX。证明ABXC是平行四边形。

解决方案：

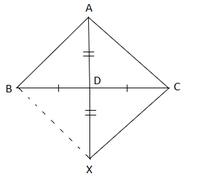
From the question it is given that

AD = DX 

BD = DC 

To prove: Prove that ABXC is a parallelogram.

Proof: Now,

In a quadrilateral ABXC, we have

AD = DX               [Given]

BD = DC               [Given]

So, diagonals AX and BC bisect each other.

Hence, ABXC is a parallelogram         

问题5.在ΔABC中，E和F分别是AC和AB的中点。 AP到BC的海拔高度在Q处与FE相交。证明AQ = QP。

解决方案：

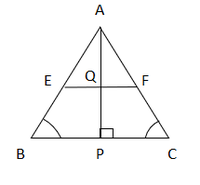
In ΔABC

E and F are mid points of AB and AC

So from midpoint theorem

EF ∥ FE, (1/2) BC = FE                 

Similarly,

In ΔABP

F is the mid-point of AB 

So, from mid-point theorem

So, FQ ∥ BP [since EF ∥ BP]

Q is the mid-point of AP            

Hence AQ = QP

问题6.在ΔABC中，BM和CN分别垂直于B和C在通过A的任何直线上。如果L是BC的中点，则证明ML = NL。

解决方案：

In ΔBLM and ΔCLN

∠BML = ∠CNL = 90°

BL = CL         [Because L is the mid-point of BC]

∠MLB = ∠NLC      [Because vertically opposite angle]

So, ΔBLM ≅ ΔCLN

Hence, by corresponding parts of congruent triangles

LM = LN

问题7。在图中，三角形ABC是在B处的直角三角形。假设AB = 9 cm，AC = 15 cm，而D，E分别是AB和AC边的中点，则计算

(i)公元前的长度

(ii)ΔADE的面积。

解决方案：

From the question it is given that

AB = 9 cm, AC = 15 cm, ∠B = 90°

 D, E are the mid-points of AB and AC

In ΔABC,

Using Pythagoras theorem

AC² = AB² + BC²                                         

= 152 = 92 + BC²

= BC² = 225 – 81 = 144

 BC = 12

Similarly,

AD = DB = AB/2 = 9/2 = 4.5 cm     [D is the mid−point of AB]

D and E are mid-points of AB and AC

So, from mid-point theorem

DE ∥ BC ⇒ DE = BC/2                                      

Now, we find the area of ΔADE 

So, Area = 1/2 x AD x DE

= 1/2 x 4.5 x 6

= 13.5

Hence, the area of ΔADE is 13.5 cm²

问题8.在图中，M，N和P分别是AB，AC和BC的中点。如果MN = 3厘米，NP = 3.5厘米，MP = 2.5厘米，则计算BC，AB和AC。

解决方案：

From the question it is given that

MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm.

Find: the value of BC, AB and AC

In ΔABC

M and N are mid-points of AB and AC

So, from mid-point theorem

MN = (1/2) BC, MN ∥ BC               

= 3 = (1/2) BC

= 3 x 2 = BC

= BC = 6 cm

Similarly,

AC = 2MP = 2 (2.5) = 5 cm

AB = 2 NP = 2 (3.5) = 7 cm

Hence, values of BC, AB, and AC are 6 cm,7 cm, and 5 cm

问题9. ABC是一个三角形，并且通过A，B，C线分别平行于BC，CA和AB绘制，分别与P，Q和R相交。证明ΔPQR的周长是ΔABC的周长的两倍。

解决方案：

To prove: Perimeter of ΔPQR is double the perimeter of ΔABC.

Proof: 

In ΔABC

It is given that the ΔABC pass through A, B, C lines are drawn 

parallel to BC, CA and AB and intersecting at P, Q and R.

So, ABCQ and ARBC are parallelograms.

BC = AQ and BC = AR          [ Because the opposite sides of a parallelogram are equal]

= AQ = AR

= A is the mid-point of QR

Now we know that,

 B and C are the mid points of PR and PQ 

So, from mid-point theorem

AB = (1/2) PQ, BC = (1/2) QR, CA = (1/2) PR     

= PQ = 2AB, QR = 2BC and PR = 2CA

= PQ + QR + RP = 2 (AB + BC + CA)

Perimeter of ΔPQR = 2 (perimeter of ΔABC)

Hence proved.

问题10.在图中，BE⊥AC，AD是从A到BC与BE在H中相交的任意线。P，Q和R分别是AH，AB和BC的中点。证明∠PQR= 90°

解决方案：

From the question it is given that

BE ⊥ AC and P, Q and R are the mid-point of AH, AB and BC.

To prove: ∠PQR = 90°

Proof: 

In ΔABC, 

Q and R are mid-points of AB and BC 

So, from mid-point theorem

QR ∥ AC     ….. (i)          

In ΔABH, 

Q and P are the mid-points of AB and AH 

So, from mid-point theorem

QP ∥ BH   ….. (ii)          

But, BE⊥AC

So, from eq(i) and (ii) we have,

QP⊥QR

∠PQR = 90°

Hence Proved