问题1.在平行四边形ABCD中,确定角度C和D之和。
解决方案:

In the given ||gm ABCD,
∠C + ∠D = 180°
Because∠C and ∠D are consecutive interior angles on the same side of CD traversal, so their sum is equal to 180°.
问题2.在平行四边形ABCD中,如果∠B= 135°,则确定其其他角度的大小。
解决方案:
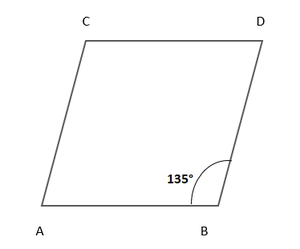
In the given ||gm ABCD,
∠B = 135°
So ∠D = ∠B = 135° (Because opposite angles of a ABCD ||gm)
But ∠A + ∠B = 180° (Sum of consecutive angles) ….(i)
Now put the value of ∠B in eq(i)
∠B + 135° = 180°
∠A = 180° – 135° = 45°
But ∠C = ∠B = 45° (Opposite angles of a ||gm)
Here, the other angles are ∠A = 45°, ∠C = 45°, and ∠D = 135°.
问题3. ABCD是一个正方形,AC和BD在O处相交。表示∠AOB的量度。
解决方案:

In the given square ABCD,
Given that diagonal AC and BD intersect each other at O
Hence, ∠AOB = 90°, because in square diagonals are bisect each other at right angle.
问题4. ABCD是一个withABD = 40°的矩形。确定∠DBC。
解决方案:

In rectangle ABCD,
Given that ∠ABD = 40°, ∠B = 90°, BD is its diagonal
∠ABD + ∠DBC = 90° ……….(i)
Put the value of∠ABD = 40° in eq(i)
⇒ 40° + ∠DBC = 90°
⇒ ∠DBC = 90° – 40° = 50°
Hence, the value of angle ∠DBC = 50°
问题5.平行四边形ABCD的边AB和CD在E和F处一分为二。证明EBFD是平行四边形。
解决方案:
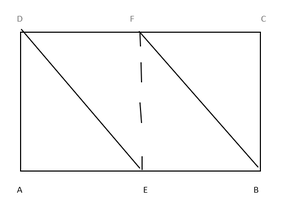
In the given ||gm ABCD,
Given that E and F are the mid points of the line AB and CD
and DE and BF are joined
To prove: EBFD is a ||gm
Construction: Join EF
Proof: ABCD is a ||gm
So, AB = CD and AB || CD (Opposite sides of a ||gm are equal and parallel to each other)
EB || DF and EB = DF (Given that E and F are mid points of AB and CD)
Hence, proved EBFD is a ||gm.
问题6. P和Q是平行四边形ABCD的对角线BD的三等分点。证明CQ与AP平行。还要证明AC将PQ对等。
解决方案:

In the given ||gm ABCD
It is given that P and Q are the points of trisection of the diagonal BD
To prove: (i) CQ || AP
(ii)AC bisects PQ
Proof: As we know that the diagonals of a parallelogram bisect each other
So, AO = OC and BO = OD
According to figure P and Q are point of trisection of BD
So BP = PQ = QD …(i)
BO = OD and BP = QD …(ii)
Now subtract, eq(ii) from eq(i) we get
OB – BP = OD – QD
⇒ OP = OQ
In quadrilateral APCQ,
OA = OC and OP = OQ (proved above)
Diagonals AC and PQ bisect each other at O
So, APCQ is a parallelogram
Hence, AP || CQ
问题7. ABCD是一个正方形。 E,F,G和H分别是AB,BC,CD和DA上的点,因此AE = BF = CG = DH。证明EFGH是正方形。
解决方案:

In the given square ABCD
It is given that E, F, G and H are the points on AB, BC, CD and DA respectively
Such that AE = BF = CG = DH
To prove : EFGH is a square
Proof : It is given that E, F, G and H are points on the sides AB, BC, CA and DA respectively such that
AE = BF = CG = DH = x (suppose)
Then BE = CF = DG = AH = y (suppose)
Now in ∆AEH and ∆BFE
AE = BF (given)
∠A = ∠B (each 90°)
AH = BE (proved)
Hence, by SAS criterion
∆AEH ≅ ∆BFE
∴ ∠1 = ∠2 and ∠3 = ∠4 (C.P.C.T.)
But ∠1 + ∠3 = 90° and ∠2 + ∠4 = 90° (∠A = ∠B = 90°)
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 90° + 90° = 180°
⇒ ∠1 + ∠4 + ∠1 + ∠4 = 180°
⇒ 2(∠1 + ∠4) = 180°
⇒ ∠1 + ∠4 = 180°/2 = 90°
∴ ∠HEF = 180° – 90° = 90°
Similarly, we can prove that
∠F = ∠G = ∠H = 90°
Since sides of the EFGH is are equal and each angle is of 90°
Hence, EFGH is a square.
问题8. ABCD是菱形,EABF是一条直线,使得EA = AB = BF。证明生产时的ED和FC成直角相交。
解决方案:

Given that ABCD is a rhombus
EABF is a straight line such that
EA = AB = BF
Now join ED and FC
Which meet at point G
To prove: ∠EGF = 90°
Proof: As we know that the diagonals of a rhombus bisect
each other at right angles
AO = OC, BO = OD
So, ∠AOD = ∠COD = 90°
and ∠AOB = ∠BOC = 90°
In ∆BDE,
A and O are the mid-points of BE and BD respectively.
AO || ED
Similarly, OC || DG
In ∆ CFA, B and O are the mid-points of AF and AC respectively
OB || CF and OD || GC
Now in DOCG
OC || DG and OD || CG
Hence, DOCG is a parallelogram.
∠DGC = ∠DOC (Opposite angles of ||gm are equal)
∠DGC = 90° (because∠DOC = 90°)
Hence, proved
问题9. ABCD是一个平行四边形,AD生成为E,因此DE = DC = AD,并且生成的EC满足F中生成的AB。证明BF = BC。
解决方案:
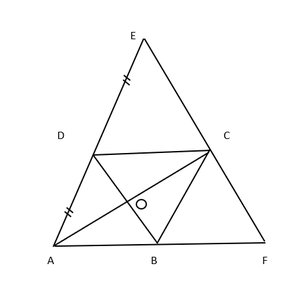
In the given ||gm ABCD,
AB is produced to E so
DE = DC = AD
Also EC produced meets AB produced in F.
To prove : BF = BC
Proof: In ∆ACE,
O and D are the mid points of sides AC and AE
DO || EC and DB || FC
⇒ BD || EF
AB = BF
But AB = DC (Opposite sides of ||gm are equal)
DC = BF
Now in ∆EDC and ∆CBF,
DC = BF (proved)
∠EDC = ∠CBF
(because ∠EDC = ∠DAB corresponding angles)
∠DAB = ∠CBF (corresponding angles)
∠ECD = ∠CFB (corresponding angles)
So, by ASA criterion,
∆EDC ≅ ∆CBF
DE = BC (By C.P.C.T.)
⇒ DC = BC
⇒ AB = BC
⇒ BF = BC (∵ AB = BF proved)
Hence, proved