问题11。在图中,AB = AC和CP∥BA和AP是∆ABC的外部∠CAD的平分线。证明
(i)∠PAC=∠BCA。
(ii)ABCP是平行四边形。

解决方案:
From the question it is given that
AB = AC, CD ∥ BA and AP is the bisector of exterior ∠CAD of ΔABC
(i) So, we have
AB = AC [Given]
∠ACB = ∠ABC [Because opposite angles of equal sides of triangle are equal]
Now, ∠CAD = ∠ABC + ∠ACB
= ∠PAC + ∠PAD = 2∠ACB [∠PAC = ∠PAD]
= 2∠PAC = 2∠ACB
=∠PAC = ∠ACB
Hence proved
(ii) Now, we have
∠PAC = ∠BCA [Proved above]
AP ∥ BC and CP ∥ BA [Given]
Hence, ABCP is a parallelogram.
问题12. ABCD是一种风筝,AB = AD,BC = CD。证明通过将边的中点依次连接而找到的图形是矩形。
解决方案:

From the question it is given that
A kite ABCD having AB = AD and BC = CD.
Join PQ, QR, RS and SP
So, P, Q, R, S are the mid-points of sides AB, BC, CD and DA.
Now e have to prove that PQRS is a rectangle.
Proof:
In ∆ABC,
It is given that P and Q are the mid-points of AB and BC
So from mid point theorem
PQ ∥ AC and PQ = (1/2) AC …. (i)
In ∆ADC,
It is given that R and S are the mid-points of CD and AD
So from mid point theorem
RS ∥ AC and RS = (1/2) AC …. (ii)
From eq(i) and (ii) we have
PQ ∥ RS and PQ = RS
So, PQRS is a parallelogram.
Now, we prove that in parallelogram PQRS on angle is a right angle.
Since AB = AD
= 12AB = 12AD
= AP = AS … (iii)
= ∠1 = ∠2 …. (iv)
Now, in ΔPBQ and ΔSDR, we have
PB = SD [AD = AB ⇒ (1/2) AD = (1/2) AB]
BQ = DR [Since PB = SD]
And PQ = SR [Since, PQRS is a parallelogram]
So, by SSS criterion of congruence, we have
ΔPBQ ≅ ΔSDR
By c.p.c.t
= ∠3 = ∠4
Now, ∠3 + ∠SPQ + ∠2 = 180°
And ∠1 + ∠PSR + ∠4 = 180°
∠3 + ∠SPQ + ∠2 = ∠1 + ∠PSR + ∠4
= ∠SPQ = ∠PSR [∠1 = ∠2 and ∠3 = ∠4]
From the figure we know that transversal PS cuts parallel lines SR and PQ at S and P
So, ∠SPQ + ∠PSR = 180°
= 2∠SPQ = 180°
= ∠SPQ = 90° [∠PSR = ∠SPQ]
Hence, PQRS is a parallelogram and∠SPQ = 90°.
问题13.设ABC为等腰三角形,其中AB = AC。如果D,E,F分别是BC,CA和AB边的中点,则表明线段AD和EF彼此成直角二等分。
解决方案:

To prove : segment AD and EF bisect each other at right angles.
Proof:
In ΔABC,
It is given that D, E and F are mid-points of sides BC, CA and AB
So from mid point theorem
AB ∥ DE and AC ∥ DF
AF ∥ DE and AE ∥ DF
ABDE is a parallelogram.
AF = DE and AE = DF [Because opposite sides of parallelogram are congruent]
So from mid point theorem
(1/2) AB = DE and (1/2) AC = DF
DE = DF
AE = AF = DE = DF
ABDF is a rhombus.
AD and FE bisect each other at right angle.
Hence Proved
问题14. ABC是一个三角形。 D是AB上的一点,使得AD =(1/4)AC,E是AC上的一点,从而AE =(1/4)AC。证明DE =(1/4)BC。
解决方案:

To prove : DE = (1/4) BC.
Proof:
In ΔABC,
D is a point on AB so,
AD = (1/4)
AB and E is a point on AC so,
AE = (1/4) AC.
Let us assume P and Q be the mid-points of AB and AC
Then PQ ∥ BC
So from mid point theorem
PQ = (1/2) BC …. (i)
In ΔAPQ,
D and E are the mid-points of AP and AQ
So from mid point theorem
(1/2) DE ∥ PQ, and DE = (1/2) PQ …. (ii)
From eq(i) and (ii) we know that,
DE = (1/2) PQ = (1/2) ((1/2) BC)
DE = (1/2) BC
Hence proved.
问题15.在图中,ABCD是一个平行四边形,其中P是DC的中点,Q是AC上的一个点,使得CQ =(1/2)AC。如果产生的PQ在R处遇到BC,则证明R是BC的中点。
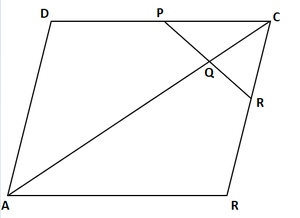
解决方案:
Now join B and D.
Suppose AC and BD intersect at O.
So from mid point theorem
Then OC = (1/2) AC
Now,
CQ = (1/4) AC
⇒ CQ = 1/2((1/2) AC)
= (1/2) OC
In ΔDCO,
PQ ∥ DO [Because P and Q are mid points of DC and OC]
Similarly in ΔCOB,
QR ∥ OB [Because Q is the mid-point of OC]
R is the mid-point of BC.
Hence Proved
问题16。在图中,ABCD和PQRC是矩形,Q是AC的中点。证明
(i)DP = PC
(ii)PR =(1/2)AC
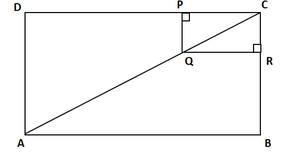
解决方案:
(i) In ΔADC,
It is given that Q is the mid-point of AC such that PQ ∥ AD
So, P is the mid-point of DC.
From mid point theorem
DP = DC
Hence Proved
(ii) Similarly,
PR = (1/2) BD [R is the mid-point of BC]
PR = (1/2) AC [Diagonal of rectangle are equal, BD = AC]
Hence Proved
问题17:ABCD是一个平行四边形。 E和f分别是AB和CD的中点。 GH是分别在G,P和H处与AD,EF和BC相交的任何线。证明GP = PH。
解决方案:

From the question it is given that
ABCD is a parallelogram
E and F are mid-points of AB and CD
AE = BE = (1/2) AB
And CF = DF = (1/2) CD
But, AB = CD
(1/2)AB = (1/2) CD
BE = CF
Also, BE ∥ CF [∴ AB ∥ CD]
Hence, BEFC is a parallelogram
BC ∥ EF and BE = PH …. (i)
Now, BC ∥ EF
AD ∥ EF [BC ∥ AD]
Hence, AEFD is a parallelogram.
AE = GP
So, AE = BF [E is the mid-point of AB]
GP = PH.
Hence Proved.
问题18:BM和CN垂直于穿过三角形ABC的顶点A的线。如果L是BC的中点,则证明LM = LN。
解决方案:
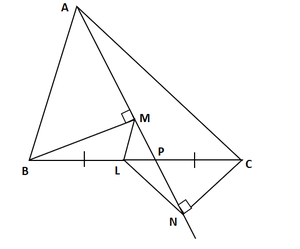
To prove: LM = LN
Draw LS perpendicular to line MN.
The lines BM, LS and CN are perpendicular on MN line and parallel to each other.
According to Intercept Theorem,
From above figure we know that, MB, LS and NC are three parallel
lines and the two transversal lines are MN and BC.
BL = LC [L is mid-point of BC]
We know that,
MS = SN ….. (i) [By Intercept Theorem]
Now, In ΔMLS and ΔLSN
MS = SN [From equation (i)]
∠LSM = ∠LSN = 90° LS ⊥ MN]
And SL = LS [common side]
By SAS Congruency Rule
ΔMLS ≅ ΔLSN
Hence, by c.p.c.t
LM = LN
Hence Proved
问题19:证明,连接四边形二等分的对边的中点的线段彼此相等。
解决方案:

Let us considered ABCD is a quadrilateral in which
P, Q, R and S are mid-points of sides AB, BC, CD and DA
Now, join PQ, QR, RS, SP, and BD
In ΔABD,
It is given that P and S are mid-points of sides AB and DA
So from mid point theorem
SP ∥ BD and SP = (1/2) BD …. (i)
In ΔBCD
It is given that Q and R are mid-points of sides BC and CD
So from mid point theorem
QR ∥ BD and QR = (1/2) BD …. (ii)
Now,
From eq(i) and (ii)
SP ∥ QR and SP = QR
So, SPQR is a parallelogram [ Diagonals of a parallelogram bisect each other]
Hence Proved, PR and QS bisect each other.
问题20.填空以使以下陈述正确:
(i)通过连接等腰三角形边的中点而形成的三角形是____________。
(ii)通过连接直角三角形的边的中点而形成的三角形是____________。
(iii)通过连接四边形的连续边的中点而形成的数字是____________。
解决方案:
(i) Isosceles
(ii) Right triangle
(iii) Parallelogram