10类RD Sharma解决方案–第14章坐标几何–练习14.2 |套装2

问题20.平行四边形的三个顶点是(3，4)，(3，8)和(9，8)。找到第四个顶点。

解决方案：

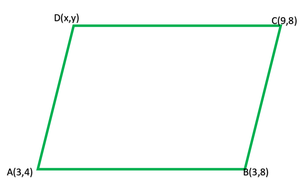
Let ABCD be a parallelogram and vertices will be A (3, 4), B (3, 8), C (9, 8)

and the co-ordinates of fourth vertex D be(x, y)

Now AB = 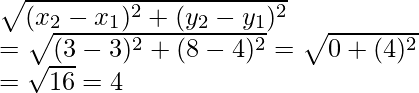$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(3-3)^2+(8-4)^2}=\sqrt{0+(4)^2}\\ =\sqrt{16}=4$

Similarly, BC = 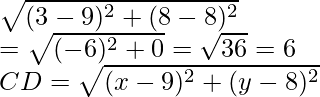$\sqrt{(3-9)^2+(8-8)^2}\\ =\sqrt{(-6)^2+0}=\sqrt{36}=6\\ CD=\sqrt{(x-9)^2+(y-8)^2}$

and DA = $\sqrt{(3-x)^2+(4-y)^2}$

Hence, ABCD is a ||gm

Here, AB = CD and BC = AD

CD = $\sqrt{(x-9)^2+(y-8)^2}=4$

On squaring both sides we get

(x – 9)² + (y – 8)² = (4)²

x² – 18x + 81 + y² – 16y + 64 = 16

x² + y² – 18x – 16y = 16 – 81 – 64

x² + y² – 18x – 16y = -129    ………..(i)

Similarly, AD = $\sqrt{(3-x)^2+(4-y)^2}=6$

On squaring both sides we get

(3 – x)² + (4 – y)² = 26                 

9 + x² – 6x + 16 + y² – 8y = 36

x² + y² – 6x – 8y = 36 – 9 – 16

x² + y² – 6x – 8y = 11    ………..(ii)

Now on subtracting eq(i) from (ii), we get

12x + 8y = 140

3x + 2y = 35

2y = 35 – 3x

y = (35 – 3x)/2    ………..(iii)

Now substituting the value of y in eq (ii)

$x^2(\frac{35-3x}{2})^2-6x-8(\frac{35-3x}{2})=11\\ x+\frac{1225+9x^2-210x}{4}-6x-140+12x=11$

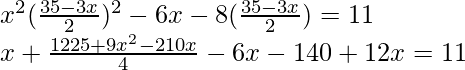
4x² + 1225 + 9x² – 210x – 24x – 560 = 44

13x² – 186 + 621 = 0

13x² – 117x – 69x + 621 = 0

13x(x – 9) – 69(x – 9) = 0

(x – 9)(13x – 69) = 0

Either x – 9 = 0, then x = 9

 or 13x – 69 = 0, then x69/13 which is not possible

So, x = 9

Hence, the vertex will be (9,4)

问题21：找到一个与点A(-5，4)和点B(-1，6)等距的点。有多少这样的点?

解决方案：

Let us considered P (h, k) be the point which is equidistant from the points A (-5, 4) and B (-1, 6).

So, PA = PB

Therefore, (PA)² = (PB)²

Now by distance formula, we get

(-5 – h)² + (4 – k)² = (-1 – h)² + (6 – k)²

25 + h² + 10h + 16 + k² – 8k = 1h² + 2h + 36 + k² – 12k

25 + 10h + 16 – 8k = 1 + 2h + 36 – 12k

8h + 4k + 41 – 37 = 0

8h + 4k + 4 = 0

2h + k + 1 = 0          …….(i)

Midpoint of AB = ((-5 – 1)/2, (4 + 6)/2) = (-3, 5) 

At point (-3, 5), from eq(i)

2h + k = 2(-3) + 6

-6 + 5 = -1

2h + k + 1 = 0

So, the mid-point of AB satisfy the Eq. (i).

Hence, infinite number of points, in fact all points which are solution 

of the equation 2h + k + 1 = 0, are equidistant from the point A and B.

Replacing h, k, by x, y in above equation, we have 2x + y + 1 = 0

问题22.圆的中心是(2a，a – 7)。如果圆通过点(11，-9)且直径为10√2单位，则找到a的值。

解决方案：

According to the question

Distance between the centre C (2a, a – 1) and the point P (11, -9), which lie on the circle = Radius of circle

So, Radius of circle = $\sqrt{(11-2a)^2+(-9-a+7)^2}$      …..(i)

Given that, length of diameter = 10√2

Therefore, length of radius = Length of diameter/2

= 10√2/2 = 5√2

Now put this value in eq(i), we get

$5\sqrt{2}=\sqrt{(11-2a)^2+(-2-a)^2}$

Squaring on both sides, we get

50 = (11 – 2a)² + (2 + a)²

50 = 121 + 4a² – 44a + 4 + a² + 4a

5a² – 40a + 75 = 0

a² – 8a + 15 = 0

a² – 5a – 3a + 15 = 0

a(a – 5) – 3(a – 5) = 0

(a – 5)(a – 3) = 0

So, a = 3, 5

Hence, the required values of a are 5 and 3.

问题23。阿尤什开始从他的房子走到办公室。他没有直接去办公室，而是先去了一家银行，从那里到女儿的学校，然后到达了办公室。 Ayush到达办公室要多走多少距离? (假设所覆盖的所有距离均为直线)。如果房屋位于(2，4)，银行位于(5，8)，学校位于(13，14)，办公室位于(13，26)，则坐标以公里为单位。

解决方案：

Accordin to the figure

Distance between two points $d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Now, distance between house and bank

$=\sqrt{(5-2)^2+(8-4)^2}\\ =5$

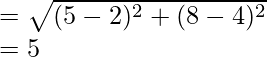
Distance between bank and daughter’s 

School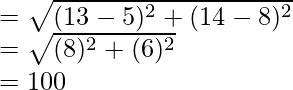$=\sqrt{(13-5)^2+(14-8)^2}\\ =\sqrt{(8)^2+(6)^2}\\ =100$

Distance between daughter’s school and office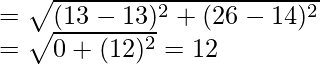$=\sqrt{(13-13)^2+(26-14)^2}\\ =\sqrt{0+(12)^2}=12$

Total distance (house+bank+school+office) travelled = 5 + 10 + 12 = 27 units

Distance between house to offices

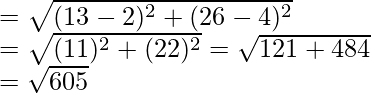$=\sqrt{(13-2)^2+(26-4)^2}\\ =\sqrt{(11)^2+(22)^2}=\sqrt{121+484}\\ =\sqrt{605}$ = 24.59 = 24.6km

So, the extra distance travelled by Ayush in reaching his office = 27 – 24.6 = 2.4km. 

Hence, the required extra distance travelled by Ayush is 2.4 km

问题24.如果点P(0，2)与(3，k)和(k，5)等距，则求k的值。

解决方案：

Let us considered P (0, 2) is equidistant from A (3, k) and B (k, 5)

PA = PB

=> PA² = PB²

$=\sqrt{(0-3)^2+(2-k)^2}$

Therefore, PA² = (0 – 3)² + (2 – k)²

= (-3)² + (2 – k)²

= k² – 4k + 13

Similarly, PB² = (k – 0)² + (5 – 2)²

= k² + (3)² = k² + 9

Therefore, PA = PB

PA² = PB²

k² – 4k + 13 = k² + 9

-4k = 9 – 13

-4k = -4

k = -4/-4 = 1

Hence, K = 1.

问题25.如果(-4，3)和(4，3)是等边三角形的两个顶点，则求出第三个顶点的坐标，因为原点位于

(i)内部，

(ii)三角形的外部。

解决方案：

Let us considered the third vertex of an equilateral triangle be (x, y).

So, the vertices are A (-4, 3), B (4,3) and C (x, y).

We know that, in equilateral triangle the angle between two

adjacent side is 60 and all three sides are equal.

Therefore, AB = BC = CA

AB² = BC² = CA²                …..(i)

Now, taking first two parts

AB² = BC²

(4 + 4)² + (3 – 3)² = (x – 4)² + (y – 3)²

64 + 0 = x² + 16 – 8x + y² + 9 – 6y

x² + y² – 8x – 6y = 39          …..(ii)

Now, taking first and third parts.

AB² = CA²

(4 + 4)² + (3 – 3)² = (x – 4)² + (y – 3)²

64 + 0 = x² + 16 – 8x + y² + 9 – 6y

x² + y² – 8x – 6y = 39  

On subtracting eq(ii) from (iii), we get 

x = 0

Now, put the value of x in eq(ii), we get

0 + y² – 0 – 6y = 39

y² – 6y – 39 = 0

Therefore, y = $\frac{6±\sqrt{(-6)^2-4(1)(-39)}}{2*1}$

$y=\frac{6±\sqrt{36+156}}{2}\\ y=\frac{6±\sqrt{192}}{2}\\ y=\frac{6±2\sqrt{48}}{2}=3±\sqrt{48}\\ y=3±4\sqrt{3}\\ y=3+4\sqrt{3}or\space 3-4\sqrt{3}$

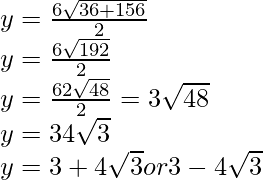
So, the points of third vertex are

(0, 3+√3)or(3 – 4√3)

But it is given that, the origin lies in the interior of the ∆ABC and the x-coordinate of third vertex is zero.

So, y-coordinate of third vertex should be negative.

Hence, the requirement coordinate of third vertex,

C = (0, 3 – 4√3)

问题26.证明点(-3、2)，(-5，-5)，(2，-3)和(4、4)是菱形的顶点。找到这个菱形的区域。

解决方案：

Let us considered the co-ordinates of the vertices A, B, C and D of a rhombus are A (-3, 2), B (-5, -5), C (2, -3) and D (4, 4)

$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ \sqrt{(-5+3)^2+(-5-2)^2}=\sqrt{(-2)^2+(-7)^2}$

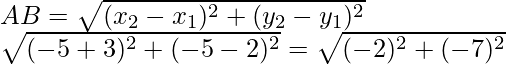
or AB² = (-2)² + (-7)² = 4 + 49 = 53

Similarly, BC² = (2 + 5)² + (-3 + 5)²

= (7)² + (2)² = 49 + 4 = 53

CD² = (4 – 2)² + (4 + 3)²

= (2)² + (7)² = 4 + 48 = 53

 and DA² = (-3 – 4)² + (2 – 4)²

= (-7)² + (-2)² = 49 + 4 = 53

Therefore, we see that AB = BC = CD = DA = √53 

Now diagonals AC = 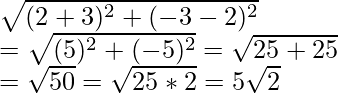$\sqrt{(2+3)^2+(-3-2)^2}\\ =\sqrt{(5)^2+(-5)^2}=\sqrt{25+25}\\ =\sqrt{50}=\sqrt{25*2}=5\sqrt{2}\\$

and diagonal BD = 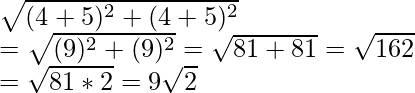$\sqrt{(4+5)^2+(4+5)^2}\\ =\sqrt{(9)^2+(9)^2}=\sqrt{81+81}=\sqrt{162}\\ =\sqrt{81*2}=9\sqrt{2}$

Therefore, sides are equal but diagonal are not equal 

Hence, ABCD is a rhombus 

Now we find the area of rhombus = Product of diagonal/2

= (5√2 × 9√2)/2 

= 9/2 

= 45sq.units

问题27.找到顶点为(3，0)，(-1，-6)和(4，-1)的三角形的外接中心的坐标。另外，找到其圆周。

解决方案：

Let us considered ABC is a triangle whose vertices are A (3, 0), B (-1, -6) and C (4, -1)

So, O be the circumcenter of the triangle ABC and so the co-ordinates be (x, y)

Therefore, OA = OB = OC

OA² = OB² = OC²

Now OA = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\$

OA² = (x₂ – x₁)² + (y₂ – y₁)²

= (x – 3)² + (y – 0)²

= (x – 3)² + y²

OB² = (x + 1)² +(y + 6)²

and OC² = (x – 4)² + (y + 1)²

Therefore, OA² = OB²

(x – 3)² + y² = (x + 1)² + (y + 6)²

x² – 6x + 9 + y² = x² + 2x + 1 + y² + 12y + 36

-6x – 2x – 12y = 1 + 36 – 9

-8x – 12y = 28

2x + 3y = -7 ……..(i)

Therefore, OB² = OC²

(x + 1)² + (y + 6)² = (x – 4)² + (y + 1)²

x² + 2x + 1 + y² + 12y + 36 = x² – 8x + 16 + y² + 2y + 1

2x + 12y + 37 + 8x – 2y = 17

10x + 10y = 17 – 37 = -20

x + y = -2          ……..(ii)

On multiply eq(i) by 1 and (ii) by 2, we get

2x + 3y = -7

2x + 2y = -4

Now, on substituting y = -3, we get

x + y = -2

x – 3 = -2

x = -2 + 3 = 1

Radius = OA = 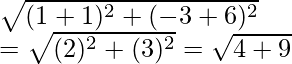$\sqrt{(1+1)^2+(-3+6)^2}\\ =\sqrt{(2)^2+(3)^2}=\sqrt{4+9}$ = √13

问题28.在x轴上找到一个与点(7，6)和(-3，4)等距的点。

解决方案：

The required point is on x-axis

Its ordinate will be O

So, the co-ordinates of the required point P (x, 0)

It is given that the point P is equidistant from the points A (7, 6) and B (-3, 4)

Now AP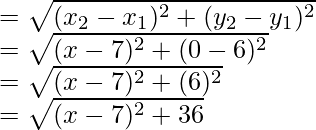$=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(x-7)^2+(0-6)^2}\\ =\sqrt{(x-7)^2+(6)^2}\\ =\sqrt{(x-7)^2+36}$

Therefore, AP² = (x – 7)² + 36

Similarly, BP² = (x + 3)² + (0 – 4)²

= (x + 3)² + 16

Therefore, AP = BP 

AP² = BP²

Therefore, (x – 7)² + 36 = (x + 3)² + 16

x² – 14x + 49 + 36 = x² + 6x + 9 + 16

x² – 14x – x² – 6x = 25 – 85

-20x = -60

x = -60/-20 = 3

Therefore, the required point will be (3, 0)

问题29.(i)证明点A(5，6)，点B(1，5)，点C(2，1)和点D(6，2)是正方形的顶点。

(ii)证明点A(2、3)，B(-2、2)，C(-1，-2)和D(3，-1)是正方形ABCD的顶点。

(iii)命名由点P(√2，√2)，Q(-√2，–√2)和R(-√6，√6)组成的三角形PQR的类型。

解决方案：

(i) Given points are given A (5, 6), B (1, 5), C (2, 1) and D (6, 2) 

Now AB² = (x₂ – x₁)² + (y₂ – y₁)²

= (1 – 5)² + (5 – 6)²

= (-4)² + (-1)² = 16 + 1 = 17

Similarly, BC = (2 – 1)² + (1 – 5)²

= (1)² + (-4)²

= 1 + 16 = 17

CD = (6 – 2)² + (2 – 1)² + (4)² + (1)²

= 16 + 1 = 17

 and DA = (5 – 6)² + (6 – 2)²

= (-1)² + (4)²

= 1 + 16 = 17

Diagonals AC² = (2 – 5)² + (1 – 6)²

= (-3)² + (-5)²

= 9 + 25 

=34

and BD² = (6 – 1)² + (2 – 5)²

= (5)² + (-3)²

= 25 + 9 = 34

 We conclude that

AB = BC = CD = DA and diagonals AC = BD

Hence, ABCD is a square.

(ii) Given points A(2, 3), B(-2, 2), C(-1, -2) and D(3, -1)

$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{()^2+(2-3)^2}\\ =\sqrt{(-4)^2+(-1)^2}\\ =\sqrt{16+1}=\sqrt{17}$

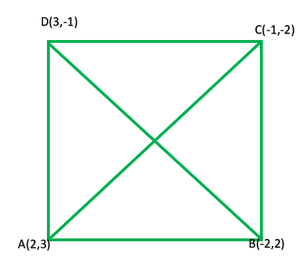
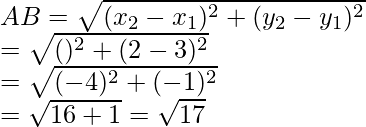
Similarly,

$BC=\sqrt{(-1+2)^2+(-2-2)^2}\\ =\sqrt{(1)^2+(-4)^2}\\ =\sqrt{1+16}=\sqrt{17}\\ CD=\sqrt{(3+1)^2+(-1+2)^2}\\ =\sqrt{(4)^2+(1)^2}\\ =\sqrt{16+1}=\sqrt{17}\\ DA=\sqrt{(2-3)^2+(3+1)^2}\\ =\sqrt{(-1)^2+(4)^2}\\ =\sqrt{1+16}=\sqrt{17}\\ AC=\sqrt{(-1-2)^2+(-2-3)^2}\\ =\sqrt{(-3)^2+(-5)^2}\\ =\sqrt{9+25}=\sqrt{34} \\ BD=\sqrt{(3+2)^2+(-1-2)^2}\\ =\sqrt{(5)^2+(-3)^2}\\ =\sqrt{25+9}=\sqrt{34}$

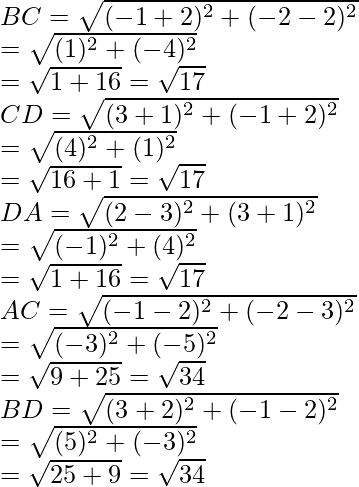
Therefore, AB, BC, CD and DA are equal and diagonals AC and BD are also equal

Hence, ABCD is a square.

(iii) Using distance formula

$PQ=\sqrt{(\sqrt{2}+\sqrt{2})^2+(\sqrt{2}+\sqrt{2})^2}\\ =\sqrt{(2\sqrt{2})^2+(2\sqrt{2})^2}=\sqrt{16}=4\\ PR=\sqrt{(\sqrt{2}+\sqrt{6})^2+(\sqrt{2}-\sqrt{6})^2} \\ =\sqrt{2+6+2\sqrt{12}+2+6-2\sqrt{12}}=\sqrt{16}=4\\ RQ=\sqrt{(-2\sqrt{2}+\sqrt{6})^2+(-2\sqrt{2}-\sqrt{6})^2}\\ =\sqrt{2+6-2\sqrt{12}+2+6+2\sqrt{12}}=\sqrt{16}=4$

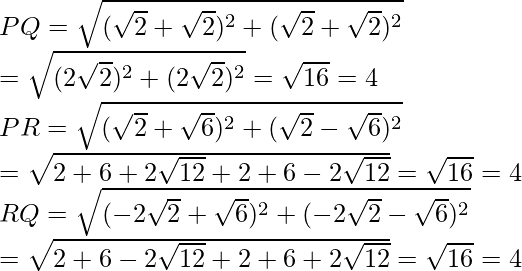
Since, PQ = PR = RQ = 4, so, the point P, Q, R form an equilateral triangle.

问题30.找到x轴上与点(-2，5)和(2，-3)等距的点。

解决方案：

Let us considered point P lies on x-axis

So, the coordinates of point P be (x, 0)

It is given that P is equidistant from A (-2, 5) and B (2, -3)

$AP=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(x+2)^2+(0-5)^2}$

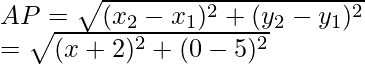
AP² = (x + 2)² + (-5)² 

= (x + 2)² + 25

BP² = (x – 2)² + (0 + 3)² 

= (x – 2)² + 9

AP = BP

So, AP² = BP²

(x + 2)² + 25 = (x – 2)² + 9

x² + 4x + 4 + 25 = x² – 2x + 4 + 9

x² + 4x – x² + 4x = 13 – 29

8x = -16

x = -16/8

x = -2

Hence, the co-ordinates of point P are(-2, 0)

问题31.求x的值，使PQ = QR，其中P，Q和R的坐标分别为(6，-1)，(1、3)和(x，8)。

解决方案：

Given that the co-ordinates of P (6, -1), Q(1, 3), and R(x, 8) 

Also, PQ = QR

By using the distance formula 

D = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

We find the length of PQ and QR

PQ² = (1 – 6)² + (3 + 1)²

= (-5)² + (4)² 

= 25 + 16 = 41

QR² = (x – 1)² + (8 – 3)² 

= (x – 1)² + (5)² = (x – 1)² + 25

It is given that PQ = QR

So PQ² = QR²

41 = (x – 1)² + 25

(x – 1)² = 41 – 25 = 16 = (±4)²

x – 1 = ±4

If x – 1 = 4, then x = 1 + 4 = 5

If x – 1 = -4 then x = -4 + 1 = -3

Hence, the value of x = 5, -3

问题32.证明点(0，0)，(5，5)和(-5，5)是等腰三角形的顶点。

解决方案：

Let us consider ABC is a triangle whose vertices are A(0, 0), B(5, 5), and C(-5, 5)

Now 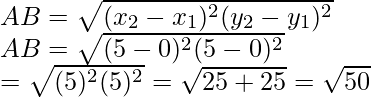$AB=\sqrt{(x_2-x_1)^2(y_2-y_1)^2}\\ AB=\sqrt{(5-0)^2(5-0)^2}\\ =\sqrt{(5)^2(5)^2}=\sqrt{25+25}=\sqrt{50}$

AB² = (√50)² = 50

Similarly, BC² = (-5 – 5)²(5 – 5)²

= (-10)² + (0)² = 100 + 0 = 100

and CA² = (0 + 5)² + (0 – 5)²

= (5)² + (-5)² = 25 + 25 = 50

Here, we conclude that AB = CA

Also, AB² + CA² = 50 + 50 = 100 = BC²

Hence, the triangle ABC is a right triangle.

问题33.如果点P(x，y)与点A(5，1)和点B(1,5)等距，则证明x = y。

解决方案：

Let us consider P(x, y) is equidistant from the points A (5, 1) and B (1,5),

It is given that PA = PB

Also, PA² = PB²

Now, PA=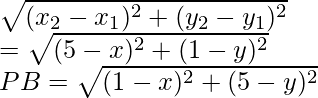$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(5-x)^2+(1-y)^2}\\ PB=\sqrt{(1-x)^2+(5-y)^2}\\$

On squaring both sides, we get

(5 – x)² + (1 – y)² = (1 – x)² + (5 – y)²

25 + x² – 10x + 1 + y² – 2y = 1 + x² – 2x + 25 + y² – 10y

-10x – 2y + 26 = -2x – 10y + 26

-10x – 2y = -2x – 10y

-10x + 2x = -10y + 2y

-8x = -8xy

x = y

问题34.如果Q(0，1)与P(5，-3)和R(x，6)等距，则求出x的值。还要找到距离QR和PR。

解决方案：

Given that Q (0, 1) is equidistant from P (5, -3) and R (x, 6)

So, PQ = RQ

Also, PA² = PB²

Now 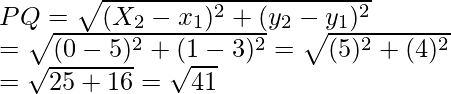$PQ=\sqrt{(X_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(0-5)^2+(1-3)^2}=\sqrt{(5)^2+(4)^2}\\ =\sqrt{25+16}=\sqrt{41}$

PQ² = 41

Similarly, RQ² = (-x)² + (1 – 6)² 

= (-x)² + (-5)² = x² + 25

It is given that PQ = RQ
So, 

x² + 25 = 41 

x² = 41 – 25

x² = (±4)² 

x = ±4

Now, QR = √x² + 25 = √41

So, when x = 4, then 

$PR=\sqrt{(5-4)^2+(-3-6)^2}\\ =\sqrt{(1)^2+(-9)^2}=\sqrt{1+18}=\sqrt{82}$

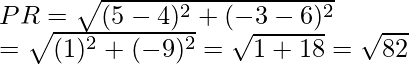
or when x = -4, then

$PR=\sqrt{(5+4)^2+(-3-6)^2}\\ =\sqrt{(9)^2+(-9)^2}=\sqrt{81+81}\\ \sqrt{81*2}=9\sqrt{2}$

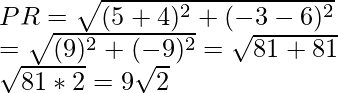
问题35.找到点P(2，-3)与点Q(10，y)之间的距离为10个单位的y值。

解决方案：

Given that the distance between P (2, -3) and Q (10, y) = 10

So, 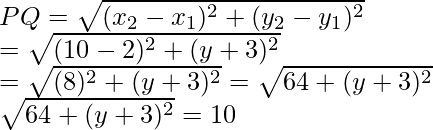$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(10-2)^2+(y+3)^2}\\ =\sqrt{(8)^2+(y+3)^2}=\sqrt{64+(y+3)^2}\\ \sqrt{64+(y+3)^2}=10$

On squaring both side we get

64 + (y + 3)² = 100

(y + 3)² = 100 – 64

(y + 3)² = 36

y + 3  = (±6)² 

So, when y + 3 = 6, then y = 6 – 3 = 3

Or when y + 3 = -6, then y = -6 – 3 = -9

Hence, y = 3, -9

问题36.如果点P(k – 1，2)与点A(3，k)和点B(k，5)等距，则求出k的值。

解决方案：

Given that the point P (k – 1, 2) is equidistant from A (3, k) and B (k, 5)

So, PA = PB

Also, PA² = PB²

(k – 1 – 3)² + (2 – k)² = (k – 1 – k)² + (2 – 5)²

(k – 4)² + (2 – k)² = (-1)² + (-3)²

k² – 8k + 16 + 4 – 4k + k² = 1 + 9

2k² – 12k + 20 – 10 = 0

2k² – 12k + 10 = 0

k² – k – 5k + 5 = 0

k(k – 1) – 5(k – 5) = 0

(k – 1)(k – 5) = 0

Either k – 1 = 0, then k = 1

or k – 5 = 0, then k = 5

Hence, k = 1, 5

问题37.如果点A(0，2)与点B(3，p)和点C(p，5)等距，则找到p。另外，找到AB的长度。

解决方案：

Given that point A (0, 2) is equidistant from B (3, p) and C (p, 5)

So, AB = AC

Also, AB² = AC²

(0 – 3)² + (2 – p)² = (0 – p)² + (2 – 5)²

9 + (2 – p)² = p² + 9

9 + 4 + p² – 4p = p² + 9

p² – 4p + 13 – p² – 9 = 0

-4p – 4 = 0

-4p = -4

p = -4/-4 = 1

p = 1

and AB = 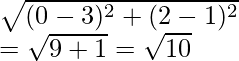$\sqrt{(0-3)^2+(2-1)^2}\\ =\sqrt{9+1}=\sqrt{10}$

问题38.通过以下几点来命名形成的四边形(如果有的话)，并给出回答的理由：

(i)A(-1，-2)，B(1，0)，C(-1，2)，D(-3，0)

(ii)A(-3、5)，B(3、1)，C(0、3)，D(-1，-4)

(iii)A(4、5)，B(7、6)，C(4、3)，D(1、2)

解决方案：

(i) Given points are A (-1, -2), B (1, 0), C (-1, 2), D (-3, 0)

Now $AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

AB² = (x₂ – x₁)²  + (y₂ – y₁)² 

= (1 + 1)² + (0 + 2)² 

= (2)² + (2)² 

= 4 + 4 = 8

Similarly, BC² = (-1 – 1)² + (2 – 0)² 

= (-2)² + (2)² 

= 4 + 4 = 8

CD² = (-3 + 1)² + (0 – 2)² 

= (-2)² + (-2)²

= 4 + 4 = 8

DA² = (-1 + 3)² + (-2 + 0)² 

= (2)² + (-2)² 

= 4 + 4 = 8

Diagonal AC² = (-1 + 1)² + (2 + 2)²

= (0)² + (4)² = 0 + 16 = 16

and BD² = (-3 – 1)² + (0 – 0)² = (-4)² + (0) = 16

Therefore, the sides are equal and diagonals are also equal

Hence, the quadrilateral ABCD is a square.

(ii) Given points are A (-3, 5), B (3, 1), C (0, 3), D (-1, -4)

Now AB$=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

AB² = (x₂ – x₁)²  + (y₂ – y₁)² 

= (3 + 3)² + (1 – 5)² 

= (6)² + (-4)² 

= 36 + 16 = 52

Similarly, BC² = (0 – 3)² + (3 – 1)² 

= (-3)² + (2)²

= 9 + 4 = 13

CD² = (-1 – 0)² + (-4 – 3)² 

= (-1)² + (-7)²

= 1 + 49 = 50

DA² = (-3 + 1)² + (5 + 4)² 

= (-2)² + (9)² 

= 4 + 81 = 85

Diagonal AC² = (0 + 3)² + (3 – 5)² = (3)² + (-2)² = 9 + 4 = 13

In triangle ABC

The length of AB = √52, AC = √13, BC = √13 

AC + BC = √13 + √13 = 2√13 

= √4 * 13 = √52 

AC + BC = AB    

Triangle ABC is not possible 

Hence, ABCD is not a quadrilateral

(iii) Points A (4, 5), B (7, 6), C (4, 3), D (1, 2)

Now AB$=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

AB² = (x₂ – x₁)²  + (y₂ – y₁)² 

= (7 – 4)² + (6 – 5)² 

= (3)² + (1)²

= 9 + 1 = 10

Similarly, BC² = (4 – 7)² + (3 – 6)²

= (3)² + (-3)² = 9 + 9 = 18

CD² = (1 – 4)² + (2 – 3)² 

= (-3)² + (-1)² 

= 9 + 1 = 10

DA² = (4 – 1)² + (5 – 2)² = (3)² + (3)² = 9 + 9 = 18

Here AB = CD and BC = DA

Diagonal AC² = (4 – 4)² + (3 – 5)²

= (0)² + (-2)²

= 0 + 4 = 4

and BD² = (1 – 7)² + (2 – 6)² = (-6)² + (-4)²

= 36 + 16 = 52

Hence the opposite sides are equal and diagonals are not equal.

So, ABCD is a parallelogram.

问题39.找到连接点(7，1)和(3，5)的线段的垂直平分线方程。

解决方案：

Let the given points are A (7, 1) and B (3, 5) and mid point be M

Coordinates of mid-point AB = ((7 + 3)/2, (1 + 5)/2) = (5, 3)

Now slope of AB(m₁)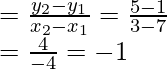$=\frac{y_2-y_1}{x_2-x_1}=\frac{5-1}{3-7}\\ =\frac{4}{-4}=-1$

Slope of perpendicular to AB(m₂) = -1/m₁ = -(-1) = -1 

So, the equation of the perpendicular line passing through multiple y – y₁ = m(x – x₁)

y – 3 = 1(x – 5)

y – 3 = x – 5

x – y = -3 + 5

x – y = 2