第 10 类 RD Sharma 解决方案 – 第 2 章多项式 – 练习 2.3

问题 1. 应用除法算法求下列各式中 f(x) 除以 g(x) 的商 q(x) 和余数 r(x)：

(i) f(x) = x ³ – 6x ² + 11x – 6, g(x) = x ² + x + 1

(ii) f(x) = 10x ⁴ + 17x ³ – 62x ² + 30x – 105, g(x) = 2x ² + 7x + 1

(iii) f(x) = 4x ³ + 8x ² + 8x + 7, g(x) = 2x ² – x + 1

(iv) f(x) = 15x ³ – 20x ² + 13x – 12, g(x) = x ² – 2x + 2

解决方案：

(i) Here we have to divide f(x) = x³ – 6x² + 11x – 6 by g(x) = x² + x + 1 

So, to get quotient q(x) and remainder r(x), we use division algorithm

Therefore,

Remainder r(x) = 17x – 1

Quotient q(x) = x – 7

(ii) Here we have to divide f(x) = 10x⁴ + 17x³ – 62x² + 30x – 105 by g(x) = 2x² + 7x + 1

So, to get quotient q(x) and remainder r(x), we use division algorithm

Therefore,

Remainder r(x) = 53x – 1

Quotient q(x) = 5x² – 9x – 2

(iii) Here we have to divide f(x) = 4x³ + 8x² + 8x + 7 by g(x) =2x² – x + 1

So, to get quotient q(x) and remainder r(x), we use division algorithm

Therefore,

Remainder r(x) = 11x + 2

Quotient q(x) = 2x – 5

(iv) f(x) = 15x³ – 20x² + 13x – 12, g(x) = x² – 2x + 2

Here we have to divide f(x) =  15x³ – 20x² + 13x – 12 by g(x) = x² – 2x + 2

So, to get quotient q(x) and remainder r(x), we use division algorithm

Therefore,

Remainder r(x) = 3x + 32

Quotient q(x) = 15x + 10

问题 2. 通过应用除法算法检查第一个多项式是否是第二个多项式的因子：

(i) g(t) = t ² – 3； f(t) = 2t ⁴ + 3t ³ – 2t ² – 9t – 12

(ii) g(x) = x ² – 3x + 1； f(x) = x ⁵ – 4x ³ + x ² + 3x + 1

(iii) g(x) = 2x ² – x + 3； f(x) = 6x ⁵ - x ⁴ + 4x ³ - 5x ² - x - 15

解决方案：

(i) Here, we have to check whether g(t) = t² – 3 is a factor of f(t) = 2t⁴ + 3t³ – 2t² – 9t – 12

So, by using division algorithm, we get

As the remainder left is 0.

Therefore,

g(t) = t² – 3 is a factor of f(t) = 2t⁴ + 3t³ – 2t² – 9t – 12

(ii) Here, we have to check whether g(x) = x² – 3x + 1 is a factor off(x) = x⁵ – 4x³ + x² + 3x + 1

So, by using division algorithm, we get

As the remainder left is 2.

Therefore,

g(x) = x² – 3x + 1 is not a factor of  f(x) = x⁵ – 4x³ + x² + 3x + 1

(iii) Here, we have to check whether g(x) = 2x² – x + 3 is a factor of f(x) = 6x⁵ − x⁴ + 4x³ – 5x² – x – 15

So, by using division algorithm, we get

As the remainder left is 0.

Therefore,

g(x) = 2x² – x + 3 is a factor of f(x) = 6x⁵ − x⁴ + 4x³ – 5x² – x – 15

问题 3. 获得多项式 f(x) = f(x) = 2x ⁴ + x ³ – 14x ² – 19x – 6 的所有零点，如果它的两个零点是 -2 和 -1。

解决方案：

Given: f(x) = 2x⁴ + x³ – 14x² – 19x – 6

Here we have given the two zeroes of the polynomial that are -2 and -1, 

Hence, its factors will be  (x + 2) and (x + 1)

Further,

(x + 2)(x + 1) = x² + x + 2x + 2 = x² + 3x + 2

So, by using division algorithm, we get

f(x) = 2x⁴ + x³ – 14x² – 19x – 6 = (2x² – 5x – 3)(x² + 3x + 2)

= (2x + 1)(x – 3)(x + 2)(x + 1)

Hence, the factors of f(x) = 2x⁴ + x³ – 14x² – 19x – 6 are (2x + 1), (x – 3), (x + 2), (x + 1)

Therefore, the zeroes of the polynomial are -1/2, 3, -2, -1

问题 4. 获得 f(x) = x ³ + 13x ² + 32x + 20 的所有零，如果其中一个零是 -2。

解决方案：

We have been given the zero of the polynomial f(x) = x³ + 13x² + 32x + 20 is -2. 

Hence, its factor is (x + 2).

So, by using division algorithm, we get

Thus, 

f(x) = x³ + 13x² + 32x + 20 

= (x² + 11x + 10)(x + 2)

= (x² + 10x + x + 10)(x + 2)

= (x + 10)(x + 1)(x + 2)

Hence, the factors of f(x) = x³ + 13x² + 32x + 20 are (x + 10), (x + 1), (x + 2)

Thus, the zeroes of the polynomial are -1, -10, -2.

问题 5. 获得多项式 f(x) = x ⁴ – 3x ³ – x ² + 9x – 6 的所有零点，如果它的两个零点是 -√3 和 √3。

解决方案：

Here, we are given two zeros of the polynomial f(x) = x⁴ – 3x³ – x² + 9x – 6 that are -√3 and √3.

Thus, the factors are (x + √3​)(x − √3​) ⇒ x² – 3.

So, by using division algorithm, we get

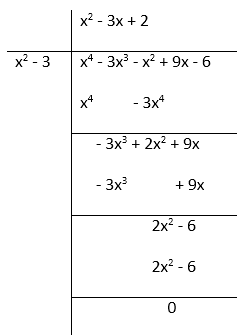
Hence, 

f(x) = x⁴ – 3x² – x² + 9x – 6 = (x² – 3)(x² – 3x + 2)

(x + √3)(x – √3)(x² – 2x – 2 + 2)

= (x + √3)(x – √3)(x – 1)(x – 2)

Thus, the factors of f(x) = x⁴ – 3x³ – x² + 9x – 6 are (x + √3)(x – √3)(x – 1)(x – 2).

Therefore, the zeroes of the polynomial are -√3, √3, 1, 2.

问题 6. 获得多项式 f(x) = 2x ⁴ – 2x ³ – 7x ² + x – 1 的所有零点，如果它的两个零点是 -√3/2 和 √3/2。

解决方案：

Here, we are given two zeros of the polynomial f(x) = 2x⁴ – 2x³ – 7x² + x – 1 that are -√3/2 and √3/2.

Thus, the factors are $\left(x-\sqrt\frac{3}{2}\right) \left(x+\sqrt\frac{3}{2}\right)$ ⇒ x² – 3/2.

So, by using division algorithm, we get

Hence, 

$f(x) = 2x^4- 2x^3-7x^2+ x - 1=\left(x-\sqrt\frac{3}{2}\right) \left(x+\sqrt\frac{3}{2}\right)(2x^2-2x-4)\\ \left(x-\sqrt\frac{3}{2}\right)\left(x+\sqrt\frac{3}{2}\right)(2x^2-4x+2x-4)\\ \left(x-\sqrt\frac{3}{2}\right)\left(x+\sqrt\frac{3}{2}\right)(x+2)(x-2)$

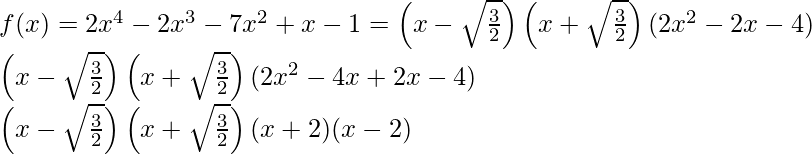
Factors of f(x) = 2x⁴ – 2x³ – 7x² + x – 1 are $\left(x-\sqrt\frac{3}{2}\right),\ \left(x+\sqrt\frac{3}{2}\right),\ (x+2),\ (x-2)$.

Thus, the zeroes of the polynomial are -1, 2, -√3/2 and √3/2.

问题 7. 找到多项式 x ⁴ + x ³ – 34x ² – 4x + 120 的所有零点，如果它的两个零点是 2 和 – 2。

解决方案：

Here, we are given two zeros of the polynomial x⁴ + x³ – 34x² – 4x + 120 that are 2 and -2.

Thus, the factors are (x + 2)(x – 2)⇒ x² – 4.

So, by using division algorithm, we get

Hence,

x⁴ + x³ – 34x² – 4x + 120 = (x² – 4)(x² + x – 30)

= (x – 2)(x + 2)(x² + 6x – 5x – 30)

=  (x – 2)(x + 2)(x + 6)(x – 5)

So, the factors of x⁴ + x³ – 34x² – 4x + 120 are (x – 2), (x + 2), (x + 6), (x – 5)

Thus, the zeroes of the polynomial = x = 2, – 2, – 6, 5

问题 8. 找到多项式 2x ⁴ + 7x ³ – 19x ² – 14x + 30 的所有零点，如果它的两个零点是 √2 和 -√2。

解决方案：

Here, we are given two zeros of the polynomial 2x⁴ + 7x³ – 19x² – 14x + 30² that are √2 and -√2.

Thus, the factors are (x + √2)(x – √2) ⇒ x² – 2.

So, by using division algorithm, we get

Hence, 

2x⁴ + 7x³ – 19x² – 14x + 30 = (x² – 2)(2x² + 7x – 15)

= (2x² + 10x – 3x – 15)(x + √2)(x – √2)

= (2x – 3)(x + 5)(x + √2)(x – √2)

So, the factors of 2x⁴ + 7x³ – 19x² – 14x + 30 are (2x – 3), (x + 5), (x + √2), (x – √2) 

Thus, the zeroes of the polynomial is √2, -√2, -5, 3/2.

问题 9. 找到多项式 f(x) = 2x ³ + x ² – 6x – 3 的所有零点，如果其中两个零点是 -√3 和 √3。

解决方案：

Here, we are given two zeros of the polynomial f(x) = 2x³ + x² – 6x – 3 that are -√3 and √3.

Thus, the factors are (x + √3)(x – √3) ⇒ x² – 3.

So, by using division algorithm, we get

Hence, 

f(x) = 2x³ + x² – 6x – 3 

= (x² – 3)(2x + 1)

= (x + √3)(x – √3)(2x + 1)

Factors of f(x) = 2x³ + x² – 6x – 3 are (x + √3), (x – √3), 2x + 1

Thus, the zeroes for the given polynomial are √3, -√3, -1/2

问题 10. 找到多项式 f(x) = x ³ + 3x ² – 2x – 6 的所有零点，如果它的两个零点是 √2 和 -√2。

解决方案：

Here, we are given two zeros of the polynomial f(x) = x³ + 3x² – 2x – 6 that are √2 and -√2.

Thus, the factors are (x + √2)(x – √2)⇒ x² – 2.

So, by using division algorithm, we get

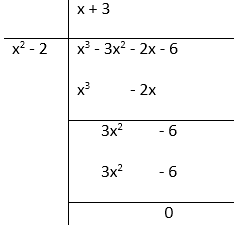
Hence,

f(x) = x³ + 3x² – 2x – 6 

= (x² – 2)(x + 3)

= (x + √2)(x – √2)(x + 3)

Factors of f(x) = x³ + 3x² – 2x – 6 are (x + √2), (x – √2), (x + 3)

Thus, the zeroes of the given polynomial is -√2, √2, and – 3.

问题 11. 多项式 f(x) = x ⁴ + 2x ³ – 2x ² + x - 1 必须添加什么，以使生成的多项式可以被 g(x) = x ² + 2x - 3 整除。

解决方案：

Here we have to add to the polynomial f(x) = x⁴ + 2x³ – 2x² + x − 1 so that the 

resulting polynomial is exactly divisible by g(x) = x² + 2x − 3.

So, divide f(x) = x⁴ + 2x³ – 2x² + x − 1 by g(x) = x² + 2x − 3 to get the answer.

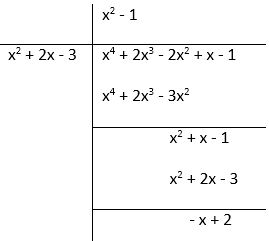
As the remainder left is (x – 2) to get the resulting polynomial exactly divisible by 

g(x) = x² + 2x − 3 we must add (x – 2) to f(x) = x⁴ + 2x³ – 2x² + x − 1.

问题 12. 必须从多项式 f(x) = x ⁴ + 2x ³ – 13x ² –12x + 21 中减去什么，以便得到的多项式可以被 g(x) = x ² – 4x + 3 整除。

解决方案：

Here we have to subtract to the polynomial f(x) = x⁴ + 2x³ – 13x² – 12x + 21 

so that the resulting polynomial is exactly divisible by g(x) = x² – 4x + 3.

So, divide f(x) = x⁴ + 2x³ – 13x² – 12x + 21 by  g(x) = x² – 4x + 3 to get the answer.

As the remainder left is (2x – 3) to get the resulting polynomial exactly divisible by 

g(x) = x² – 4x + 3 we must add (2x – 3) to f(x) = x⁴ + 2x³ – 13x² – 12x + 21.

问题 13. 假设 √2 是三次多项式 f(x) = 6x ³ + √2x ² – 10x – 4√2 的零，求它的另外两个零。

解决方案：

Here, we are given that √2 is the zero of the cubic polynomial

f(x) = 6x³ + √2x²– 10x – 4√2, thus, factor of the polynomial is (x – √2) 

So, by using division algorithm, we get

Hence,

f(x) = 6x³ + √2x² – 10x – 4√2

= (x – √2)(6x² + 7√2x + 4)

= (x – √2)(6x² + 4√2x + 3√2x + 4)

= (x – √2)(3x + 2√2)(2x + √2)

The factors of f(x) = 6x³ + √2x²– 10x – 4√2 are (x – √2), (3x + 2√2), (2x + √2)

Therefore, the zeros of the polynomial are -2√2/3, -√2/2, √2 

问题 14. 假设 x – √5 是三次多项式 x ³ – 3√5x ² + 13x – 3√5 的因数，找出多项式的所有零点。

解决方案：

Here, we have x – √5 as factor of the cubic polynomial x³ – 3√5x² + 13x – 3√5

To find all the zeros of the polynomial, we have to divide the polynomial x³ – 3√5x² + 13x – 3√5 by the factor x – √5 

Hence,

x³ – 3√5x² + 13x – 3√5

= (x – √5)(x² – 2√5 + 3)

= (x – √5)(x – (√5 + √2))(x – (√5 – √2))

So, the factors of the cubic polynomial x³ – 3√5x² + 13x – 3√5 are (x – √5), (x – (√5 + √2)), (x – (√5 – √2))

Therefore, the zero of the polynomial are √5, (√5 – √2), (√5 + √2)