第 10 类 RD Sharma 解决方案 – 第 12 章三角函数的一些应用 – 练习 12.1 |设置 2

问题27，一座电视塔垂直矗立在一条河流的河岸上。从塔对面的对岸一点，塔顶的仰角为60°。从同一堤岸上距该点20m处，塔顶仰角为30°。求塔的高度和河流的宽度。

解决方案：

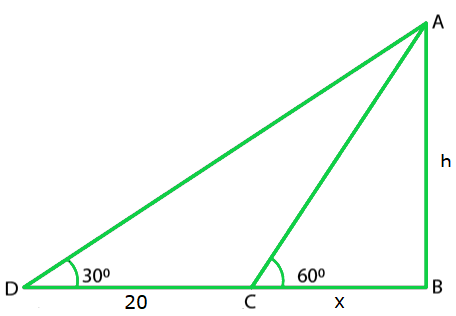
Let us considered AB be the T.V tower of height ‘h’ m on the bank of river and 

D be the point on the opposite side of the river. 

So, the angle of elevation at the top of the tower is 30°

So, AB = h and BC = x

And, it is given that CD = 20 m

So, 

In ΔACB

tan 60^o = AB/BC

√3x = h

x = h/√3

Now, in ΔDBA,

tan 30^o = AB/BD 

1/√3 = h / (20 + x)

√3h = 20 + x

√3h – h/√3 = 20

2h/√3 = 20

h = 10√3 m

And,

x = h/√3

x = 10√3/ √3

x = 10

Hence, the height of the tower is 10√3 m and width of the river is 10 m.

问题 28. 从 7 m 高的建筑物顶部，电缆顶部的仰角为 60°，其脚的下倾角为 45°。确定塔的高度。

解决方案：

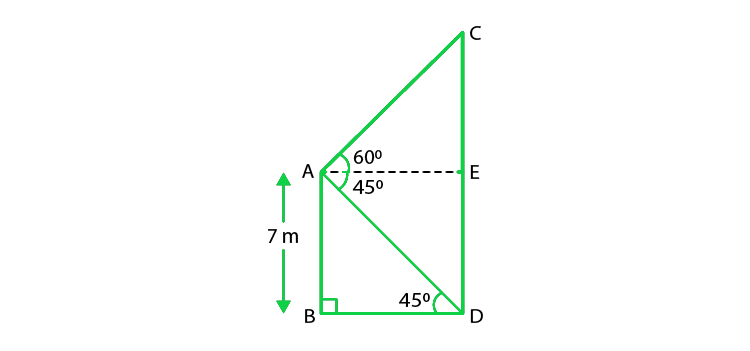
Given that, the height of the building(AB) = 7 m 

Let us considered the height of the cable tower is CD,

So, the angle of elevation of the top of the cable tower from the top of the building = 60°,

Angle of depression of the bottom of the building from the top of the building= 45°,

From the figure we conclude that,

ED = AB = 7 m

And,

CD = CE + ED

So, In ΔABD, 

AB/ BD = tan 45°

AB = BD = 7

BD = 7

Now, in ΔACE,

AE = BD = 7

And, tan 60° = CE/AE

√3 = CE/ 7

CE = 7√3 m

So, CD = CE + ED = (7√3 + 7)= 7(√3 + 1) m

Hence, the height of the cable tower is 7(√3 + 1)m

问题 29. 从 75 m 高的灯塔顶部观察，两艘船的俯角分别为 30°和 45°。如果在灯塔的同一侧，一艘船正好在另一艘船的后面，求两艘船之间的距离。

解决方案：

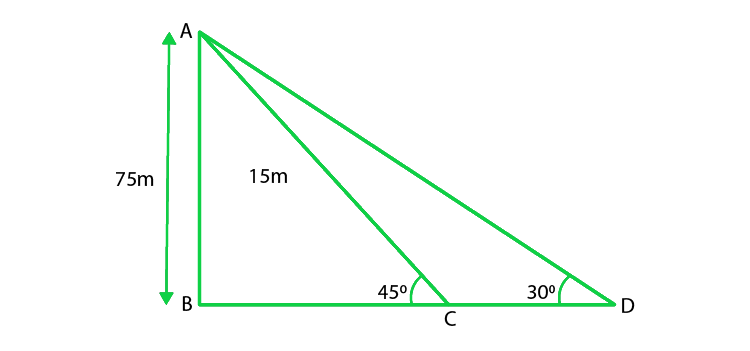
Given that, the height of the lighthouse(AB) = 75m,

The angle of depression of ship 1, α = 30°,

The angle of depression of bottom of the tall building, β = 45°,

From the figure,

Let us considered distance between ships(CD) = x m,

So, In ΔABD, 

tanα = AB/BD

tan 30^o = 75/(x + BC)

x + BC = 75√3             ……(i)

So, In ΔABC, 

tanβ = AB/BC

tan45^o = 75/BC 

BC = 75         ……(ii)

Now on substituting eq(ii) in eq(i), we get

x + 75 = 75√3

x = 75(√3 – 1)

Hence, the distance between the two ships is 75(√3 – 1) m

问题 30. 楼顶与塔脚的仰角为 30°，塔顶与楼脚的仰角为 60°。如果塔高 50 m，求建筑物的高度。

解决方案：

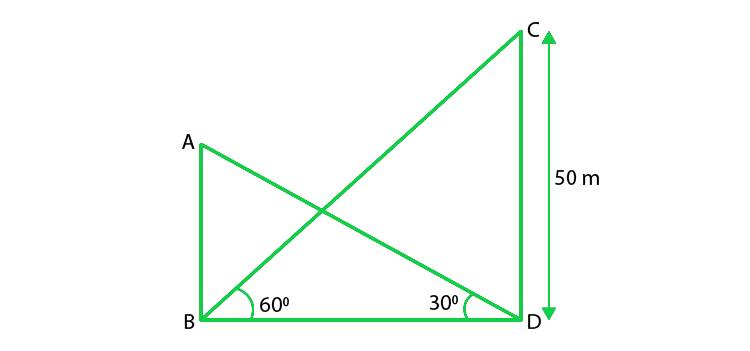
Let’ us considered AB be the building and CD be the tower.

So, according to the question, given that

The angle of elevation of the top of the building from the foot of the tower = 30°,

And, the angle of elevation of the top of the tower from the foot of the building = 60°,

Height of the tower = CD = 50 m,

So, In ΔCDB,

CD/ BD = tan 60°

50/ BD = √3

BD = 50/√3 …. (i)

Next in ΔABD,

AB/ BD = tan 30°

AB/ BD = 1/√3

AB = BD/ √3

AB = 50/√3/ (√3)              (From eq(i))

AB = 50/3

Hence, the height of the building is 50/3 m.

问题 31. 从跨河桥上的一点看，河对岸两岸的倾角分别为 30°和 45°。如果桥距河岸 30 m 高，求河流的宽度。

解决方案：

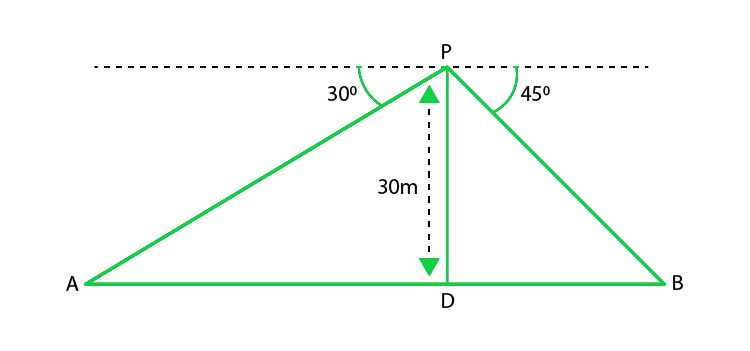
According to the question, given that

The height of the bridge from the bank = 30 m 

Let us considered A and B represent the points on the bank on opposite sides of the river. 

So, AB is the width of the river.

Now, P is a point on the bridge which is 30 m high from the banks.

From the figure,

AB = AD + DB

In ΔAPD,

Given that, ∠A = 30^o

So, tan 30^o = PD/ AD

1/√3 = PD/ AD

AD = √3(30)

AD = 30√3 m

Now, in ΔPBD,

∠B = 45^o

So, tan 45^o = PD/ BD

1 = PD/ BD

BD = PD

BD = 30 m

As we know that, AB = AD + DB = 30√3 + 30 = 30(√3 + 1)

Hence, the width of the river is 30(1 + √3) m

问题 32. 在 80 m 宽的道路两侧，两根等高的杆相对立。从道路上它们之间的一点看，杆顶的仰角分别为60°和30°。求两极的高度和点到两极的距离。

解决方案：

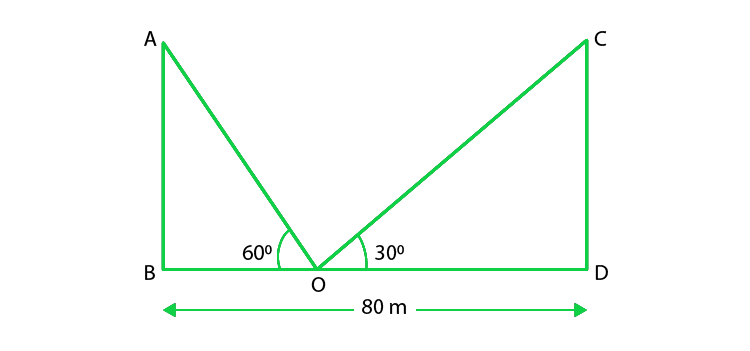
According to the question, given that

The distance between the poles(BD) = 80 m 

The angles of elevation to the top of the points is 60^o and 30^o

Let us considered AB and CD be the poles and O is the point on the road.

From the figure,

In ΔABO,

AB/ BO = tan 60°

AB/ BO = √3

BO = AB/ √3         …….(i)

So, in ΔCDO,

CD/ DO = tan 30^o

CD/ (80 – BO) = 1/ √3

√3CD = 80 – BO

√3AB = 80 – (AB/√3)              (Since AB = CD and using eq(i))

3AB = 80√3 – AB

4AB = 80√3

AB = 20√3

So, BO = 20√3/(√3) = 20 m

And, DO = BD – BO = 80 – 20 = 60

Hence, the height of the poles is 20√3 m and 

the distances of the points from the poles are 20m and 60 m.

问题 33. 一名男子坐在河中小岛上一棵高大的树上，高 20 m，观察河两岸的两根柱子正对，与树脚成一直线。如果从人坐在河两岸的树上的点开始，杆子的脚下角分别为60°和30°。求河流的宽度。

解决方案：

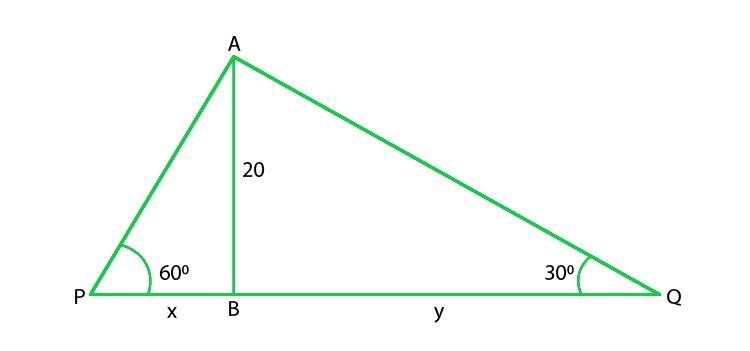
From the given figure,

Let’s width of river = PQ = (x + y) m

Height of tree (AB) = 20 m

So, in ΔABP,

tan 60^o = AB/ BP

√3 = 20/ x

x = 20/ √3 m

In ΔABQ,

tan 30^o = AB/ BQ

1/ √3 = 20/ y

y = 20√3

So, (x + y) = 20/ √3 + 20√3

[20 + 20(3)]/ √3 = 80/√3

Hence, the width of the river is 80/√3 m.

问题 34. 一个垂直的塔架在一个水平面上，上面有一个高度为 7m 的旗杆。从平面上的一点看，旗杆底部的仰角为30°，旗杆顶部的仰角为45°。求塔的高度。

解决方案：

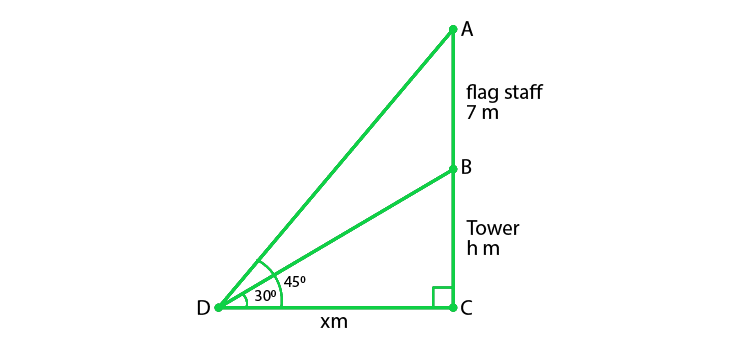
According to the question,

The length of the flagstaff = 7 m

And the angles of elevation of the top and bottom of the flagstaff from point D are 45° and 30° respectively.

Let us considered the height of the tower (BC) = h m

And, DC = x m

So, in ΔBCD

tan 30° = BC/DC

1/ √3 = h/ x

x = h√3    ………(i)

And, in ΔACD

tan 45°  = AC/ DC

1 = (7 + h)/ x

x = 7 + h

h√3 = 7 + h                       (from eq(i))

h(√3 – 1) = 7

h = 7/(√3 – 1)

Now, on rationalizing the denominator we get

h = 7(√3 + 1)/ 2 = 7(1.732 + 1)/2 = 9.562

Hence, the height of the tower is 9.56 m

问题 35. 当太阳高度为 30° 时，发现在水平面上的塔的阴影长度比 30° 时长 2 倍米。证明塔的高度是 x(√3 + 1) 米。

解决方案：

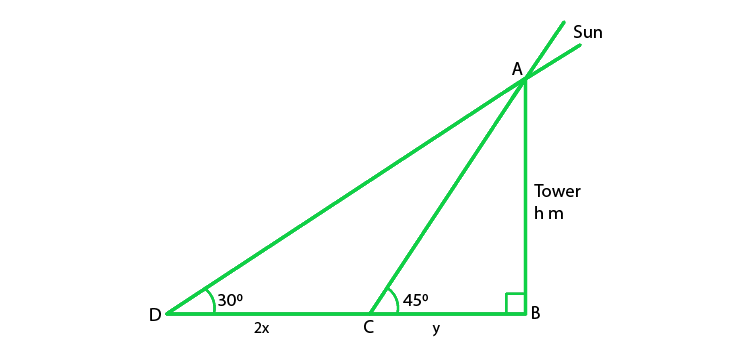
According to the question,

CD = 2x, ∠D = 30°, and ∠C = 45°

Let us considered the height of the tower (AB) = h m,

And the distance BC = y m,

So, in ΔABC

tan 45° = AB/BC

1 = h/y

y = h

So, in ΔABD

tan 30° = AB/BD

1/√3 = h/ (2x + y)

2x + y = √3h

2x + h = √3h

2x = (√3 – 1)h

h = 2x/ (√3 – 1) x (√3 + 1)/ (√3 + 1)

h = 2x (√3 + 1)/(3-1) = 2x (√3 + 1)/2 = x (√3 + 1)

Hence, the height of the tower is x (√3 + 1) m

Hence Proved

问题 36. 一棵树因暴风雨而折断，折断的部分弯曲，使树顶接触地面，与地面成 30° 角。从树脚到顶部接触地面的距离为10米。求树的高度。

解决方案：

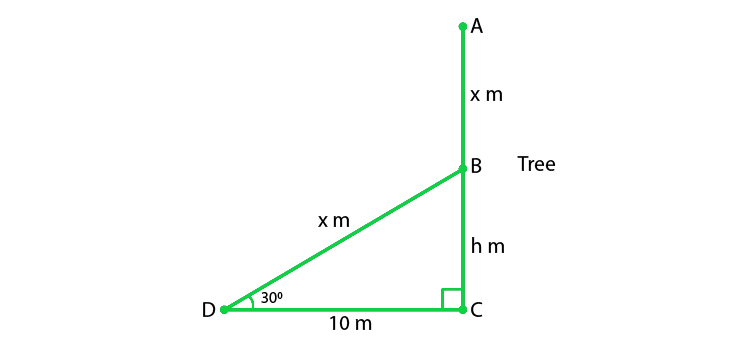
Let us considered AC be the height of the tree which is (x + h) m

Given that, the broken portion of the tree is making an angle of 30° with the ground.

From the given figure,

In ΔBCD, 

tan 30^o = BC/ DC

1/√3 = h/ 10

h = 10/ √3

Now, in ΔBCD

cos 30^o = DC/BD

√3/2 = 10/x

x = 20/√3 m

So,

x + h = 20/√3 + 10/√3 = 30/√3

10√3 = 10(1.732) = 17.32

Hence, the height of the tree is 17.32 m

问题 37. 气球通过与水平面成 60° 角的长度为 215 m 的电缆连接到气象地面站。确定气球离地面的高度。假设电缆没有松弛。

解决方案：

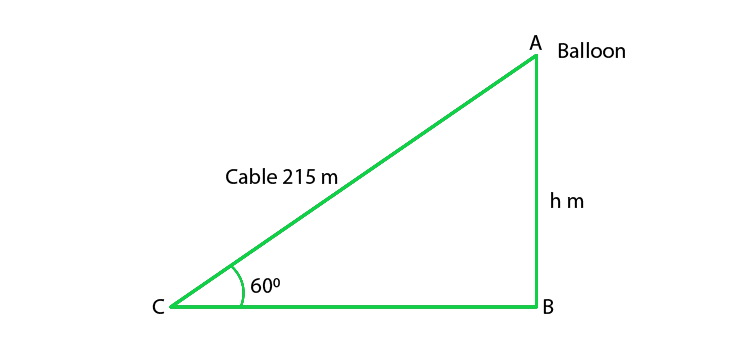
Let us considered the height of the balloon from the ground = h m

Given that, the length of the cable = 215 m, 

and the inclination of the cable is 60^o.

So, 

In ΔABC

sin 60^o = AB/ AC

√3/2 = h/215

h = 215√3/2 = 185.9m

Hence, the height of the balloon from the ground is 186m (approx).

问题 38. 悬崖两侧 80 m 高的两个人观察到悬崖顶部的仰角分别为 30°和 60°。找出两人之间的距离。

解决方案：

Let us considered CL be the cliff and A and B are two men on either side of the cliff 

And they are making angles of elevation with C as 30° and 60° 

It is given that, the height of cliff CL = 80 m

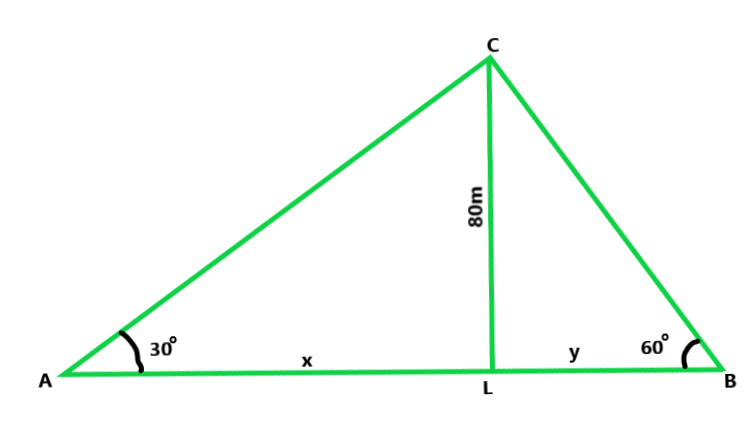
Let us assume AL = x and BL = y

Now in ΔACL,

tan 30^o = 80/x 

x = 80√3

Similarly, in ΔBCL

tan 60^o = CL/BL = √3 = 80/y

y = 80/√3

Hence, the distance between two men,

x + y = 80√3 + 80/√3 

240+80 / √3 = 320/√3

On rationalize the value, we get,

320√3 / 3 = 184.746m

问题 39. 当垂直杆的阴影长度等于其高度时，求太阳的仰角（太阳的高度）。

解决方案：

Let us considered the height of pole AB = h m,

Then the height of shadow = h m

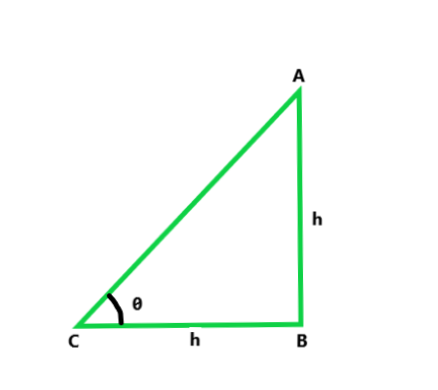
Lets us considered the angle of elevation be θ,

So, In ΔABC,

tan θ = AB/BC = h/h = 1

tan θ = 1 = tan 45^o

Hence, θ = 45^o

问题 40. 一架飞机在 210 m 的高度飞行。在这个高度上飞行的某个瞬间，河两岸相反方向的直线上的两点的俯角分别为 45° 和 60°。求河流的宽度。 （使用√3 = 1.73）

解决方案：

According to the question,

The height of the airplane = 210 m

Let us considered that, AB is the height of the airplane and 

C and D are the points on the opposite banks of a river.

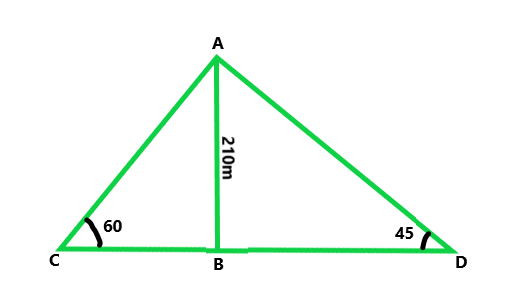
So, the angle of elevation of A are 45° and 60°

Let us considered CB = x and BD = y

In ΔABD,

tan θ = P/B

tan 45^o = AB/BD = 1 = AB/BD

210/BD = 1

BD = 210 m 

Similarly, In ΔABC,

tan 60^o = AB/CB = √3 = 210/CB

CB = 210/√3

On rationalize the value we get,

CB = 70√3 m = 121.10m

So, the width of river = CB + BD

= 121.10 + 210 

= 331.10m

问题41、烟囱顶距塔顶的仰角为60°，烟囱脚距塔顶的俯仰角为30°。如果塔的高度是 40 m，求烟囱的高度。根据污染控制规范，排烟烟囱的最低高度应为100 m。说明上述烟囱的高度是否符合污染标准。这个问题讨论了什么价值？

解决方案：

 Let us considered, CD be the tower and AB be the chimney 

So, the angle of elevation of the top of the tower with the top of the chimney is 60° and 

the foot of chimney with the top of the tower is 30°

So, it is given that CD = 40 m

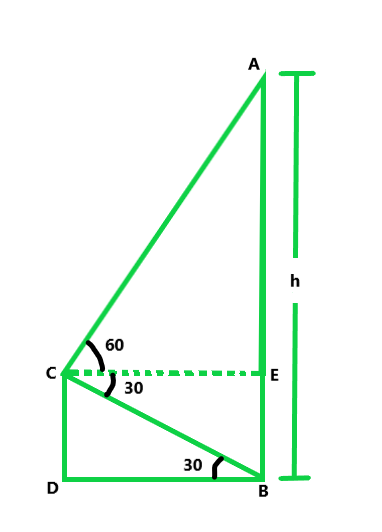
From the given figure,

CE|| DB

So, CE = DB and EB = CD = 40

Now in △BCD

tan 30° = 40/DB = 1/√3

DB = 40√3             …….(i)

Now, in △ACE

tan 60° = AE/CE = √3 = (h – 40)/DB

DB = (h-40)/√3           …….(ii)

From eq(i) and (ii), we get

40√3 = (h – 40)/√3 = 120 + 40 = 160m

Hence, the height of the chimney is 160m.

问题 42. 两艘船在海中，在灯塔的两侧，船和灯塔在同一条直线上。从灯塔顶部观察两艘船的俯角分别为60°和45°。如果灯塔的高度是 200 m，求两船之间的距离。 （使用√3 = 1.73）

解决方案：

Let us considered that, AB be the lighthouse and 

C and D are two ships which make an angle of depression 

with the top A of the lighthouse of 60° and 45°

So, ∠C = 45° and ∠D = 60°

It is given that, AB = 20 m

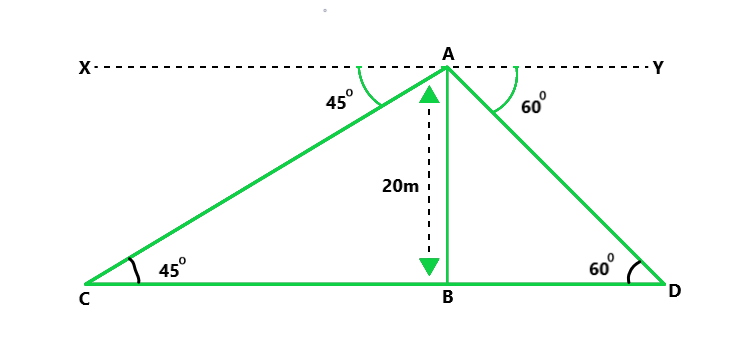
Now in △ACB,

tan 45° = 20/CB

CB = 20m

Similarly, in △ABD,

tan 60° = AB/BD

√3 = 20/BD

BD = 20/√3 = 20√3/3 m

Now, the Distance between two ships

CD = CB + BD

20 + 20/3 √3 = 20(1 + √3)/3 m

= 20 x 0.19 = 18.20m = 18.2m

问题 43. 两极之间的水平距离为 15 m。从第二极的顶部看，第一极的顶部的俯角为30°。如果第二根杆的高度是 24 m，求第一根杆的高度。 (√3 = 1.732)            

解决方案：

Let us considered AB and CD are two poles and 

the distance between them(BD) = 15 m, 

The height of pole(AB) = 24 m 

Angle of elevation from the top of pole CD, to pole AB = 30°

Now, from point C, draw CE || DB

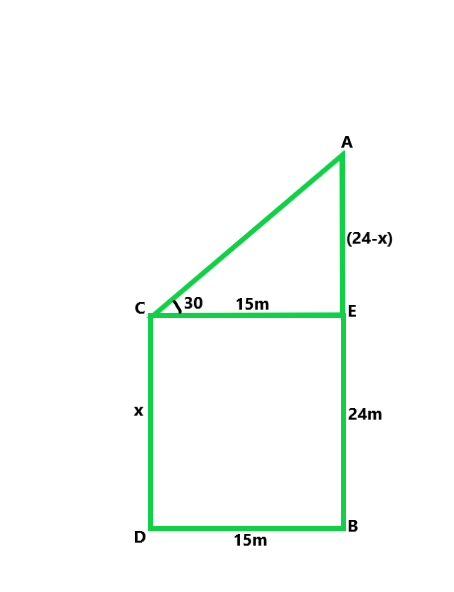
Let us considered CD = x m,

CE = DB = 15m and AE = AB – EB

AE = AB – CD = (24 – x)m

Now in △ACE,

tan 30° = (24 – x)/15

1/√3 = (24 – x)/15

15 = √3 (24 – x)

x = 24 – 15/√3 

Now, after rationalizing we get,

x = 15.34m

问题44 两艘船从灯塔顶部和同侧的俯角分别为45°和30°。如果两艘船相距 200 m，求灯塔的高度。

解决方案：

Let us considered PQ be the lighthouse and 

A and B are two ships on the same side of the lighthouse 

The angle of depression from the top of the lighthouse of the two ships are 30° and 45°

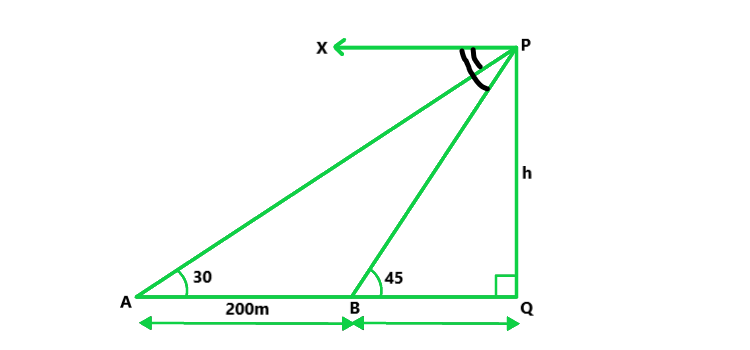
So, ∠A = 30 and ∠b = 45 and AB = 200m

Now, let us considered the height of lighthouse = h,

and BQ = x

Now in △PBQ

tan 45° = h/x 

h = x

Similarly, in △PAQ,

tan 30° = h/(200 + x)

1/√3 = h/(200 + h)

h(√3 – 1) = 200

h = 200/0.732 m = 273.2m

Hence, the height of the house is 273.2m.

问题 45 塔顶从距塔底 4 m 和 9 m 两点的仰角与塔底在同一直线上的仰角互补。证明塔高为6m。

解决方案：

Let us considered TR be the tower. 

A and B are two points which make the angled elevation with top of the tower as θ and 90° – θ (∵ angles are complementary)

Also, the height of tower TR = h and AR = 9 m, BR = 4m

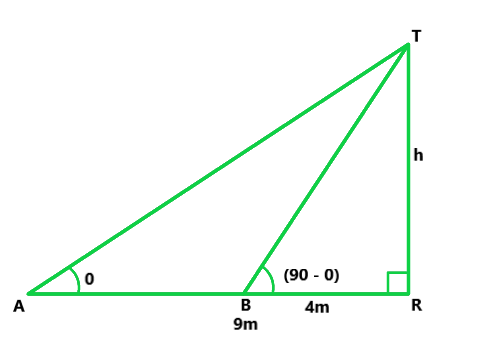
Now in △TAR

tan θ = TR/AR = h/9      ……(i)

Similarly, in right △TBR,

tan(90 – θ) = h/4 = cot θ = h/4    ……(ii)

Now, on multiplying eq(i) and (ii), we get

tan θ x cot θ = h/4 x h/9 

1 = h²/36

h² = 36 

h = 6m

Hence, height of tower is 6m

问题 46. 从 50 m 高的塔顶观察，杆顶和底部的俯角分别为 45° 和 60°。求柱子的高度。

解决方案：

Let us considered AB be the tower and CD is the pole. 

So, the angles of depression from the top A to the top and bottom of the pole are 45° and 60° 

AB = 50 m, 

Let us considered CD = h and BD = EC = x

∵ CE || DB

∴ EB = CD = h

and AE = 50 – h

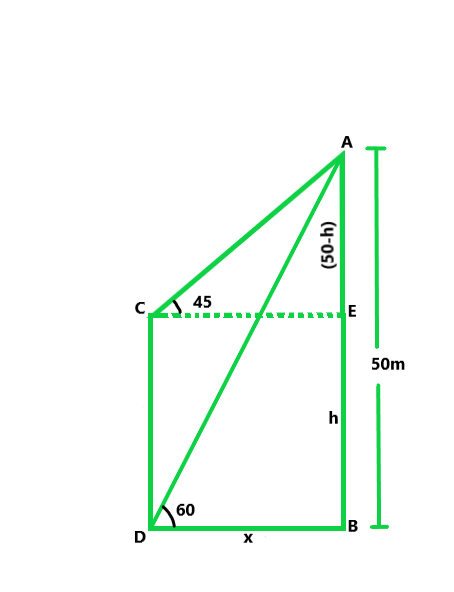
Now in △ADB,

tan 60° = 50/x 

√3 = 50/x

x = 50/√3            ……(i)

Similarly, in △ACE,

tan 45° = AE/CE = 1 = (50 – h)/x

x = 50 – h

x + h = 50

h = 50 – x 

50 – (50/√3) = 21.13m             (using eq(i))

Hence, the height of pole is 21.13m

问题 47. 两棵不同高度的树之间的水平距离为 60 m。当从第二棵树的顶部看时，第一棵树的顶部的俯角为 45°。如果第二棵树的高度是 80 m，求第一棵树的高度。

解决方案：

Let us considered AB and CD be the two trees

So, given that AB = 80 m, angle of depression from A to C is 45°. 

Now, draw CE || DB

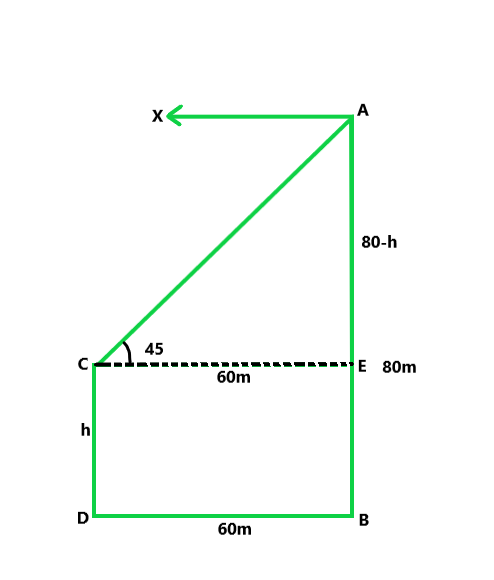
∠ACE = ∠XAC = 45°

Let us assume CD = h

CE = BD = 60 m

EB = CD = h and AE = 80 – h

Now in right △ACE

tan 45° = (80 – h)/60 

80 – h = 60

h = 20m

Hence the height of the second tree is 20m.

问题 48. 一个旗杆站在一座 5 m 高的塔顶上。从地面上的一点看，旗杆顶的仰角为60°，从同一点看，塔顶的仰角为45°。求旗杆的高度。

解决方案：

Let us considered FT is the flag-staff situated on the top of the tower TR. 

Now, A is any point on the same plane that makes elevation angles with 

top of the flag-staff and top of the tower are 60° and 45°.

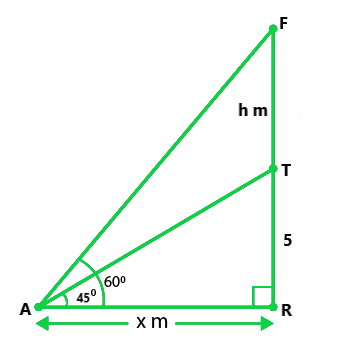
Given that the length of tower TR = 5m

Let us assume that the height of flag-staff FT = h and AR = x, then

In △TAR,

tan 45° = 5/x 

x = 5           …..(i)

Similarly in △FAR,

tan 60° = FR/AR = √3 = (h + 5)/x

x = (h + 5)/√3           ……(ii)

Now, from eq(i) and (ii), we get

5 = (h + 5)/√3

5√3 = h + 5

h = 5(√3 – 1) = 3.65m

Hence the height of the flag-staff is 3.65m.

问题 49. 垂直塔 PQ 顶部从地面 X 点的仰角为 60°。在 X 垂直上方 40 m 的 Y 点，顶部的仰角为 45°。计算塔的高度。

解决方案：

Let us considered that TR is the tower .

Now, from a point X, the angle of elevation of T is 60° and 40 m 

above X, from the point Y, the angle of elevation is 45°

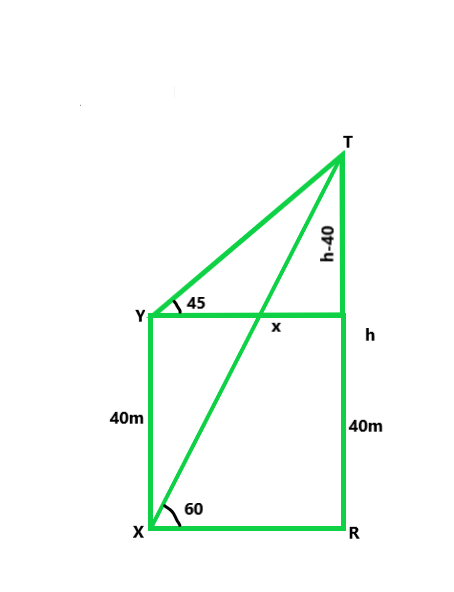
From Y, draw YZ || XR

Let us considered, TR = h and XR = YZ = x

ZR = YX = 40m and TZ = (h – 40) m

In △TXR,

tan 60° = h/x 

√3 = h/x

x = h/√3              ……(i)

Similarly in △TYZ,

tan 45° = TZ/YZ 

1 = (h – 40)/x

x = h – 40              ……(ii) 

From eq(i) and (ii), we get

h/√3 = h – 40

h(√3 – 1) = 40√3

h = 40√3/(√3 – 1)

On rationalize above term and we get,

h = 94.64m

Hence, the height of the tower is 94.64m

问题 50. 从 150 m 高的灯塔顶部观察，接近它的两艘船的俯角分别为 30° 和 45°。如果一艘船就在另一艘船的后面，求两艘船之间的距离。

解决方案：

Let us considered, LH be the lighthouse, 

So, A and B are the two ships making angles of elevation 

with the top of the lighthouse as 30° and 45°.

LH = 150 m.

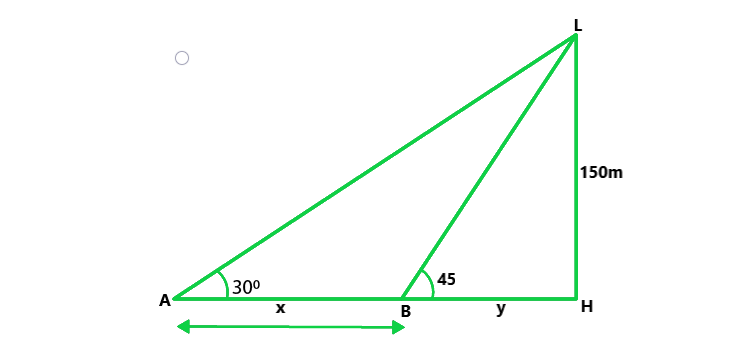
Let us considered AB = x and BH = y

Now in △LAH,

tan 30° = 150/(x + y) 

1/√3 = 150/(x + y)            ……..(i)

Similarly in △LBH,

tan 45° = LH/BH 

1 = 150/y

y = 150  ……(ii)

From eq(i), we get

x + 150 = 150√3

x = 150√3 – 150

= 109.5 m

Hence the Distance between two ships is 109.5 m.

问题51. 100m高的塔顶和脚下岩石顶部的仰角分别为30°和45°。找出岩石的高度。

解决方案：

Let us considered RS is the rock and TP is the tower. 

So, the angles of elevation of the top of the rock with 

the top and foot of the tower are 30° and 45°.

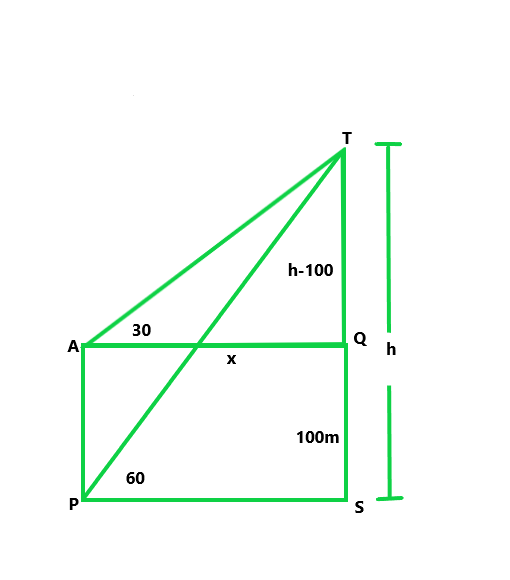
Given that, the height of TP = 100 m

Let the height of rock RS = h

From T, draw TQ || PS                             

Then QS = TP = 100 m                           

and RQ = h – 100

Let us assume, PS = TQ = x

Now in right ΔRPS,

tan 45° = h/x

x = h  …..(i)

Similarly in △RTQ,

tan 30° = RQ/TQ = 1/√3 = (h – 100)/x

x = √3(h – 100)     ….(ii)

From eq(i) and (ii), we get

h = √3(h – 100)

h(√3 – 1) = 100√3

On rationalize above value we get,

h = 50√3(√3 – 1) = 236.5 m

Hence the height of rock is 236.5 m.

问题 52. 一条笔直的公路通向一座 50 m 高的塔脚。从塔顶看，两辆汽车站在高速公路上的俯角分别为30°和60°。两辆车之间的距离是多少，每辆车离塔多远？

解决方案：

Let us considered, TR be the tower 

And A and B are two cars on the road making angles of elevation 

with T the top of the tower as 30° and 60°

Height of the tower TR = 50 m

Let us considered AR = x and BR = y

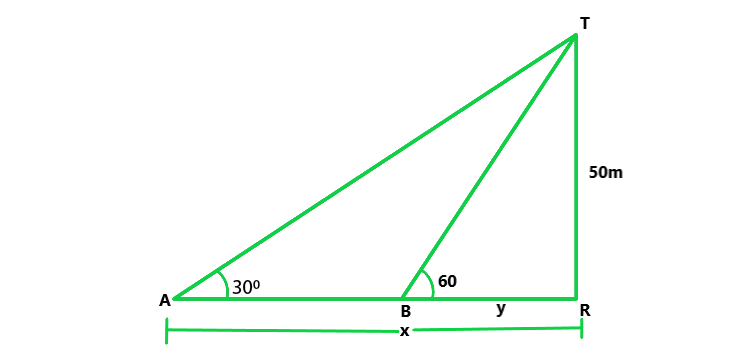
Now in ΔTAR,

tan 30° = TR/AR = 50/x

1/√3 = 50/x

x = 50√3         …….(i)

Similarly in △TRB,

tan 60° = TR/BR = 50/y

√3  =50/y

y = 50/√3       …..(ii)

(i) Now we find the distance between the two cars

AB = AR – BR = x – y

= (50√3 – 50/√3) = 50(√3 – 1/√3)

= 50((3 – 2) / √3) x (50 x 2)/√3

On rationalize above term and we get,

AB = 57.7 m

(ii) Now we find the how far is each car from the tower

Distance of A car = x = 50√3 = 86.65 m

Distance of B car = y = 50/√3 = 50√3/3 = 28.83 m