第 12 类 RD Sharma 解决方案 - 第 6 章行列式 - 练习 6.2 |设置 3
证明下列恒等式:
问题 35。 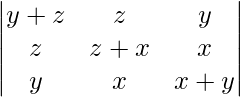 = 4xyz
= 4xyz
解决方案:
Considering the determinant, we have
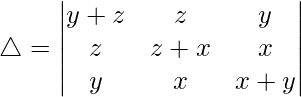
R1⇢R1 – R2 – R3
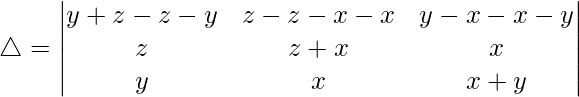
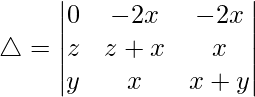
C2⇢C2 – C3
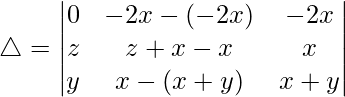
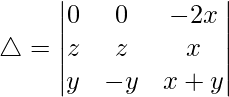
△ = [-2x((z)(-y) – (z)(y))]
△ = [-2x(-zy – zy)]
△ = [-2x(-2zy)]
△ = 4xyz
Hence proved
问题 36。 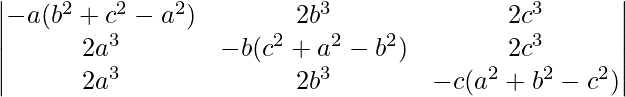 = abc(a 2 + b 2 + c 2 ) 3
= abc(a 2 + b 2 + c 2 ) 3
解决方案:
Considering the determinant, we have
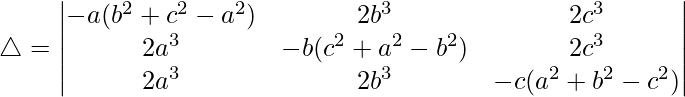
Taking a, b and c common from C1, C2 and C3. We get
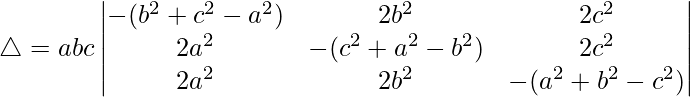
R1⇢R1 – R3 and R2⇢R2 – R3
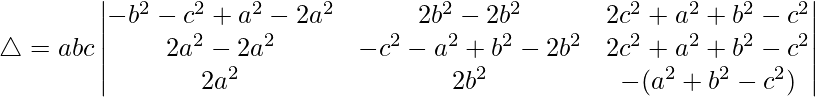

Taking (a2 + b2 + c2) common from R1 and R2, we get
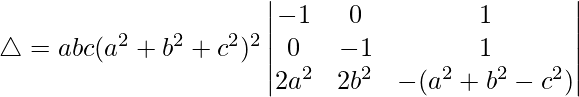
C3⇢C3 + C1
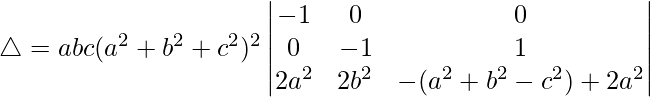
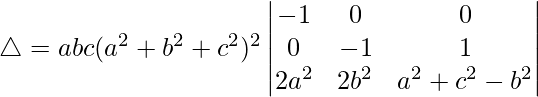
△ = abc(a2 + b2 + c2)2[-1((-1)(a2 + c2 – b2) – (1)(2b2))]
△ = abc(a2 + b2 + c2)2[a2 + c2 – b2 + 2b2]
△ = abc(a2 + b2 + c2)2[a2 + c2 + b2]
△ = abc(a2 + b2 + c2)3
Hence proved
问题 37。 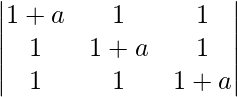 = 一个3 + 3a 2
= 一个3 + 3a 2
解决方案:
Considering the determinant, we have
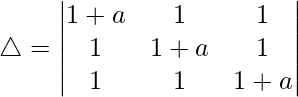
C1⇢C1 + C2 + C3
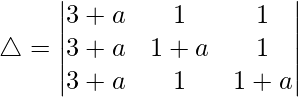
Taking (3 + a) common from C1, we get
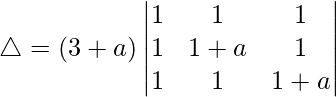
R2⇢R2 – R1 and R3⇢R3 – R1
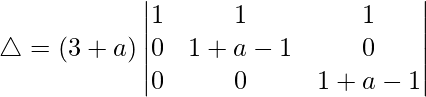
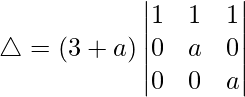
△ = (3 + a)[1((a)(a) – (0)(0))]
△ = (3 + a)[a2]
△ = 3a2 + a3
Hence proved
问题 38。  = (x + y + z)(x – z) 2
= (x + y + z)(x – z) 2
解决方案:
Considering the determinant, we have

R1⇢R1 + R2 + R3
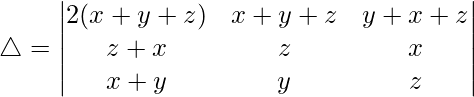
Taking (x + y + z) common from R1, we get
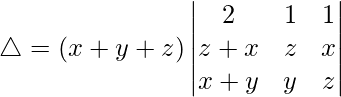
C1⇢C1 – C2 – C3
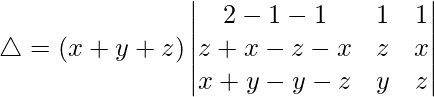
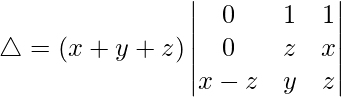
△ = (x + y + z)[(x – z)(x – z)]
△ = (x + y + z)[(x – z)2]
△ = (x + y + z)(x – z)2
Hence proved
问题 39. 不展开,证明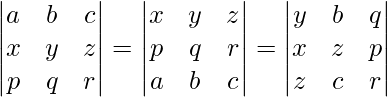
解决方案:
Considering the determinant, we have
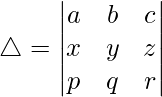
R1↔R2
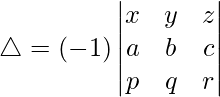
R2↔R3
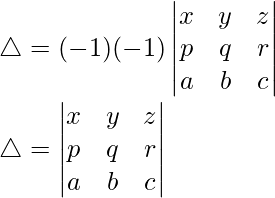
C1↔C2
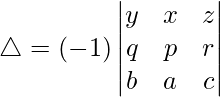
R2↔R3
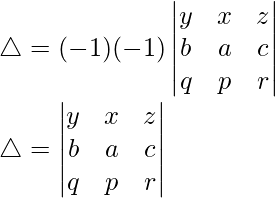
Taking transpose, we have
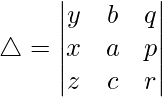
Hence proved
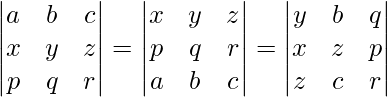
问题 40. 证明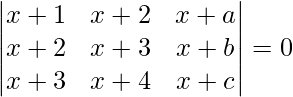 其中 a、b、c 在 AP 中。
其中 a、b、c 在 AP 中。
解决方案:
Considering the determinant, we have
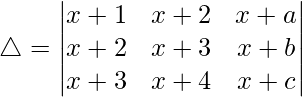
C1⇢C1 + C2 + C3
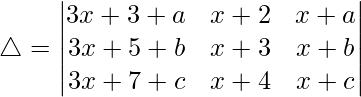
R2⇢R2 – R1 and R3⇢R3 – R2

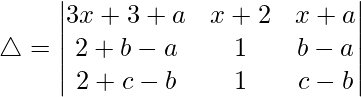
As a, b and c are in AP
then, b – a = c – b = λ
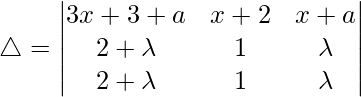
As, R2 and R3 are identical
△ = 0
Hence proved
问题 41. 证明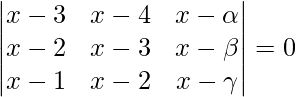 其中 α、β、γ 在 AP 中。
其中 α、β、γ 在 AP 中。
解决方案:
Considering the determinant, we have
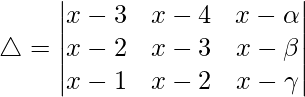
C1⇢C1 + C2 + C3
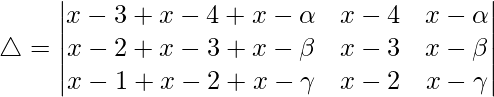

R2⇢R2 – R1 and R3⇢R3 – R2
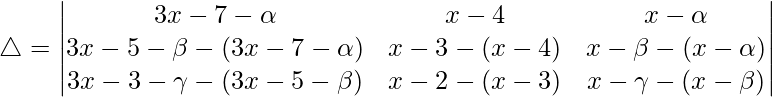
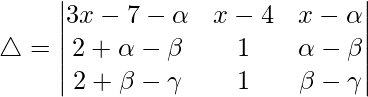
As α, β, γ are in AP
then, β – α = γ – β = λ
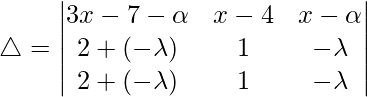
As, R2 and R3 are identical
△ = 0
Hence proved
问题 42. 评估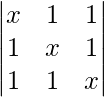
解决方案:
Considering the determinant, we have
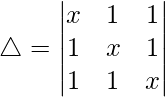
C1⇢C1 + C2 + C3
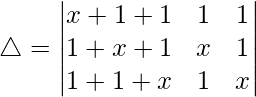
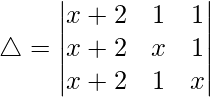
Taking (x + 2) common from C1. we get
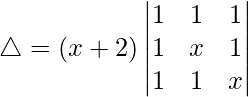
R2⇢R2 – R1 and R3⇢R3 – R2
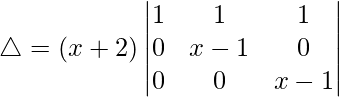
△ = (x + 2)[1((x – 1)(x – 1) – (0)(0))]
△ = (x + 2)(x – 1)2
Hence proved
问题 43. 如果 a、b、c 是实数,使得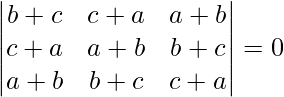 ,然后证明 a + b + c = 0 或 a = b = c。
,然后证明 a + b + c = 0 或 a = b = c。
解决方案:
Considering the determinant, we have
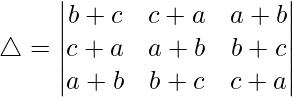
C1⇢C1 + C2 + C3
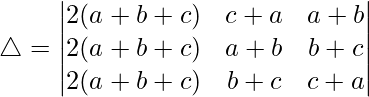
Taking 2(a + b + c) common from C1. We get
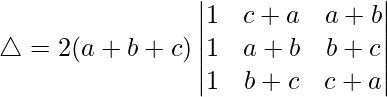
R2⇢R2 – R1 and R3⇢R3 – R2
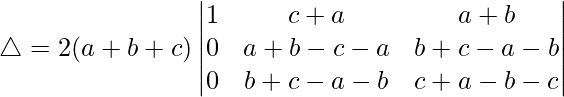
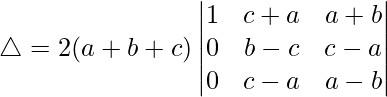
△ = 2(a + b + c)[1((b – c)(a – b) – (c – a)(c – a))]
△ = 2(a + b + c)[ba – b2 – ca + cb – (c – a)2]
△ = 2(a + b + c)[ba – b2 – ca + cb – (c2 + a2 – 2ac)]
△ = 2(a + b + c)[ba – b2 – ca + cb – c2 – a2 + 2ac]
△ = 2(a + b + c)[ba + bc + ac – b2 – c2 – a2]
As, it is given that
△ = 0
2 (a + b + c)(ba + bc + ac – b2 – c2 – a2) = 0
(a + b + c)(ba + bc + ac – b2 – c2 – a2) = 0
So, either (a + b + c) = 0 or (ba + bc + ac – b2 – c2 – a2) = 0
As, ba + bc + ac – b2 – c2 – a2 = 0
On multiplying it by -2, we get
-2ba – 2bc – 2ac + 2b2 + 2c2 + 2a2 = 0
(a – b)2 + (b – c)2 + (c – a)2= 0
As, square power is always positive
(a – b)2 = (b – c)2 = (c – a)2
(a – b) = (b – c) = (c – a)
a = b = c
Hence proved
问题 44. 证明 x=2 是方程的根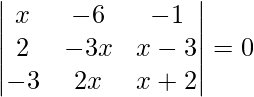 并彻底解决。
并彻底解决。
解决方案:
Considering the determinant, we have
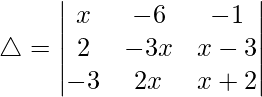
On putting x = 2, we get
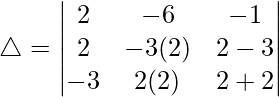
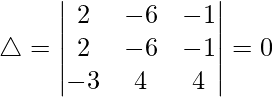
As, R1 = R2
△ = 0
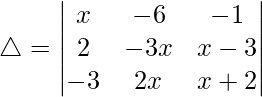
R3⇢R3 – R1
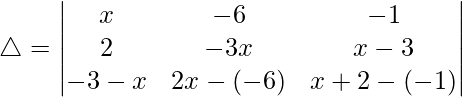
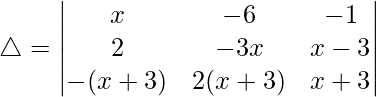
Taking (x + 3) common from R3, we get
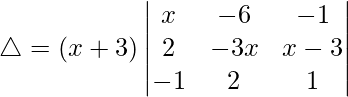
R1⇢R1 – R2
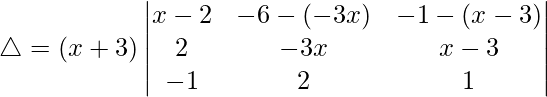
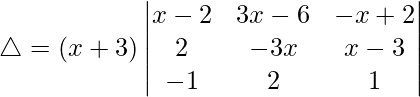
Taking (x – 2) common from R1. We get
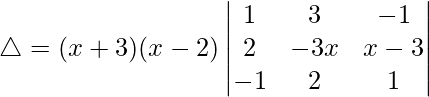
C3⇢C3 + C1
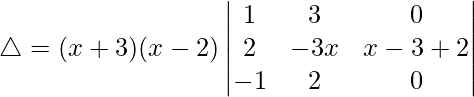
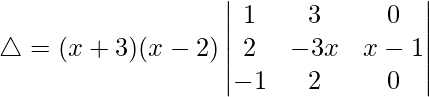
Now, taking (x – 1) common from C3. We get
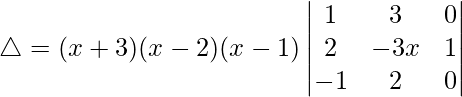
△ = (x + 3)(x – 2)(x – 1)[1((1)(2) – (3)(-1))]
△ = (x + 3)(x – 2)(x – 1)[2 + 3]
△ = 5 (x + 3)(x – 2)(x – 1)
△ = 0
5 (x + 3)(x – 2)(x – 1) = 0
x = 2, 1, -3
问题 45. 求解下列行列式方程:
(一世) 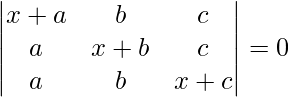
解决方案:
Considering the determinant, we have
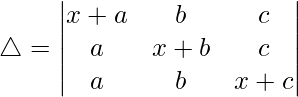
C1⇢C1 + C2 + C3
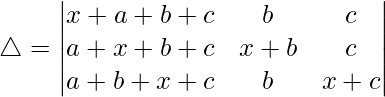
Now, taking (x + a + b + c) common from C1. We get
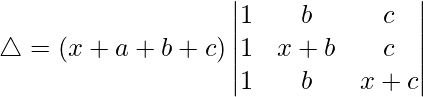
R2⇢R2 – R1 and R3⇢R3 – R1
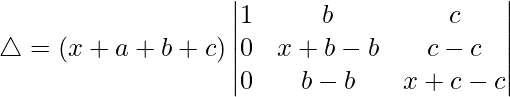
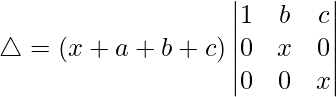
△ = (x + a + b + c)[1((x)(x) – (0)(0))]
△ = (x + a + b + c)[x2]
As △ = 0
(x + a + b + c) x2 = 0
x + a + b + c = 0 or x2 = 0
x = -(a + b + c) or x = 0
(二) 
解决方案:
Considering the determinant, we have
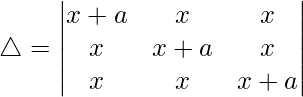
C1⇢C1 + C2 + C3
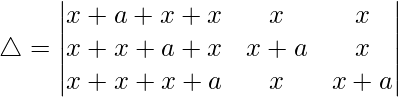
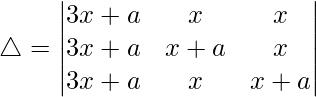
Now, taking (3x + a) common from C1. We get
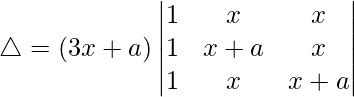
R2⇢R2 – R1 and R3⇢R3 – R1
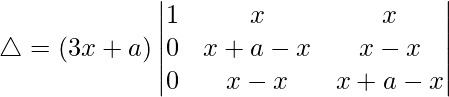
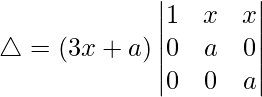
△ = (3x + a)[1((a)(a) – (0)(0))]
△ = (3x + a)[a2]
As △ = 0
(3x + a)[a2] = 0
x = -a/3
㈢ 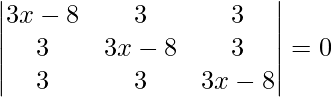
解决方案:
Considering the determinant, we have
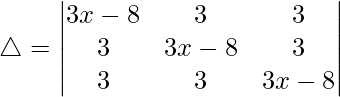
C1⇢C1 + C2 + C3
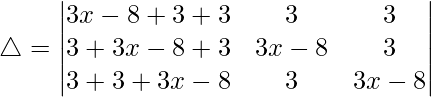
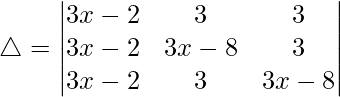
Now, taking (3x – 2) common from C1. We get
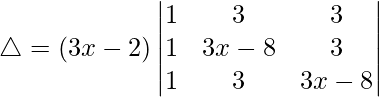
R2⇢R2 – R1 and R3⇢R3 – R1
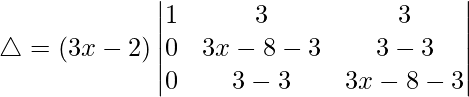
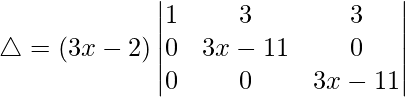
△ = (3x – 2)[1((3x – 11)(3x – 11) – (0)(0))]
△ = (3x – 2)[(3x – 11)2]
As △ = 0
(3x – 2)(3x – 11)2 = 0
3x – 2 = 0 and 3x – 11 = 0
x = 2/3 and x = 11/3
(四) 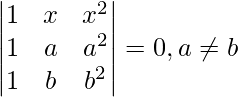
解决方案:
Considering the determinant, we have
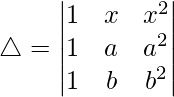
R2⇢R2 – R1 and R3⇢R3 – R1
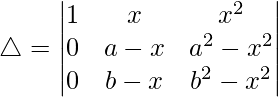
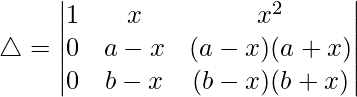
Now, taking (a – x) and (b – x) common from R2 and R3 respectively. We get
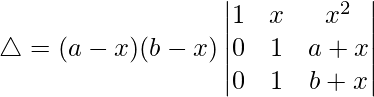
△ = (a – x)(b – x)[1((b + x)(1) – (1)(a + x))]
△ = (a – x)(b – x)[b + x – (a + x)]
△ = (a – x)(b – x)[b + x – a – x]
△ = (a – x)(b – x)[b – a]
As △ = 0
(a – x)(b – x)(b – a) = 0
a – x = 0 and b – x = 0
x = a and x = b
(五) 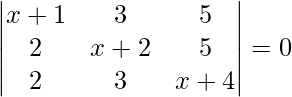
解决方案:
Considering the determinant, we have
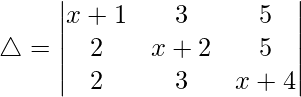
C1⇢C1 + C2 + C3
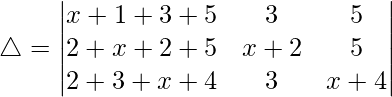
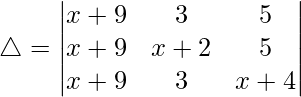
Now, taking (x + 9) common from C1. We get
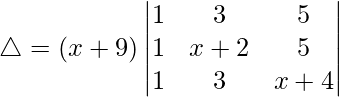
R2⇢R2 – R1 and R3⇢R3 – R1
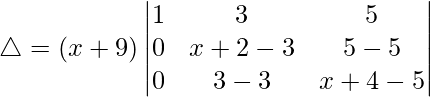
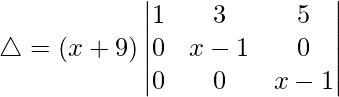
△ = (x + 9)[1((x – 1)(x – 1) – (0)(0))]
△ = (x + 9)(x – 1)2
As △ = 0
(x + 9)(x – 1)2 = 0
x + 9 = 0 or (x – 1)2 = 0
x = -9 or x = 1
(六) 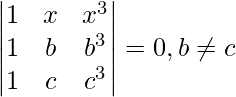
解决方案:
Considering the determinant, we have
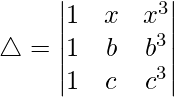
R2⇢R2 – R1 and R3⇢R3 – R1

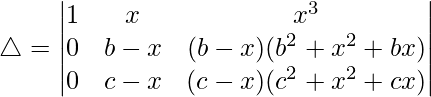
Now, taking (b – x) and (c – x) common from R2 and R3 respectively. We get
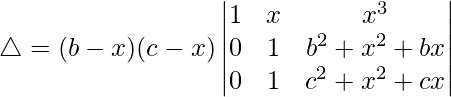
△ = (b – x)(c – x)[1((c2 + x2 + cx)(1) – (b2 + x2 + bx)(1))]
△ = (b – x)(c – x)[(c2 + x2 + cx) – (b2 + x2 + bx)]
△ = (b – x)(c – x)
△ = (b – x)(c – x)
△ = (b – x)(c – x)[(c – b)(c + b) + x(c – b)]
△ = (b – x)(c – x)(c – b)
As △ = 0
(b – x)(c – x)(c – b) = 0
b – x = 0 or c – x = 0 or c – b = 0 or c + b + x = 0
x = b or x = c or c = b or x = -(c + b)
(七) 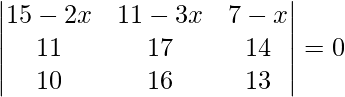
解决方案:
Considering the determinant, we have
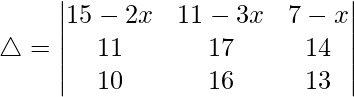
R2⇢R2 – R3
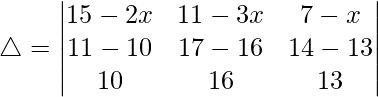
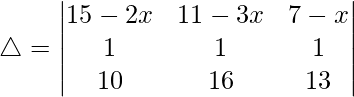
R2⇢R2 – R1 and R1⇢R1 – R3
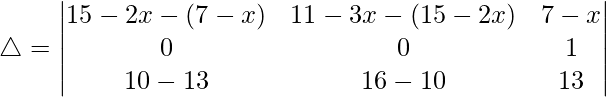
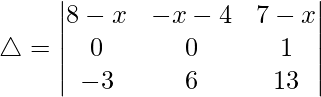
△ = -1[(8 – x)(6) – (-x – 4)(-3)]
△ = -1[(8 – x)(6) – (x + 4)(3)]
△ = [(x + 4)(3) – (8 – x)(6)]
△ = [3x + 12 – (48 – 6x)]
△ = [9x – 36]
As △ = 0
9x – 36 = 0
x = 4
(八) 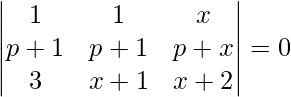
解决方案:
Considering the determinant, we have
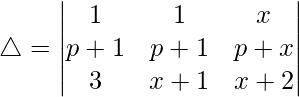
R2⇢R2 – R1
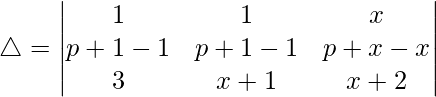
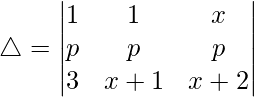
Now, taking p common from R2. We get
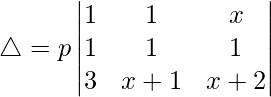
R2⇢R2 – R1
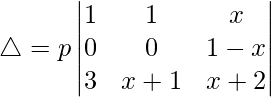
Now, taking 1 – x common from R2. We get
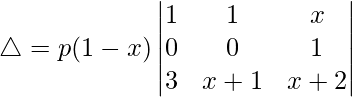
△ = p(1 – x)[-1((x + 1)(1) – (3)(1))]
△ = p(x – 1)[x + 1 – 3]
△ = p(x – 1)[x – 2]
As △ = 0
p(x – 1)(x – 2) = 0
x – 1 = 0 or x – 2 = 0
x = 1 or x = 2