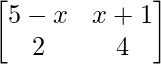第 12 类 RD Sharma 解决方案 - 第 6 章行列式练习前。 6.6 |设置 1

问题 1. 如果 A 是奇异矩阵，则求 |A| 的值。

解决方案：

Given that A is a singular matrix.

So, as we know if A is a n×n matrix and it is singular, the value of its determinant is always 0.

Thus, |A| = 0.

问题 2. 对于 x 的什么值，下面的矩阵是奇异的？

$\begin{bmatrix}5 - x & x + 1 \\ 2 & 4\end{bmatrix}$

解决方案：

Given that 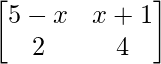$\begin{bmatrix}5 - x & x + 1 \\ 2 & 4\end{bmatrix}$

As we know if A is a n×n matrix and it is singular, so, the value of its determinant is always 0.

=> |A| = 0

=> $\begin{vmatrix}5 - x & x + 1 \\ 2 & 4\end{vmatrix} = 0$

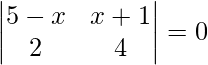
=> 4(5 – x) – 2(x + 1) = 0

=> 20 – 4x – 2x – 2 = 0

=> 18 – 6x = 0

=> 18 = 6x

=> x = 3

Therefore, the value of x is 3.

问题 3. 求行列式的值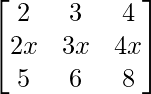$\begin{bmatrix}2 & 3 & 4 \\ 2x & 3x & 4x \\ 5 & 6 & 8\end{bmatrix}$ .

解决方案：

Given that

A = 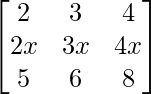$\begin{bma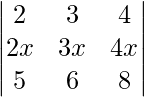trix}2 & 3 & 4 \\ 2x & 3x & 4x \\ 5 & 6 & 8\end{bmatrix}$

|A| = $\begin{vmatrix} 2 & 3 & 4\\ 2x & 3x & 4x \\ 5 & 6 & 8 \end{vmatrix}$

So, on taking out x common from R₂ we get,

|A| = 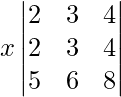$x\begin{vmatrix} 2 & 3 & 4\\ 2 & 3 & 4 \\ 5 & 6 & 8 \end{vmatrix}$

As R₁ = R₂, we get

|A| = 0

Therefore, the value of the determinant is 0.

问题 4. 说明矩阵是否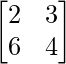$\begin{bmatrix}2 & 3 \\ 6 & 4\end{bmatrix}$是单数或非单数。

解决方案：

Given that

A = 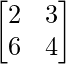$\begin{bmatrix}2 & 3 \\ 6 & 4\end{bmatrix}$

|A| = $\begin{vmatrix}2 & 3 \\ 6 & 4\end{vmatrix}$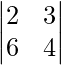

|A| = 2 (4) – 6 (3)

= 8 – 18 

= -10

As we know if A is a n×n matrix and it is singular, so the value of its determinant is always 0.

As |A| = -10 here, the given matrix is non-singular.

问题 5. 找出行列式的值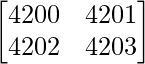$\begin{bmatrix}4200 & 4201 \\ 4202 & 4203\end{bmatrix}$ .

解决方案：

Given that

A = 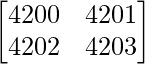$\begin{bma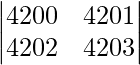trix}4200 & 4201 \\ 4202 & 4203\end{bmatrix}$

|A| = $\begin{vmatrix}4200 & 4201 \\ 4202 & 4203\end{vmatrix}$

On applying C₂ -> C₂ – C₁, we get

|A| = 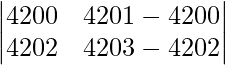$\begin{vmatrix}4200 & 4201-4200 \\ 4202 & 4203-4202\end{vmatrix}$

|A| = $\begin{vmatrix} 4200 & 1\\4202 & 1 \end{vmatrix}$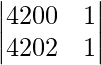

|A| = 4200 – 4202 

|A| = -2

Therefore, the value of determinant is -2.

问题 6. 求行列式的值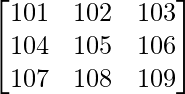$\begin{bmatrix}101 & 102 & 103 \\ 104 & 105 & 106 \\ 107 & 108 & 109\end{bmatrix}$ .

解决方案：

Given that

A = 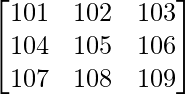$\begin{bma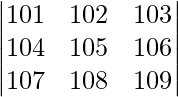trix}101 & 102 & 103 \\ 104 & 105 & 106 \\ 107 & 108 & 109\end{bmatrix}$

|A| = $\begin{vmatrix}101 & 102 & 103 \\ 104 & 105 & 106 \\ 107 & 108 & 109\end{vmatrix}$

On applying C₂ -> C₂ – C₁ and C₃ -> C₃ – C₁, we get

|A| = 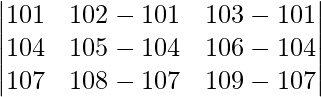$\begin{vmatrix}101 & 102-101 & 103-101 \\ 104 & 105-104 & 106-104 \\ 107 & 108-107 & 109-107\end{vmatrix}$

|A| = $\begin{vmatrix} 101 & 1 & 2\\104 & 1 & 2\\107 & 1 & 2 \end{vmatrix}$

On taking out 2 common from R₃ we get,

|A| = 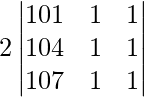$2\begin{vmatrix} 101 & 1 & 1\\104 & 1 & 1\\107 & 1 & 1 \end{vmatrix}$

As R₂ = R₃, we get

|A| = 0

Therefore, the value of the determinant is zero.  

问题 7. 找出行列式的值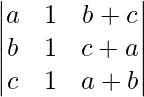$\begin{vmatrix}a & 1 & b + c \\ b & 1 & c + a \\ c & 1 & a + b\end{vmatrix}$ .

解决方案：

Given that

A = 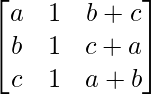$\begin{bma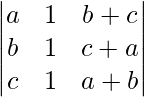trix}a & 1 & b + c \\ b & 1 & c + a \\ c & 1 & a + b\end{bmatrix}$

|A| = $\begin{vmatrix}a & 1 & b + c \\ b & 1 & c + a \\ c & 1 & a + b\end{vmatrix}$

On applying C₁ -> C₁ + C₃ we get,

= $\begin{vmatrix} a + b + c & 1 & b + c\\a + b + c & 1 & c + a\\a + b + c & 1 & a + b \end{vmatrix}$

= $a + b + c \begin{vmatrix} 1 & 1& b + c\\1 & 1 & c + a\\1 & 1 & a + b \end{vmatrix}$

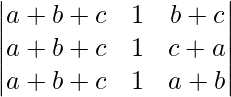
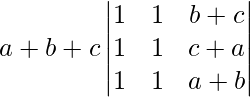
= (a + b + c) (0)

= 0

Therefore, the value of determinant is 0.

问题 8. 如果 A = $\begin{bmatrix}0 & i \\ i & 1\end{bmatrix}$和 B = $\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}$ , 求 |A| 的值+ |B|。

解决方案：

Given that

A = 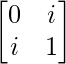$\begin{bma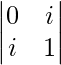trix} 0 & i\\i & 1 \end{bmatrix}$

|A| = $\begin{vmatrix} 0 & i\\i & 1 \end{vmatrix}$

= 0 – i²   

= – (-1)

= 1

Also, we have

B = $\b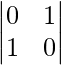egin{bmatrix} 0 & 1\\1 & 0 \end{bmatrix}$

|B| = $\begin{vmatrix} 0 & 1\\1 & 0 \end{vmatrix}$

= 0 – 1 

= -1

So,

|A| + |B| = 1 + (-1) 

= 1 – 1

= 0

Therefore, the value of |A| + |B| is 0.

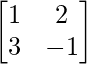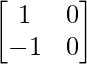问题 9. 如果 A = $\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$和 B = $\begin{bmatrix}1 & 0 \\ - 1 & 0\end{bmatrix}$ , 找到 |AB|。

解决方案：

We have,

A = 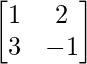$\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$and B =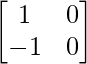 $\begin{bmatrix}1 & 0 \\ - 1 & 0\end{bmatrix}$

So, we get

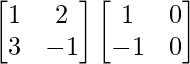
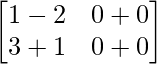
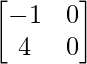
AB = $\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}\begin{bmatrix}1 & 0 \\ - 1 & 0\end{bmatrix}$

= $\begin{bmatrix}1 - 2 & 0 + 0 \\ 3 + 1 & 0 + 0\end{bmatrix}$

= $\begin{bmatrix}- 1 & 0 \\ 4 & 0\end{bmatrix}$

Now we have,

|AB| = $\begin{vmatrix}- 1 & 0 \\ 4 & 0\end{vmatrix}$

= -1 (0) – 0 (4)

= 0 – 0 

= 0

Therefore, the value of |AB| is 0.

问题 10. 评估$\begin{bmatrix}4785 & 4787 \\ 4789 & 4791\end{bmatrix}$ .

解决方案：

Given that

A = 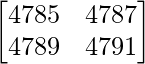$\begin{bma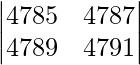trix}4785 & 4787 \\ 4789 & 4791\end{bmatrix}$

|A| = $\begin{vmatrix}4785 & 4787 \\ 4789 & 4791\end{vmatrix}$

On applying C₂ -> C₂ – C₁ we get,

|A| = 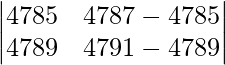$\begin{vmatrix}4785 & 4787-4785 \\ 4789 & 4791-4789\end{vmatrix}$

= $\begin{vmatrix}4785 & 2\\ 4789 & 2\end{vmatrix}$

On taking out 2 common from R₂ we get,

= $2 \times \begin{vmatrix}4785 & 1\\ 4789 & 1\end{vmatrix}$

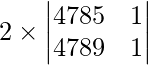
= 2 (4785 – 4789)

= 2 (-4)

= -8

Therefore, the value of the determinant is 0.

问题 11. 如果 w 是一个虚数立方根，求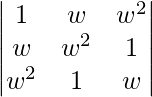$\begin{vmatrix}1 & w & w^2 \\ w & w^2 & 1 \\ w^2 & 1 & w\end{vmatrix}$ .

解决方案：

Given that,

A = 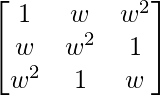$\begin{bma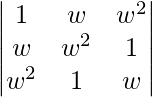trix}1 & w & w^2 \\ w & w^2 & 1 \\ w^2 & 1 & w\end{bmatrix}$

|A| = $\begin{vmatrix}1 & w & w^2 \\ w & w^2 & 1 \\ w^2 & 1 & w\end{vmatrix}$

On applying C₁ -> C₁ + C_{_2} + C_{_3} we get,

= $\begin{vmatrix} 1 + w + w^2 & w & w^2 \\ w + w^2 + 1 & w^2 & 1\\ w^2 + 1 + w & 1 & w \end{vmatrix}$

= $\begin{vmatrix} 0 & w& 7 w^2 \\ 0 & w^2 & 1\\ 0 & 1 & 7 w \end{vmatrix}$

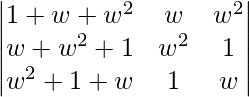
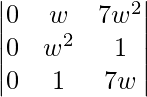
= 0

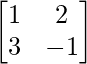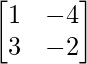问题 12. 如果 A = $\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$和 B = $\begin{bmatrix}1 & - 4 \\ 3 & - 2\end{bmatrix}$ , 找到 |AB|。

解决方案：

Given that

A = 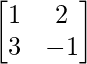$\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$

|A| = -1 – 6 

= -7

B = $\begin{bmatrix}1 & - 4 \\ 3 & - 2\end{bmatrix}$

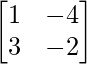
|B| = – 2 + 12 

= 10  

We know if A and B are square matrices of the same order, then we have,

=> |AB| = |A|. |B|

= (-7) (10) 

= -70

Therefore, the value of |AB| is -70.

问题 13. 如果 A = [a _ij ] 是一个 3 × 3 对角矩阵，使得 a ₁₁ = 1, a ₂₂ = 2 a ₃₃ = 3，则求 |A|。

解决方案：

Given that  a₁₁ = 1, a₂₂ = 2 and a₃₃ = 3.

If A is a diagonal matrix of order n x n, then we have

=> $\left| A \right| = a_{11} \times a_{22} \times a_{33} \times . . . \times a_{nn}$

So, we get

|A| = 1 (2) (3)

= 6 

Therefore, the value of |A| is 6.

问题 14. 如果 A = [a _ij ] 是一个 3 × 3 标量矩阵，使得 a ₁₁ = 2，则求 |A| 的值。

解决方案：

Given that A = [a_ij] which is a 3 × 3 scalar matrix and a₁₁ = 2,

As we know that a scalar matrix is a diagonal matrix, in which all the diagonal elements are equal to a given scalar number.

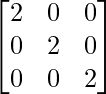
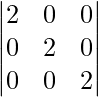
=> A = $\begin{bmatrix} 2 & 0 & 0\\0 & 2 & 0\\0 & 0 & 2 \end{bmatrix}$

= $\begin{vmatrix} 2 & 0 & 0\\0 & 2 & 0\\ 0 & 0 & 2 \end{vmatrix}$

On expanding along C₁, we get

= $2 \times \begin{vmatrix} 2 & 0\\ 0 & 2 \end{vmatrix}$

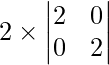
= 2 (2) (2)

= 8

Therefore, the value of |A| is 8.

问题 15. 如果 I ₃表示一个 3 × 3 阶单位矩阵，求其行列式的值。

解决方案：

As we know that in an identity matrix, all the diagonal elements are 1 and the remaining elements are 0.

Here,

I₃ = 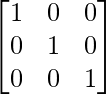$\begin{bmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1 \end{bmatrix}$

= $\begin{vmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1 \end{vmatrix}$

On expanding along C₁, we get

= $1 \times \begin{vmatrix} 1 & 0\\0 & 1 \end{vmatrix}$

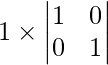
= 1

Therefore, the value of the determinant is 1.

问题 16. 3 × 3 阶矩阵 A 的行列式为 5。|3A| 的值是多少？

解决方案：

Given that matrix A is of order 3 x 3 and the determinant = 5.

If A is a square matrix of order n and k is a constant, then we have

=> |kA| = kⁿ |A|

Here,  

Number of rows = n  

Also, k is a common factor from each row of k.

Hence, we get

3A = 3³ |A|

= 27 (5)

= 135

Therefore, the value of |3A| is 135.

问题 17. 由第一行展开，3 × 3 方阵 A = [a _ij ] 的行列式值为 a ₁₁ C ₁₁ + a ₁₂ C ₁₂ + a ₁₃ C ₁₃ ，其中 [C _ij ] 是A 中_ij的辅因子。写出它的值的表达式，以扩展第二列。

解决方案：

As we know that if a square matrix(let say  A) is of order n, then the sum of the products of elements of a row or a column with their cofactors is always equal to det (A). 

So, 

$\sum^n_{i = 1} a_{i j} C_{i j} = \left| A \right|$

Also, $\sum^n_{j = 1} a_{i j} C_{i j} = \left| A \right|$

On expanding along R₁ we get,

|A| = a₁₁ C₁₁ + a₁₂ C₁₂ + a₁₃ C₁₃

Now,  

On expanding along C₂ we get,

|A| = a₁₂ C₁₂ + a₂₂ C₂₂ + a₃₂ C₃₂

问题 18. 由第一行展开，3 × 3 方阵 A = [a _ij ] 的行列式值为 a ₁₁ C ₁₁ + a ₁₂ C ₁₂ + a ₁₃ C ₁₃ ，其中 [C _ij ] 是A 中_ij的辅因子。写出它的值的表达式，以扩展第二列。

解决方案：

As we know that if a square matrix(let say  A) is of order n, then the sum of the products of elements of a row or a column with their cofactors is always equal to det (A). 

So, 

$\sum^n_{i = 1} a_{i j} C_{i j} = \left| A \right|$

Also, $\sum^n_{j = 1} a_{i j} C_{i j} = \left| A \right|$

On expanding along R₁ we get,

|A| = a₁₁ C₁₁ + a₁₂ C₁₂ + a₁₃ C₁₃

Now,  

On expanding along C₂ we get,

|A| = a₁₂ C₁₂ + a₂₂ C₂₂ + a₃₂ C₃₂ = 5