第 12 类 RD Sharma 解决方案 - 第 6 章行列式 - 练习 6.2 |设置 1
问题 1. 评估以下决定因素:
(一世) 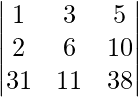
解决方案:
Considering the determinant, we have
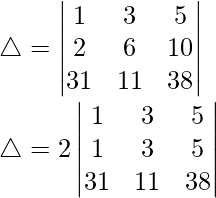
As R1 and R2 are identical
Hence, △ = 0
(二) 
解决方案:
Considering the determinant, we have

C1⇢C1 – 3C3
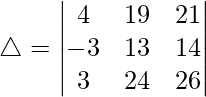
R3⇢R3 + R2 and R1⇢R1 + R2
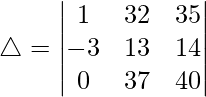
R2⇢R2 + 3R1

△ = 1(109 × 40 – 119 × 37)
Hence, △ = -43
㈢ 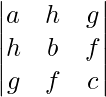
解决方案:
Considering the determinant, we have
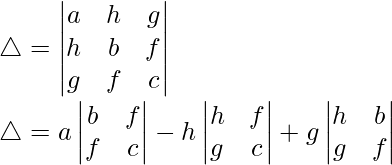
△ = a(bc – f2) – h(hc – fg) + g(hf – gb)
△ = abc – af2 – h2c + fgh + fgh – g2b
Hence, △ = abc + 2fgh – af2 – ch2 – bg2
(四) 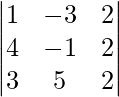
解决方案:
Considering the determinant, we have
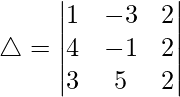
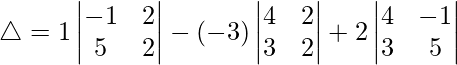
△ = 1(-2 – 10) + 3(8 – 6) + 2(20 + 3)
△ = 1(-12) + 3(2) + 2(23)
△ = -12 + 6 + 46
Hence, △ = 40
(五) 
解决方案:
Considering the determinant, we have
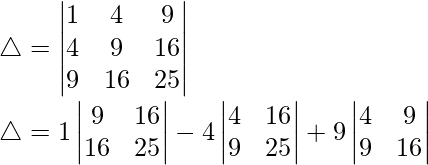
△ = 1(225-256) + 4(100-144) + 9(64-81)
△ = 1(-31) – 4(-44) + 9(-17)
△ = -31 + 176 – 153
Hence, △ = -8
(六) 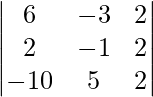
解决方案:
Considering the determinant, we have
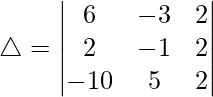
Taking -2 common from C1, C2 and C3
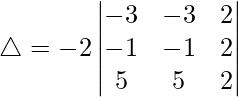
As C1 and C2 are identical
Hence, △ = 0
(七) 
解决方案:
Considering the determinant, we have

C1⇢C1 + C2 + C3
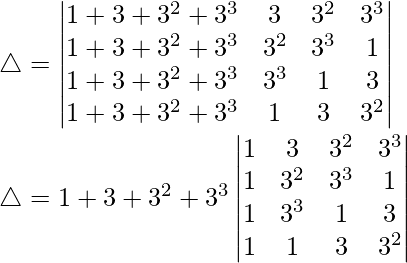
C2⇢C2 – C1
C3⇢C3 – C1
C4⇢C4 – C1
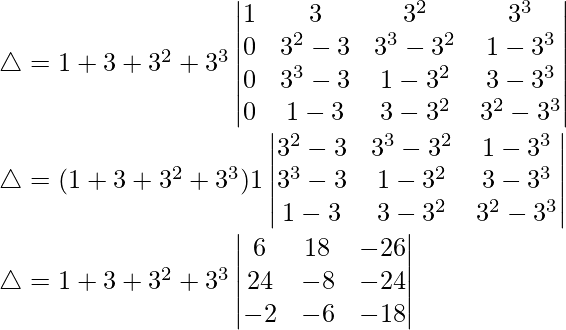
Taking 2, -2 and -2 common from C1, C2 and C3
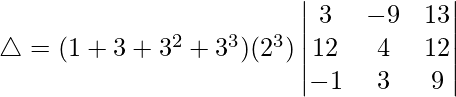
Taking 4 common from R2 and R1⇢R1+3R3
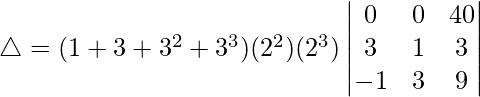
△ = (1 + 3 + 32 + 33)(4)(8)[40(9 – (-1))]
△ = (40)(4)(8)[40(9 + 1)]
△ = 40 × 4 × 8 × 40 × 10
Hence, △ = 512000
(八) 
解决方案:
Considering the determinant, we have
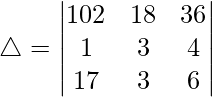
Taking 6 common from R1, we get
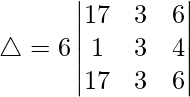
As R1 and R3 are identical
Hence, △ = 0
问题 2. 在不展开的情况下,证明以下每个行列式的值都为零:
(一世) 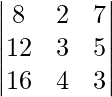
解决方案:
Considering the determinant, we have
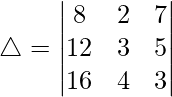
Taking 4 common from C1, we get
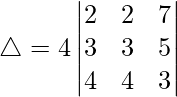
As C1 and C2 are identical
Hence, △ = 0
(二) 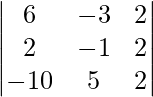
解决方案:
Considering the determinant, we have
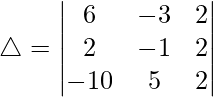
Taking -2 common from C1, we get
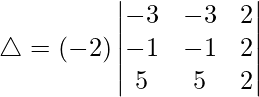
As C1 and C2 are identical
Hence, △ = 0
㈢ 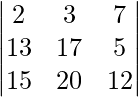
解决方案:
Considering the determinant, we have

R3⇢R3 – R2
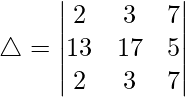
As R1 and R3 are identical
Hence, △ = 0
(四) 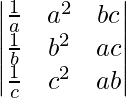
解决方案:
Considering the determinant, we have

Multiplying and dividing △ by abc, we get
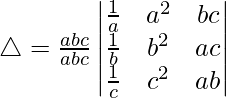
Multiplying R1, R2 and R3 by a, b and c respectively
Taking abc common from C3, we get
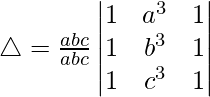
As C2 and C3 are identical
Hence, △ = 0
(五) 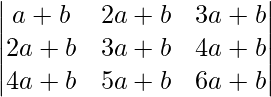
解决方案:
Considering the determinant, we have
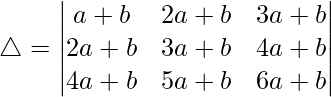
C3⇢C3 – C2 and C2⇢C2 – C1
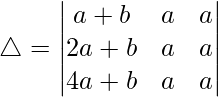
As C2 and C3 are identical
Hence, △ = 0
(六) 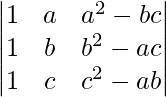
解决方案:
Considering the determinant, we have
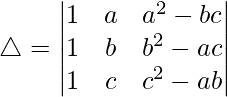
Splitting the determinant, we have
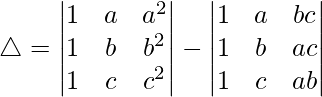
R2⇢R2-R1 and R3⇢R3-R1
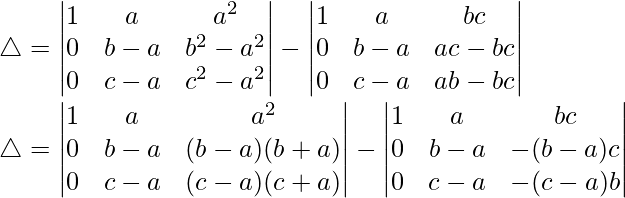
Taking (b-a) and (c-a) common from R2 and R3, we have
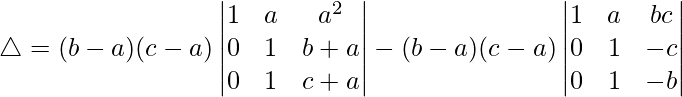
△ = (b – a)(c – a)(c + a – (b + a)) – (b – a)(c – a)(-b – (-c))
△ = (b – a)(c – a)(c + a – b – a) – (b – a)(c – a)(-b + c)
△ = (b – a)(c – a)(c – b) – (b – a)(c – a)(c – b)
Hence, △ = 0
(七) 
解决方案:
Considering the determinant, we have
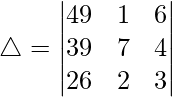
C1⇢C1 – 8C3
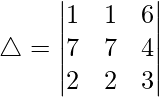
As C1 and C2 are identical
Hence, △ = 0
(八) 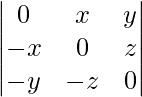
解决方案:
Considering the determinant, we have
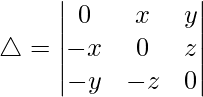
Multiplying and dividing by xyz, we have
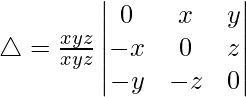
Multiplying C1, C2 and C3 by z, y and x respectively
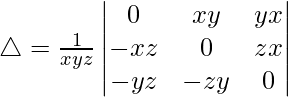
Taking y, x and z common in R1, R2 and R3 respectively
C2⇢C2 – C3
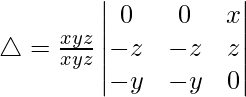
As C1 and C2 are identical
Hence, △ = 0
(九) 
解决方案:
Considering the determinant, we have
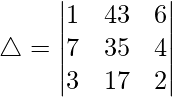
C2⇢C2 – 7C3
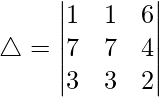
As C1 and C2 are identical
Hence, △ = 0
(X) 
解决方案:
Considering the determinant, we have

C3⇢C3 – C2 and C4⇢C4 – C1

Taking 3 common from C3, we get

As C3 and C4 are identical
Hence, △ = 0
(十一) 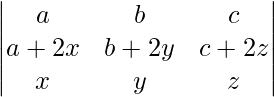
解决方案:
Considering the determinant, we have
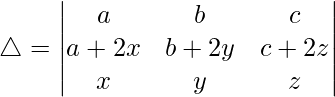
R3⇢R3 + R1 and R2⇢R2 + R1
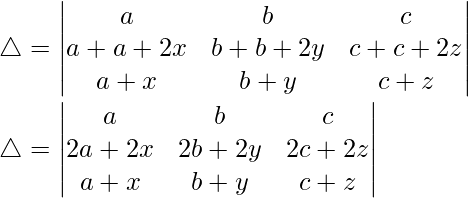
Taking 2 common from R2, we get
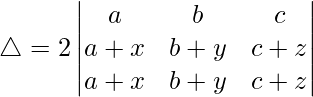
As R2 and R3 are identical
Hence, △ = 0
问题 3。 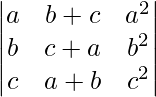
解决方案:
Considering the determinant, we have
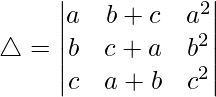
C2⇢C2+C1
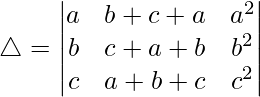
Taking (a+b+c) common from C2, we get
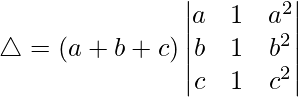
R3⇢R3-R1 and R2⇢R2-R1
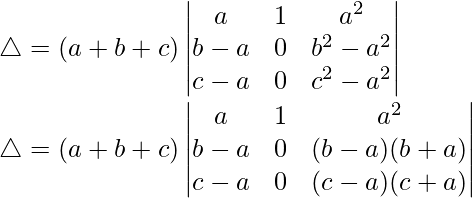
Taking (b – a) and (c – a) from R2 and R3, we have
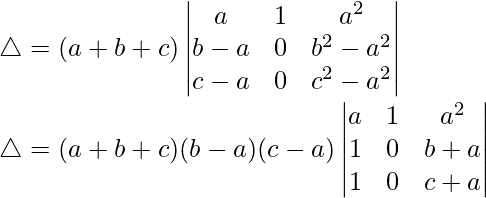
△ = (a + b + c)(b – a)(c – a)[1(b + a – (c + a))]
△ = (a + b + c)(b – a)(c – a)(b + a – c – a)
Hence, △ = (a + b + c)(b – a)(c – a)(b – c)
问题 4。 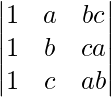
解决方案:
Considering the determinant, we have
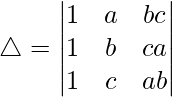
R3⇢R3-R1 and R2⇢R2-R1
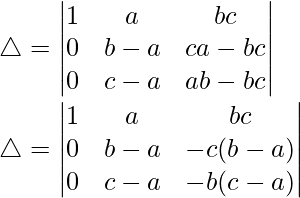
Taking (b-a) and (c-a) from R2 and R3, we have
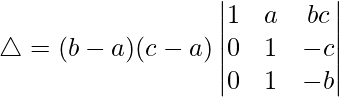
△ = (b – a)(c – a)[1((1)(-b) – (1)(-c))]
△ = (b – a)(c – a)[-b – (-c)]
△ = (b – a)(c – a)[-b + c]
Hence, △ = (a – b)(b – c)(c – a)
问题 5。 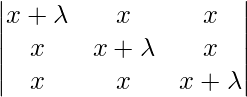
解决方案:
Considering the determinant, we have
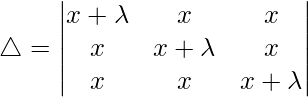
C1⇢C1+C2+C3
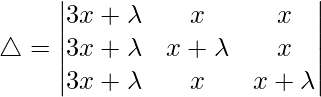
Taking (3x+λ) common from C1, we get
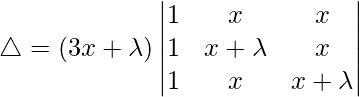
R3⇢R3-R1 and R2⇢R2-R1
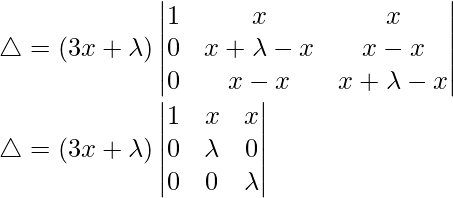
△ = (3x + λ)[λ(λ(1) – 0)]
△ = (3x + λ)[λ(λ)]
Hence, △ = λ2(3x + λ)
问题 6。 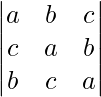
解决方案:
Considering the determinant, we have
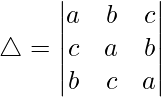
C1⇢C1 + C2 + C3
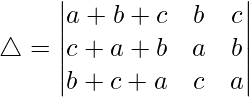
Taking (a + b + c) common from C1, we get
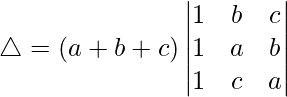
R3⇢R3 – R1 and R2⇢R2 – R1
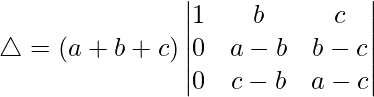
△ = (a + b + c)[1((a – b)(a – c) – (c – b)(b – c))]
△ = (a + b + c)[(a2 – ac – ab + bc) – (cb – c2 – b2 + bc)]
△ = (a + b + c)[a2 – ac – ab + bc + c2 + b2 – 2bc]
Henfce, △ = (a + b + c)[a2 + b2 + c2 – ac – ab – bc]
问题 7。 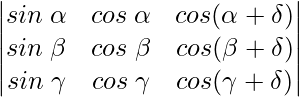
解决方案:
Considering the determinant, we have
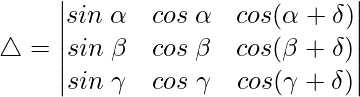
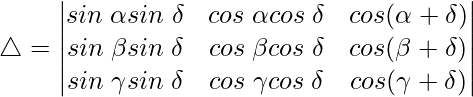
C2⇢C2 – C1
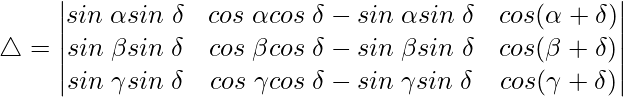
Using the trigonometric identity,
cos a cos b – sin a sin b = cos (a + b)
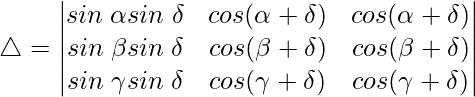
As C2 and C3 are identical
Hence, △ = 0
证明下列恒等式:
问题 8。 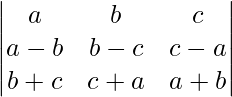 = a 3 + b 2 + c 3 – 3abc
= a 3 + b 2 + c 3 – 3abc
解决方案:
Considering the determinant, we have
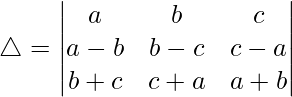
R3⇢R3 + R1 and R2⇢R2 + R1
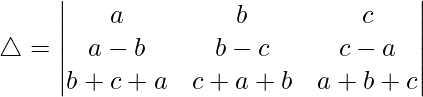
Taking (a + b + c) common from R3, we get
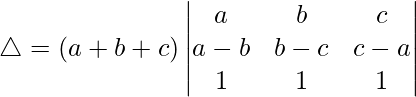
R2⇢R2 – R1
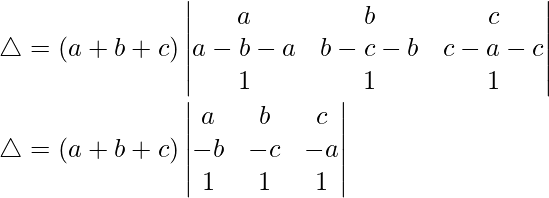
Taking (-1) common from R2, we get
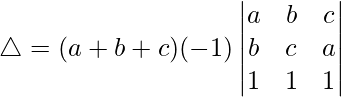
C1⇢C1 – C2 and C2⇢C2 – C3
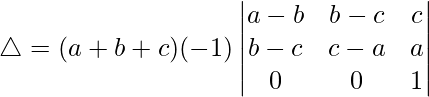
△ = (-1)(a + b + c)[1((a – b)(c – a) – (b – c)(b – c))]
△ = (-1)(a + b + c)[(a – b)(c – a) – (b – c)2]
△ = (-1)(a + b + c)[(ac – a2 – bc + ab) – (b2 – 2cb + c2)]
△ = (-1)(a + b + c)(ac – a2 – bc + ab – b2 + 2cb – c2)
△ = (a + b + c)(-ac + a2 – bc – ab + b2 + c2)
△ = (a + b + c)(a2 + b2 + c2 – ac – ab – cb)
△ = a3 + b3 + c3 – 3abc
Hence proved
问题 9。 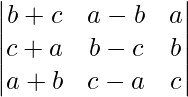 = 3abc – a 3 – b 2 – c 3
= 3abc – a 3 – b 2 – c 3
解决方案:
Considering the determinant, we have
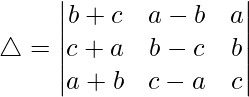
C1⇢C1 + C3
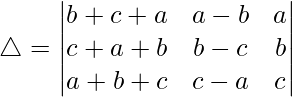
Taking (a + b + c) common from C1, we get
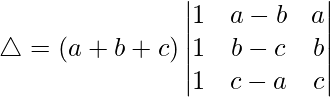
△ = (a + b + c)[1((b – c)c – b(c – a)) – 1((a – b)c – a(c – a)) + 1(b(a – b) – a(b – c))]
△ = (a + b + c)[(b – c)c – b(c – a) – (a – b)c + a(c – a) + b(a – b) – a(b – c)]
△ = (a + b + c)[(bc – c2-bc + ab) – (ac – bc) + ac – a2 + ab – b2 – (ab – ac)]
△ = (a + b + c)[bc – c2 – bc + ab – ac + bc + ac – a2 + ab – b2 – ab + ac]
△ = (a + b + c)[bc – c2 + ab + ac – a2 – b2]
△ = (a + b + c)[bc + ab + ac – a2 – b2 – c2]
△ = 3abc – a3 – b3 – c3
Hence proved
问题 10。 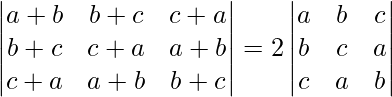
解决方案:
Considering the determinant, we have
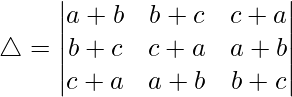
C1⇢C1 + C2 + C3
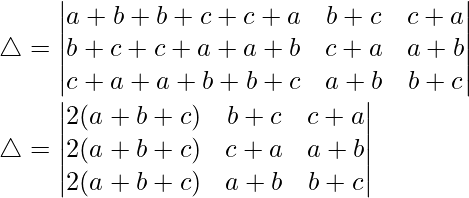
Taking 2 common from C1, we get
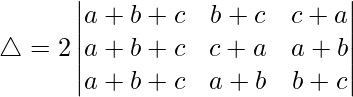
C2⇢C2 – C1 and C3⇢C3 – C1
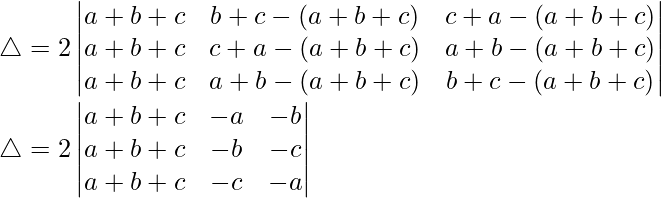
Taking (-1) and (-1) common from C2 and C3,
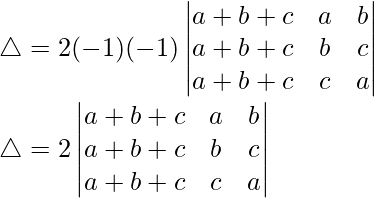
By splitting the determinant, we get
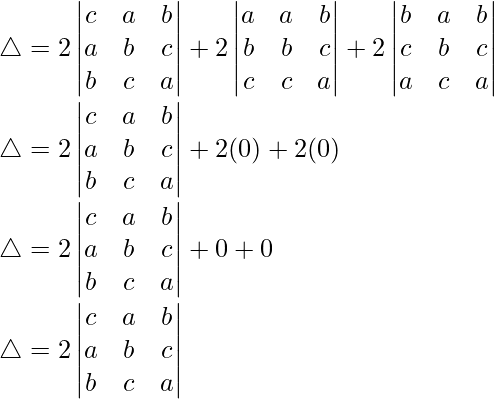
Hence proved
问题 11。 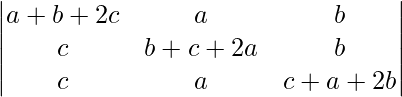 = 2(a + b + c) 3
= 2(a + b + c) 3
Considering the determinant, we have
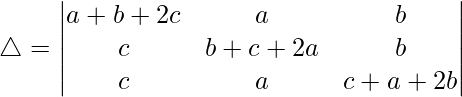
C1⇢C1 + C2 + C3
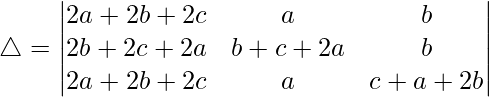
Taking (2a + 2b + 2c) common from C1, we get
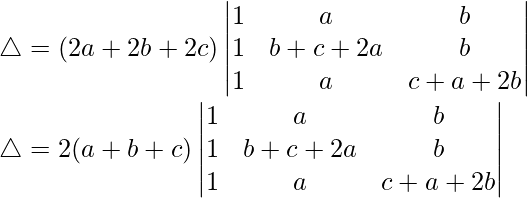
R2⇢R2 – R1 and R3⇢R3 – R1
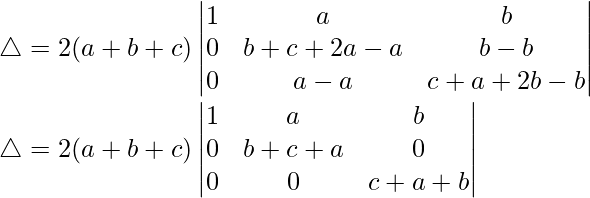
△ = 2(a + b + c)[1((a + b + b)(a + b + c) – 0)]
△ = 2(a + b + c)[(a + b + b)2]
△ = 2(a + b + c)3
Hence proved
问题 12。 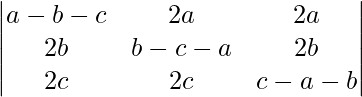 = (a + b + c) 3
= (a + b + c) 3
解决方案:
Considering the determinant, we have

R1⇢R1 + R2 + R3
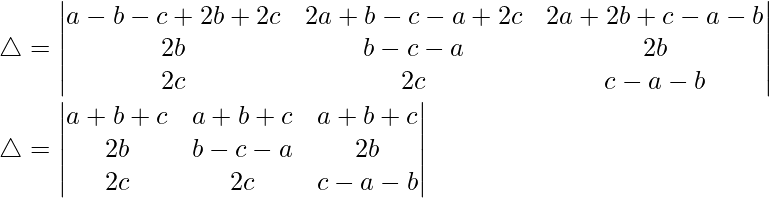
Taking (a + b + c) common from R1, we get
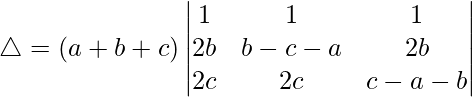
C2⇢C2 – C1 and C3⇢C3 – C1
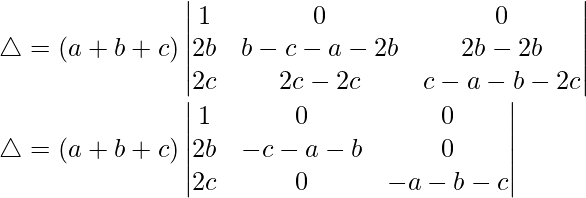
△ = (a + b + c)[1((-b – c – a)(-b – c – a) – 0)]
△ = (a + b + c)[(b + c + a)(b + c + a)]
△ = (a + b + c)[(b + c + a)2]
△ = (a + b + c)3
Hence proved
问题 13。 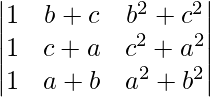 = (a – b)(b – c)(c – a)
= (a – b)(b – c)(c – a)
解决方案:
Considering the determinant, we have
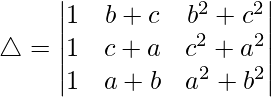
R2⇢R2 – R1 and R3⇢R3 – R1
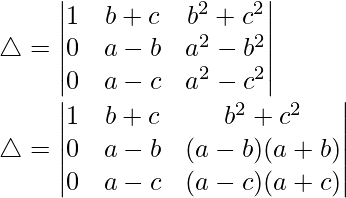
Taking (a – b) and (a – c) common from R2 and R3 respectively, we get
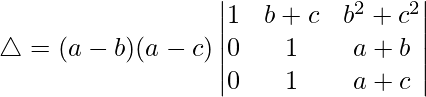
△ = (a – b)(a – c)[1(1(a + c) – 1(a + b))]
△ = (a – b)(a – c)[(a + c) – (a + b)]
△ = (a – b)(a – c)[a + c – a – b]
△ = (a – b)(a – c)
△ = (a – b)(a – c)(c – b)
△ = (a – b)(b – c)(c – a)
Hence proved
问题 14。 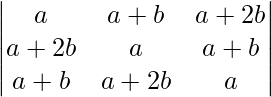 = 9(a + b)b 2
= 9(a + b)b 2
解决方案:
Considering the determinant, we have
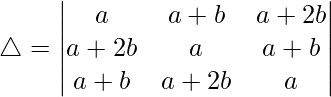
C1⇢C1 + C2 + C3
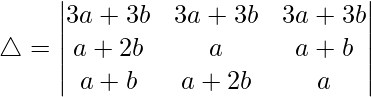
Taking (3a + 3b) common from R1, we get
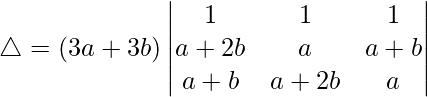
C2⇢C2 – C1 and C3⇢C3 – C2
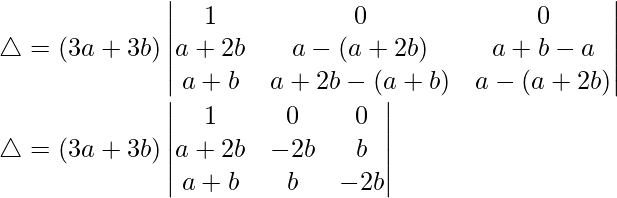
△ = 3(a + b)[1((-2b)(-2b) – b(b))]
△ = 3(a + b)[4b2 – b2]
△ = 3(a + b)[3b2]
△ = 9(a + b)b2
Hence proved
问题 15。 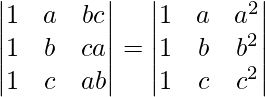
解决方案:
Considering the determinant, we have
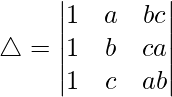
R1⇢aR1, R2⇢bR2 and R3⇢cR3
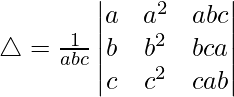
Taking (abc) common from C3, we get
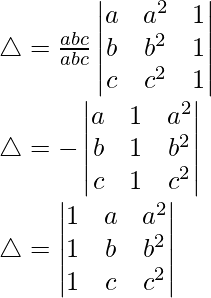
Hence proved
问题 16。 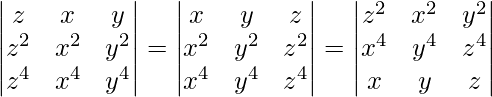 = xyz(x – y)(y – z)(z – x)(x + y + z)
= xyz(x – y)(y – z)(z – x)(x + y + z)
解决方案:
Considering the determinant, we have
C1↔C2 and then
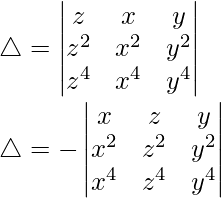
C2↔C3
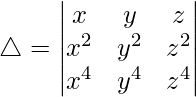
R1↔R2
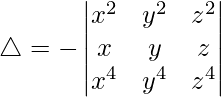
R2↔R3
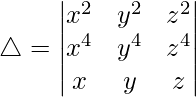
Taking,
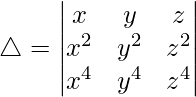
Taking x, y and z common from C1, C2 and C3 respectively
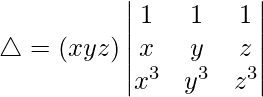
C1⇢C1 – C2 and C3⇢C3 – C2
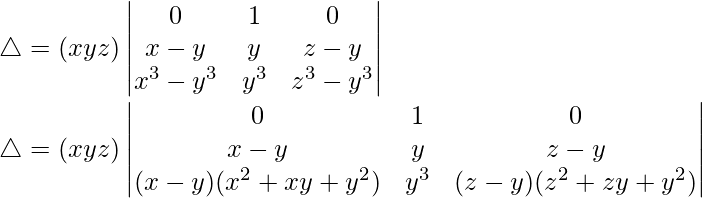
Taking (x – y) and (z – y) common from C1 and C3 respectively, we get
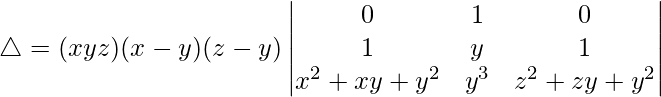
△ = (xyz)(x – y)(z – y)[1(1(z2 + zy + y2) – 1(x2 + xy + y2))]
△ = (xyz)(x – y)(z – y)[z2 + zy + y2 – (x2 + xy + y2)]
△ = (xyz)(x – y)(z – y)[z2 + zy + y2 – x2 – xy – y2]
△ = (xyz)(x – y)(z – y)[z2 + zy – x2 – xy]
△ = (xyz)(x – y)(z – y)[z2 – x2 + zy – xy]
△ = (xyz)(x – y)(z – y)[(z – x)(z + x) + y(z – x)]
△ = (xyz)(x – y)(z – y)(z – x)[z + x + y]
△ = (xyz)(x – y)(z – y)(z – x)(x + y + z)
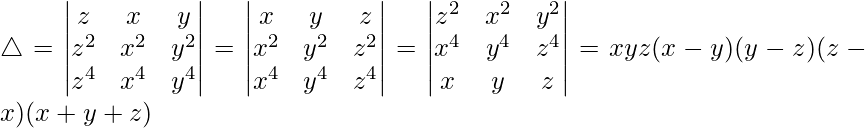
Hence proved
问题 17。 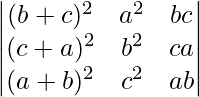 = (a – b)(b – c)(c – a)(a + b + c)(a 2 + b 2 + c 2 )
= (a – b)(b – c)(c – a)(a + b + c)(a 2 + b 2 + c 2 )
解决方案:
Considering the determinant, we have
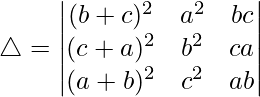
C1⇢C1 + C2 – 2C3
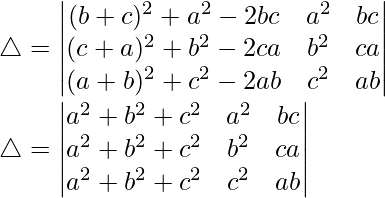
Taking (a2 + b2 + c2) common from C1, we get
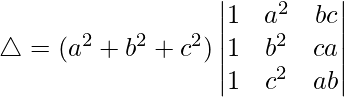
C2⇢C2-C1 and C3⇢C3-C1
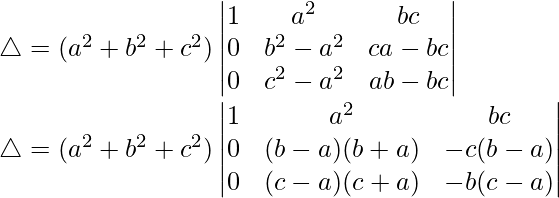
Taking (b – a) and (c – a) common from R2 and R3, we get
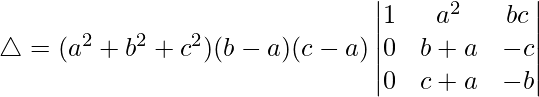
△ = (a2 + b2 + c2)(b – a)(c – a)[1((b + a)(-b) – (c + a)(-c))]
△ = (a2 + b2 + c2)(b – a)(c – a)[(b + a)(-b) + (c + a)c]
△ = (a2 + b2 + c2)(b – a)(c – a)[(-b2 – ab) + (c2 + ac)]
△ = (a2 + b2 + c2)(b – a)(c – a)
△ = (a2 + b2 + c2)(b – a)(c – a)[(c – b)(c + b) + a(c – b)]
△ = (a2 + b2 + c2)(b – a)(c – a)(c – b)
△ = (a2 + b2 + c2)(a + b + c)(a – b)(b – c)(c – a)
Hence proved