第 12 类 RD Sharma 解决方案 - 第 22 章微分方程 - 练习 22.1 |设置 1
确定下列微分方程的阶和阶。还要说明它是线性的还是非线性的(问题 1-13)
问题 1。 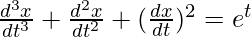
解决方案:
We have,
![]()
Order of function:
The Highest order of derivative of function is 3 i.e.,![]()
So, the order of derivative is equal to 3.
Degree of function:
As the power of the highest order derivative of function is 1 (i.e., power of ![]() is 1)
is 1)
So, degree of function is 1.
Linear or Non-linear:
The given equation is non-linear.
问题2。 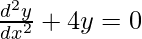
解决方案:
We have,
![]()
Order of function:
As the highest order of derivative of function is 2.(i.e.,![]() )
)
So, Order of the function is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 1(i.e., power of ![]() is 1)
is 1)
So, Degree of the function is equal to 1.
Linear or Non-linear:
The given equation is linear.
问题 3。 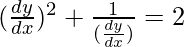
解决方案:
We have,
![]()
![]()
![]()
Order of function:
As the highest order of derivative of function is 1 (i.e., ![]() )
)
So, Order of the function is equal to 1.
Degree of function
As the power of the highest order derivative of the function is 3 (i.e., power of dy/dx is 3)
So, the degree of the function is equal to 3.
Linear or Non-linear:
The given equation is non-linear.
问题 4。 ![由 QuickLaTeX.com 渲染 \sqrt{[1+(\frac{dy}{dx})^2]} =(c\frac{d^2y}{dx^2})^\frac{1}{3}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions-_Chapter_22_Differential_Equations_%E2%80%93_Exercise_22.1_%7C_Set_1_13.jpg)
解决方案:
We have,
![]()
On squaring both side, we get
![]()
On cubing both side, we get
![]()
![]()
Order of function:
As the highest order of derivative of function is 2 (i.e.,![]()
So, Order of the function is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 2. (i.e., power of ![]() is 2)
is 2)
So, the Degree of the function is equal to 2.
Linear or Non-linear:
The given equation is non-linear.
问题 5。 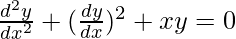
解决方案:
We have,
![]()
Order of function:
As the highest order of derivative of function is 2
So, Order of the function is equal to 2.
Degree of function:
As the power of the highest order derivative of function is 1 (i.e., power of ![]() is 1)
is 1)
So, the Degree of the function is equal to 1.
Linear or Non-linear:
The given equation is non-linear.
问题 6。 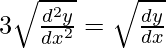
解决方案:
We have,
![]()
On cubing both side, we get
![]()
On squaring both side, we get
![]()
Order of function:
As the highest order of derivative of function is 2 (i.e., ![]() )
)
So, the Order of the function is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 2(i.e., power of ![]() is 2)
is 2)
So, the Degree of the function is equal to 2.
Linear or Non-linear:
The given equation is non-linear.
问题 7。 ![由 QuickLaTeX.com 渲染 \frac{d^4y}{dx^4}=[c+(\frac{dx}{dy})^2]^\frac{3}{2}](https://mangodoc.oss-cn-beijing.aliyuncs.com/geek8geeks/Class_12_RD_Sharma_Solutions-_Chapter_22_Differential_Equations_%E2%80%93_Exercise_22.1_%7C_Set_1_29.jpg)
解决方案:
We have,
![]()
On squaring both side, we get
![]()
![]()
![]()
Order of function:
The highest order of derivative of function is 4 (i.e., ![]() )
)
So, the order of the derivative is equal to 4.
Degree of function:
As the power of the highest order derivative of the function is 2 (i.e., power of ![]() is 2)
is 2)
So, the degree of function is 2.
Linear or Non-linear:
The given equation is non-linear.
问题 8: 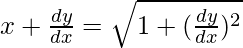
解决方案:
We have,
![]()
On squaring both side, we have
![]()
![]()
![]()
![]()
Order of function:
As the highest order of derivative of function is 1.
So, the Order of the function is equal to 1.
Degree of function:
As the power of the highest order derivative of the function is 1.
So, the degree of the function is equal to 1.
Linear or Non-linear:
The given equation is linear.
问题 9: 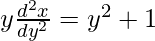
解决方案:
We have,
![]()
![]()
Order of function:
As the highest order of derivative of function is 2 (i.e.,![]() )
)
So, order of derivative is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 1 (i.e., power of ![]() is 1)
is 1)
So, the Degree of the function is equal to 1.
Linear or Non-linear:
The given equation is linear.
问题 10: 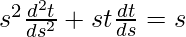
解决方案:
We have,
![]()
Order of function:
As the highest order of derivative of the function is 2.
So, the Order of the function is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 1 (i.e., power of ![]() is 1)
is 1)
So, the Degree of the function is equal to 1.
Linear or Non-linear:
The given equation is non-linear.
问题 11: 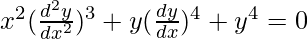
解决方案:
We have,
![]()
Order of function:
As the highest order of derivative of the function is 2
So, the Order of the function is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 3. (i.e., power of ![]() is 3)
is 3)
So, the degree of the function is equal to 3.
Linear or Non-linear:
The given equation is non-linear.
问题 12: 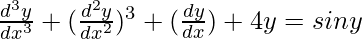
解决方案:
We have,
![]()
Order of function:
As the highest order of derivative of the function is 3
So, the Order of the function is equal to 3.
Degree of function:
As the power of the highest order derivative of the function is 1.(i.e., power of ![]() is 1)
is 1)
So, the Degree of the function is equal to 1.
Linear or Non-linear:
The given equation is non-linear.
问题 13: 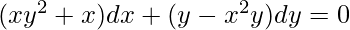
解决方案:
We have,
![]()
![]()
![]()
Order of function:
As the highest order of derivative of the function is 1
So, the Order of the function is equal to 1.
Degree of function:
As the power of the highest order derivative of the function is 1. (i.e., power of dy/dx is 1)
So, the Order of the function is equal to 1.
Linear or Non-linear:
The given equation is non-linear.