第 11 课 RD Sharma 解决方案-第 23 章直线-练习 23.16

问题1.确定以下一对平行线之间的距离：

(i) 4x – 3y – 9 = 0 和 4x – 3y – 24 = 0

(ii) 8x + 15y – 34 = 0 和 8x + 15y + 31 = 0

(iii) y = mx + c 和 y = mx + d

(iv) 4x + 3y – 11 = 0 和 8x + 6y = 15

解决方案：

(i) 4x – 3y – 9 = 0 and 4x – 3y – 24 = 0

Given:

The parallel lines are

4x − 3y − 9 = 0 —(Equation-1)

4x − 3y − 24 = 0 —(Equation-2)

Let ‘d’ be the distance between the given lines.

Thus,

d = 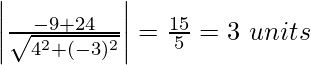$\left|\frac{-9+24}{\sqrt{4^2+(-3)^2}}\right|=\frac{15}{5}=3\ units$

Therefore, 

The distance between givens parallel line is 3 units.

(ii) 8x + 15y – 34 = 0 and 8x + 15y + 31 = 0

Given:

The parallel lines are

8x + 15y − 34 = 0 —(Equation-1)

8x + 15y + 31 = 0 —(Equation-2)

Let ‘d’ be the distance between the given lines.

Thus,

d = $\left|\frac{-34-31}{\sqrt{8^2+15^2}}\right|=\frac{65}{17}\ units$

Therefore,

The distance between givens parallel line is $\frac{65}{17}$ units.

(iii) y = mx + c and y = mx + d

Distance between y = mx + c and y = mx + d is

$\left|\frac{c-d}{\sqrt{m^2+1}}\right|$

(iv) 4x + 3y – 11 = 0 and 8x + 6y = 15

The distance between 4x + 3y – 11 = 0 and 8x + 6y = 15 is

$\left|\frac{-11-15}{\sqrt{4^2+3^2}}\right|=\frac{7}{10}\ units$

问题 2. 正方形两侧的方程是 5x – 12y – 65 = 0 和 5x – 12y + 26 = 0。求正方形的面积。

解决方案：

Given:

Two side of square are 5x – 12y – 65 = 0 and 5x – 12y + 26 = 0

The sides of a square are

5x − 12y − 65 = 0 —(Equation-1)

5x − 12y + 26 = 0 —(Equation-2)

Here we can see that lines (1) and (2) are parallel.

Hence, the distance between them will give the length of the side of the square.

Let ‘d’ be the distance between the given lines.

d = $\left|\frac{-65-26}{\sqrt{5^2+(-12)^2}}\right|=\frac{91}{13}=7$

Therefore, 

Area of the square = 7² = 49 square units

问题 3. 求两条平行于 x + 7y + 2 = 0 且距点 (1, -1) 单位距离的直线的方程。

解决方案：

Given:

The equation is parallel to x + 7y + 2 = 0 and at unit distance from the point (1, -1)

The equation of given line is

x + 7y + 2 = 0 —(Equation-1)

The equation of a line parallel to line x + 7y + 2 = 0 is given below:

x + 7y + λ = 0 —(Equation-2)

The line x + 7y + λ = 0 is at a unit distance from the point (1, − 1).

Thus,

1 = $\left|\frac{1-7+λ}{\sqrt{1+49}}\right|$

λ – 6 = ± 5√2

λ = 6 + 5√2, 6 – 5√2

Now, 

Substitute the value of λ back in equation x + 7y + λ = 0, we get

x + 7y + 6 + 5√2 = 0 and x + 7y + 6 – 5√2

Therefore, The required lines:

x + 7y + 6 + 5√2 = 0 and x + 7y + 6 – 5√2

问题 4. 证明线 2x + 3y = 19 和 2x + 3y + 7 = 0 与线 2x + 3y = 6 等距。

解决方案：

Given:

The lines A, 2x + 3y = 19 and B, 2x + 3y + 7 = 0 also a line C, 2x + 3y = 6.

Let d₁ be the distance between lines 2x + 3y = 19 and 2x + 3y = 6,

While d₂ is the distance between lines 2x + 3y + 7 = 0 and 2x + 3y = 6

d₁ =$\left|\frac{-19-(-6)}{\sqrt{2^2+3^2}}\right|$ and d₂ = $\left|\frac{7-(-6)}{\sqrt{2^2+3^2}}\right|$

d₁ = $\left|-\frac{13}{\sqrt{13}}\right|=\sqrt{13}$ and d₂ = $\left|\frac{13}{\sqrt{13}}\right|=\sqrt{13}$

Hence, proved, the lines 2x + 3y = 19 and 2x + 3y + 7 = 0 are equidistant from the line 2x + 3y = 6

问题 5. 求平行线 9x + 6y – 7 = 0 和 3x + 2y + 6 = 0 之间的直线方程。

解决方案：

Given:

9x + 6y – 7 = 0 and 3x + 2y + 6 = 0 are parallel lines

The given equations of the lines are shown as:

3x + 2y – $\frac{7}{3}$ = 0 —(Equation-1)

3x + 2y + 6 = 0 —(Equation-2)

Let the equation of the line midway between the parallel lines (1) and (2) be

3x + 2y + λ = 0 —(Equation-3)

The distance between (1) and (3) and the distance between (2) and (3) are equal.

$\left|\frac{-\frac{7}{3}-λ}{\sqrt{3^2+2^2}}\right|=\left|\frac{6-λ}{\sqrt{3^2+2^2}}\right|\\ \left|-λ +\frac{7}{3}\right|=|6-λ |$

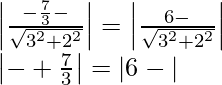
6 – λ = λ + $\frac{7}{3}$

λ = $\frac{11}{6}$

Now substitute the value of λ back in equation 3x + 2y + λ = 0, we get

3x + 2y + $\frac{11}{6}$ = 0

By taking LCM

18x + 12y + 11 = 0

Therefore, 

The required equation of line is 18x + 12y + 11 = 0.

问题 6. 求直线 3x + 4y + 2 = 0 与直线 3x + 4y + 5 = 0 和 3x + 4y – 5 = 0 之间的距离的比值。

解决方案：

Clearly, the slope of each of the given lines is same equal to $-\frac{3}{4}$

Hence, the line 3x + 4y + 2 = 0 is parallel to each of the given lines.

Putting y = 0 in 3x + 4y + 2 = 0, we get x = $-\frac{2}{3}$

So, the coordinates of a point on 3x + 4y + 2 = 0 are \$\left(-\frac{2}{3},0\right)$

The distance d₁ between the lines 3x + 4y + 2 = 0 and 3x + 4y + 5 = 0 is given by

d₁ = 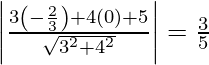$\left|\frac{3\left(-\frac{2}{3}\right)+4(0)+5}{\sqrt{3^2+4^2}}\right|=\frac{3}{5}$

The distance d₂ between the lines 3x + 4y + 2 = 0 and 3x + 4y – 5 =0 is given by

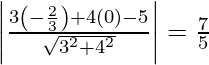
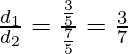
d₂ = $\left|\frac{3\left(-\frac{2}{3}\right)+4(0)-5}{\sqrt{3^2+4^2}}\right|=\frac{7}{5}$

$\frac{d_1}{d_2}=\frac{\frac{3}{5}}{\frac{7}{5}}=\frac{3}{7}$

So, 3x + 4y + 2 = 0 divides the distance between the lines 3x + 4y + 5 = 0 and 3x + 4y – 5 = 0 in the ratio 3 : 7.