类别10 NCERT解决方案-第3章两个变量的线性方程对–练习3.4

问题1.用消除法和替换法求解下面的线性方程对：

(i)x + y = 5和2x – 3y = 4

解决方案：

Here, the two given eqn. are as follows:

x + y = 5 ……….(I)

2x – 3y = 4 ………..(II)

ELIMINATION METHOD:

Multiply equation (I) by 2, and then subtract (II) from it, we get

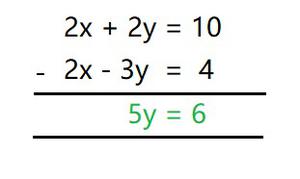
5y = 6

y = 6/5

Now putting y=6/5 in eqn. (I), we get

x + 6/5 = 5

x = (5–(6/5))

x = 19/5

SUBSTITUTION METHOD:

From (I), we get

y=5–x…….(III)

Now substituting the value of y in eqn. (II), we get

2x – 3(5–x) = 4 

2x – 15+3x = 4 

5x = 4+15

x = 19/5

As, putting x = 19/5, in eqn. (III), we get

y = 5 – 19/5

y = 6/5

Hence, by elimination method and substitution method we get,

x = 19/5 and y = 6/5.

(ii)3x + 4y = 10和2x – 2y = 2

解决方案：

Here, the two given eqn. are as follows:

3x + 4y = 10 ……….(I)

2x – 2y = 2 ………..(II)

ELIMINATION METHOD:

Multiply equation (II) by 2, and then add it to (I), we get

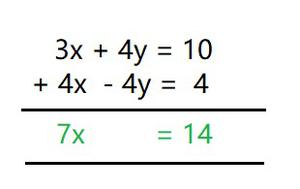
7x = 14

x = 14/7 

x = 2

Now putting x = 2 in eqn. (I), we get

3(2) + 4y = 10

4y = 10 – 6

y = 4/4

y = 1

SUBSTITUTION METHOD:

From (II), we get

x = (2+2y)/2 

x = y+1 …….(III)

Now substituting the value of x in eqn. (I), we get

3(y+1) + 4y = 10

3y + 3 + 4y = 10

7y = 10 – 3

y = 7/7

y = 1

As, putting y = 1, in eqn. (III), we get

x = 1+1

x = 2

Hence, by elimination method and substitution method we get,

x = 2 and y = 1.

(iii)3x – 5y – 4 = 0和9x = 2y + 7

解决方案：

Here, the two given eqn. are as follows:

3x – 5y – 4 = 0

9x = 2y + 7

By rearranging we get,

3x – 5y = 4 ……….(I)

9x – 2y = 7 ………..(II)

ELIMINATION METHOD:

Multiply equation (I) by 3, and then subtract (II) from it, we get

–13y = 5

y = -5/13

Now putting y = – 5/13 in eqn. (I), we get

3x – 5(– 5/13) = 4

3x  = 4 – (25/13)

3x = 27/13

x = 9/13

SUBSTITUTION METHOD:

From (I), we get

3x – 5y = 4

x = (4+5y)/3 …….(III)

Now substituting the value of x in eqn. (II), we get

9((4+5y)/3) – 2y = 7

3(4+5y) – 2y = 7

12+15y – 2y = 7

13y = – 5

y = – 5/13

As, putting y = – 5/13, in eqn. (III), we get

x=(4+5(– 5/13))/3

x = 9/13

Hence, by elimination method and substitution method we get,

x=9/13 and y=– 5/13.

(iv)x / 2 + 2y / 3 = -1和x – y / 3 = 3

解决方案：

Here, the two given eqn. are as follows:

x/2 + 2y/3 = –1 ………..(A)

x – y/3 = 3 ……………….(B)

by rearranging (multiply (A) by 6 and multiply (B) by 3) we get,

3x + 4y = – 6 ……….(I)

3x – y = 9  ………..(II)

ELIMINATION METHOD:

Subtract (II) from (I), we get

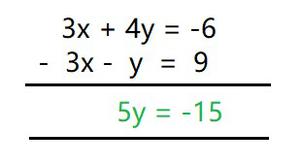
5y = – 15

y = – 3

Now putting y = -3 in eqn. (II), we get

3x – (– 3) = 9 

3x = 9 – 3

x = 6/3

x = 2

SUBSTITUTION METHOD:

From (II), we get

3x – y = 9

y = 3x – 9 …….(III)

Now substituting the value of y in eqn. (I), we get

3x + 4(3x – 9) = – 6 

3x + 12x – 36 = – 6 

15x = – 6 + 36

x = 30/15

x = 2

As, putting x = 2, in eqn. (III), we get

y = 3(2) – 9

y = – 3

Hence, by elimination method and substitution method we get,

x=2 and y=– 3.

问题2.在以下问题中形成一对线性方程，并通过消除方法找到它们的解(如果存在)：

(i)如果我们在分子上加1并从分母中减去1，那么分数将减少为1。如果我们仅将1加到分母，则分数变为½。分数是多少?

解决方案：

Let the fraction be p/q, where p is numerator and q is denominator.

Here, According to the given condition,

(p+1)/(q – 1) = 1 ………………..(A)

and,

p/(q+1) = 1/2 …………………..(B)

Solving (A), we get

(p+1) = q – 1

p – q = – 2 ……………………….(I)

Now, solving (B), we get

2p = (q+1)

2p – q = 1 ……………………….(II)

When equation (I) is subtracted from equation (II) we get,

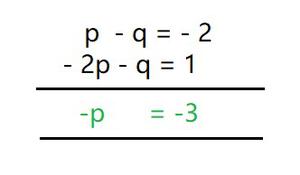
p = 3

Now putting p = 3 in eqn. (I), we get

3 – q = – 2

q = 3+2

q = 5

So, p = 3 and q = 5.

Hence, the fraction p/q is 3/5.

(ii)五年前，努里(Nuri)的年龄是索努(Sonu)的三倍。十年后，努里(Nuri)的年龄将是索努(Sonu)的两倍。努里(Nuri)和索努(Sonu)几岁?

解决方案：

Let us assume, present age of Nuri is x

And present age of Sonu is y.

Here, According to the given condition, the equation formed will be as follows :

x – 5 = 3(y – 5)

x – 3y = – 10 …………………………………..(I)

Now,

x + 10 = 2(y +10)

x – 2y = 10 …………………………………….(II)

Subtract eqn. (I) from (II), we get

y = 20

Now putting y = 20 in eqn. (II), we get

x – 2(20) = 10

x = 10+40

x = 50

Hence, 

Age of Nuri is 50 years

Age of Sonu is 20 years.

(iii)两位数字的数字总和为9。此外，此数字的9倍是通过反转数字的顺序获得的数字的两倍。查找号码。

解决方案：

Let the unit digit and tens digit of a number be x and y respectively.

Then, Number = 10y + x

And, reverse number = 10x + y

eg: 23 

x = 3 and y = 2

So, 23 can be represented as = 10(2) + 3 = 23

Here, According to the given condition

x + y = 9 …………………….(I)

and,

9(10y + x) = 2(10x + y)

90y + 9x = 20x + 2y

88y = 11x

x = 8y 

x – 8y = 0 ………………………………………………………….. (II)

Subtract eqn. (II) from (I) we get,

9y = 9

y = 1

Now putting y = 1 in eqn. (II), we get

x – 8(1) = 0

x = 8

Hence, the number is 10y + x 

=10 × 1 + 8 

Number = 18

(iv)米娜去银行提取2000卢比。她要求收银员只给她50卢比和100卢比的钞票。 Meena总共收到25张音符。找出她收到了₹50和₹100的多少张钞票。

解决方案：

Let the number of ₹ 50 notes be x and the number of ₹100 notes be y

Here, According to the given condition

x + y = 25 ……………………………….. (I)

50x + 100y = 2000 ………………………………(II)

Divide (II) by 50 and then subtract (I) from it.

y = 15

Now putting y = 15 in eqn. (I), we get

x + 15 = 25

x = 10

Hence, Manna has 10 notes of ₹ 50 and 15 notes of ₹ 100.

(v)借书图书馆前三天收取固定费用，其后每天收取一笔额外费用。莎莉莎为一本保存了七天的书支付了27卢比，而苏西为她一本保存了五天的书支付了21卢比。查找固定费用和每一天的费用。

解决方案：

Let the fixed charge for the first three days be ₹ x and,

The charge for each day extra be ₹ y.

Here, According to the given condition,

x + 4y = 27 …….…………………………. (I)

x + 2y = 21 ………………………………………….. (II)

Subtract (II) from (I), we get

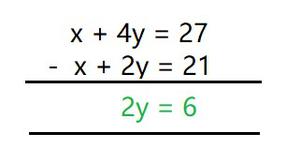
2y = 6

y = 3

Now putting y = 3 in eqn. (II), we get

x + 4(3) = 27

x = 27 – 12

x = 15

Hence, the fixed charge is ₹15

And the Charge per day is ₹ 3