Class 11 RD Sharma解决方案–第20章几何级数-练习20.3 |套装2

问题12：求和： $\sum_{n=1}^{10}(\frac{1}{2})^{n-1}+(\frac{1}{5})^{n+1}$

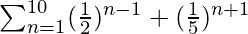
解决方案：

Given summation can be written as,

S = $\sum_{n=1}^{10}(\frac{1}{2})^{n-1}+\sum_{n=1}^{10}(\frac{1}{5})^{n+1}$ 

= (1 + 1/2 + 1/2² + . . . . 10 terms) + (1/5² + 1/5³ + 1/5⁴ + . . . . 10 terms)

= $\left[\frac{1-\frac{1}{2^{10}}}{1-\frac{1}{2}}\right]+\left[\frac{1-\frac{1}{5^{10}}}{1-\frac{1}{5}}\right]$

= $\frac{2^{10}-1}{2^9}+\frac{5^{10}-1}{4(5^{11})}$

Therefore, sum of the series is $\frac{2^{10}-1}{2^9}+\frac{5^{10}-1}{4(5^{11})}$.

问题13. GP的第五项为81，而第二项为24。找到其前八个项的序列和总和。

解决方案：

We know nth term of G.P. is given by, a_n = ar^n-1.

According to the question, we have,

=> ar⁴ = 81 . . . . (1)

=> ar = 24 . . . . (2)

Dividing (2) by (1),

=> r³ = 81/24

=> r³ = 27/8

=> r = 3/2

Putting r = 3/2 in (2), we get,

=> a = (24)(2)/3

=> a = 16

We know sum of n terms of G.P. is given by, S_n = a(rⁿ−1)/(r−1).

So, S₈ = 16[(3/2)⁸−1]/[(3/2)−1]

= 16[3⁸ − 2⁸]/2⁷

= 6305/8

As a = 16 and r = 3/2, series would be 16, 24, 36, 54, . . . . 

Also, the sum of first 8 terms of G.P. is 6305/8.

问题14.如果S ₁ ，S ₂ ，S ₃分别是GP的n，2n，3n项之和，则证明S ² ₁ + S ² ₂ = S ₁ (S ₂ + S ₃ )。

解决方案：

We are given,

S₁ = Sum of n terms = a[1−rⁿ]/(1−r)

S₂ = Sum of 2n terms = a[1−r²ⁿ]/(1−r)

S₃ = Sum of 3n terms = a[1−r³ⁿ]/(1−r)

We have, 

L.H.S. = S²₁+S²₂

= $\left[\frac{a(1-r^n)}{1-r}\right]^2+\left[\frac{a(1-r^{2n})}{1-r}\right]^2$

= $\frac{a^2}{(1-r)^2}[(1-r^n)^2+(1-r^{2n})^2]$

= $\frac{a^2}{(1-r)^2}[1+r^{2n}-2r^n+1+r^{4n}-2r^{2n}]$

= $\frac{a^2}{(1-r)^2}[2-r^{2n}-2r^n+r^{4n}]$

And R.H.S. = S₁(S₂+S₃)

= $\frac{a(1-r^n)}{1-r}\left[\frac{a(1-r^{2n})}{1-r}+\frac{a(1-r^{3n})}{1-r}\right]$

= $\frac{a^2}{(1-r)^2}[(1-r^n)(1-r^{2n})+(1-r^n)(1-r^{3n})]$

= $\frac{a^2}{(1-r)^2}[1-r^{2n}-r^n+r^{3n}+1-r^{3n}-r^n+r^{4n}]$

= $\frac{a^2}{(1-r)^2}[2-r^{2n}-2r^n+r^{4n}]$

= L.H.S.

Hence, proved.

问题15显示，一个GP的n项的总和与项的和从第(n + 1)到^第(2N)^个术语的比率为1 / R ^N。

解决方案：

We know sum of n terms of a G.P. is given by, S₁ = a[1−rⁿ]/(1−r).

And sum of terms from (n+1)^th to (2n)^th term will be,

S₂ = arⁿ + arⁿ⁺¹ + arⁿ⁺² + . . . . ar^2n-1

= arⁿ[1−rⁿ]/(1−r)

L.H.S. = 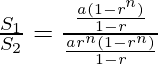$\frac{S_1}{S_2} = \frac{\frac{a(1-r^n)}{1-r}}{\frac{ar^n(1-r^n)}{1-r}}$

= 1/rⁿ

= R.H.S.

Hence, proved.

问题16。如果a和b是x ² – 3x + p = 0的根，而c，d是x ² – 12x + q = 0的根，其中a，b，c，d构成一个GP证明( q + p)：( q – p)= 17:15。

解决方案：

We are given that a, b, c, d are in G.P. Let’s suppose the common ratio is r.

So, b=ar, c=ar² and d=ar³

Now a and b are the roots of x² – 3x + p = 0.

Sum of roots = a + b = 3  

=> a + ar = 3  

=> a(1+r) = 3 ….. (1)

Product of roots = ab = p

=> a(ar) = p

=> a²r = p  ….. (2)

And c, d are the roots of x² − 12x + q = 0

Sum of roots = c + d = 12

=> ar² + ar³ = 12

=> ar²(1+r) = 12  ….. (3)

Product of roots = cd = q

=> ar²(ar³) = q

=> a²r⁵ = q  ….. (4)

Dividing equation (3) by (1), we get,

=> $\frac{ar^2(1+r)}{a(1+r)}$ = $\frac{12}{3}$

=> r² = 4

=> r = ±2

When r=2, from (1), we get,

=> a(1+2) = 3

=> a = 1

Putting a=1 and r=2 in (2),

=> p = (1)²(2) = 2

From (4) we get,

q = (1)²(2)⁵ = 32

Now L.H.S. = $\frac{q+p}{q−p}$ = $\frac{32+2}{32−2}$ = $\frac{34}{30}$ = $\frac{17}{15}$

= R.H.S.  

When r=−2, from (1), we get,

=> a(1−2) = 3

=> a = −3

Putting a=−3 and r=−2 in (2),

p = (−3)²(−2) = −18

From (4) we get,

q = (−3)²(−2)⁵ = −288

Now L.H.S. = $\frac{q+p}{q−p}$ = $\frac{−288+(−18)}{−288−(−18)}$ = $\frac{−306}{−270}$ = $\frac{17}{15}$

= R.H.S.

Hence, proved.

问题17.总和3069/512需要多少个GP 3、3 / 2、3 / 4，…?

解决方案：

Given G.P. has first term(a) = 3, common ratio(r) = (3/2)/3 = 1/2 and sum of terms(S_n) = 3069/512.

We know sum of n terms of a G.P. is given by S_n = a(rⁿ–1)/(r–1).

=> 3069/512 = 3[1–(1/2)ⁿ] / [1–(1/2)]

=> 2(2ⁿ–1)/(2ⁿ) = 1023/512

=> 1023(2)ⁿ = 1024(2)ⁿ – 1024

=> 2ⁿ = 1024

=> n = 10

Therefore, 10 terms of the G.P. should be taken together to make 3069/512.

问题18.一个人有2个父母，4个祖父母，8个曾祖父母，依此类推。找出他祖先十代中祖先的数量。

解决方案：

We have the sequence, 2,4,8, . . . . which forms a G.P. with first term(a) = 2 and common ratio(r) = 4/2 = 2.

 We know sum of n terms of a G.P. is given by S_n = a(rⁿ–1)/(r–1).

Number of ancestors during the ten generations = Sum of first 10 terms of the G.P. 

S₁₀ = 2(2¹⁰–1)/(2–1)

= 2(1023)

= 2046

Therefore, the number his ancestors during the ten generations preceding his own is 2046.

问题19，S ₁ ，S ₂ ，S ₃ ，…。 。 。 …，S _n是总和n个方面GP的，其第一项是1中的每个和公共比例1,2,3，。 。 。 ，分别证明S ₁ + S ₂ + 2S ₃ + 3S ₄ +。 。 。 。 +(n–1)S _n = 1 ⁿ + 2 ⁿ + 3 ⁿ +。 。 。 。 + n ⁿ 。

解决方案：

S₁, S₂, S₃, . . . ., S_n are the sums of n terms of G.P.’s whose first term is 1 in each and common ratios are 1,2,3, . . . ., n respectively. 

Here for S₁, series will be 1,1,1,1, . . . up to n terms as first term(a) and common ratio(r) both are equal to 1.

So, S₁ = 1+1+1+1+ . . . . up to n terms = n

So, L.H.S. = S₁ + S₂ + 2S₃ + 3S₄ + . . . . + (n–1)S_n

= $n+\frac{2^n-1}{2-1}+2(\frac{3^n-1}{3-1})+3(\frac{4^n-1}{4-1})+....+(n-1)(\frac{n^n-1}{n-1})$

= n + (2ⁿ – 1) + (3ⁿ – 1) + (4ⁿ – 1) + . . . . (nⁿ – 1)

= n + (2ⁿ + 3ⁿ + 4ⁿ +. . . . + nⁿ) – (1 + 1 +1 + 1 + . . . . (n–1) terms)

= n + (2ⁿ + 3ⁿ + 4ⁿ +. . . . + nⁿ) – n + 1

= 1 + 2ⁿ + 3ⁿ + 4ⁿ +. . . . + nⁿ

= 1ⁿ + 2ⁿ + 3ⁿ + 4ⁿ +. . . . + nⁿ

= R.H.S.

Hence, proved.

问题20. GP由偶数个词组成。如果所有项的总和是占据奇数位的项的总和的5倍。找出GP的共同比例

解决方案：

As number of terms is even, let the number of terms of the G.P. be 2n.

According to the question,

Sum of all terms = 5 (Sum of the terms occupying the odd places)

=> a₁ + a₂ + a₃ + . . . . + a_n = 5 (a₁ + a₃ + a₅ + . . . . a_2n–1)

=> a + ar + ar² + . . . . + ar^n–1 = 5 (a + ar² + ar⁴ + . . . . + ar^2n–2)

=> a(1–r²ⁿ)/(1–r) = 5a(1–r²ⁿ)/(1–r²)

=> a/(1–r) = 5a/(1–r²)

=> a/(1–r) = 5a/[(1–r)(1+r)]

=> 5/(1+r) = 1

=> 1+r = 5

=> r = 4

Therefore, the common ratio of the G.P. is 4.

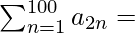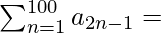问题21.设_n为正数GP的第n个项。让$\sum_{n=1}^{100} a_{2n} = α$和$\sum_{n=1}^{100} a_{2n-1} = β$ ，使得α≠β 。证明GP的公共比率为α/β。

解决方案：

We have, $\sum_{n=1}^{100} a_{2n} = α$

=> a₂ + a₄ + a₆ + . . . . + a₂₀₀ = α 

=> ar + ar³ + ar⁵ + . . . . + ar¹⁹⁹ = α

=> ar(r²⁽¹⁰⁰⁾–1)/(r–1) = α

=> ar(r²⁰⁰–1)/(r–1) = α . . . . (1)

Also we have, $\sum_{n=1}^{100} a_{2n-1} = β$

=> a₁ + a₃ + a₅ + . . . . + a₁₉₉ = β

=> a + ar² + ar⁴ + . . . . + ar¹⁹⁸ = β

=> a(r²⁽¹⁰⁰⁾–1)/(r–1) = β

=> a(r²⁰⁰–1)/(r–1) = β . . . . (2)

Dividing (2) by (1), we get,

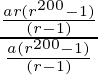=> $\frac{\frac{ar(r^{200}-1)}{(r-1)}}{\frac{a(r^{200}-1)}{(r-1)}}$ = $\frac{α}{β}$

=> r = $\frac{α}{β}$

Hence, proved.

问题22。找到该系列的2n个项的总和，其每个偶数项是“ a”乘以其前一个项，而每个奇数项是“ c”乘以其前一项，第一个项是1。

解决方案：

Suppose we have the series, a₁,a₂,a₃, . . . . a_n.

According to the question, we have, a₁ = 1, a₂ = a, a₃ = ca, a₄ = a²c, a₅ = a²c² and so on.

Now, sum of 2n terms of the series = a₁ + a₂ + a₃ + . . . . + a_2n

S_2n = 1 + a + ca + a²c + a²c² + . . . . 2n terms

= (1+a) + ca(1+a) + a²c²(1+a) + . . . . n terms

Now this is a G.P. with first term(a) = (1+a) and common ratio(r) = ca. So, we get

S_2n = $\frac{(1+a)[(ac)^n-1]}{ac-1}$

Therefore, sum of 2n terms of the series is $\frac{(1+a)[(ac)^n-1]}{ac-1}$.