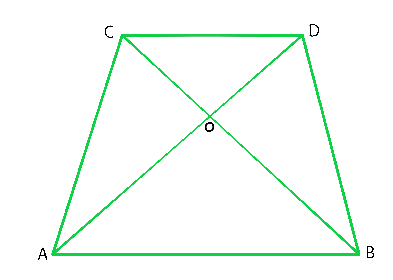
问题1.下面给出的是平行四边形ABCD。完成每个语句以及所使用的定义或属性。
(i)广告=
(ii)∠DCB=
(iii)OC =
(iv)DAB + CDA =
解决方案:
(i) AD = BC. Because, diagonals bisect each other in a parallelogram.
(ii) ∠DCB = ∠BAD. Because, alternate interior angles are equal.
(iii) OC = OA. Because, diagonals bisect each other in a parallelogram.
(iv) ∠DAB+ ∠CDA = 180°. Because sum of adjacent angles in a parallelogram is 180°.
问题2.下图是平行四边形。求出未知数x,y,z的度值。

解决方案:
(i) From figure we conclude that,
∠ABC = ∠y = 100o (Opposite angles are equal in a parallelogram)
∠x + ∠y = 180o (sum of adjacent angles is = 180° in a parallelogram)
∠x + 100° = 180°
∠x = 180° – 100° = 80°
Hence, ∠x = 80° ∠y = 100° ∠z = 80° (opposite angles are equal in a parallelogram)
(ii) From figure we conclude that,
∠RSP + ∠y = 180° (sum of adjacent angles is = 180° in a parallelogram)
∠y + 50° = 180°
∠y = 180° – 50° = 130°
Hence, ∠x = ∠y = 130° (opposite angles are equal in a parallelogram)
From figure, we conclude that,
∠RSP = ∠RQP = 50° (opposite angles are equal in a parallelogram)
∠RQP + ∠z = 180° (linear pair)
50° + ∠z = 180°
∠z = 180° – 50° = 130°
Hence, ∠x = 130°, ∠y = 130° and ∠z = 130°.
(iii) As we know that,
In ΔPMN ∠NPM + ∠NMP + ∠MNP = 180° (Sum of all the angles of a triangle is 180°)
30° + 90° + ∠z = 180°
∠z = 180°-120° = 60°
From figure, we conclude that,
∠y = ∠z = 60° (opposite angles are equal in a parallelogram)
∠z = 180°-120° (sum of the adjacent angles is equal to 180° in a parallelogram)
∠z = 60°
∠z + ∠LMN = 180° (sum of the adjacent angles is equal to 180° in a parallelogram)
60° + 90°+ ∠x = 180°
∠x = 180°-150° = 30°
Hence, ∠x = 30° ∠y = 60° ∠z = 60°
(iv) From figure we conclude that,
∠x = 90° [vertically opposite angles are equal]
In ΔDOC, ∠x + ∠y + 30° = 180° (Sum of all the angles of a triangle is 180°)
90° + 30° + ∠y = 180°
∠y = 180°-120°
∠y = 60°
∠y = ∠z = 60° (alternate interior angles are equal)
Hence, ∠x = 90° ∠y = 60° ∠z = 60°
(v) From figure we conclude that,
∠x + ∠POR = 180° (sum of the adjacent angles is equal to 180° in a parallelogram)
∠x + 80° = 180°
∠x = 180°-80° = 100°
∠y = 80° (opposite angles are equal in a parallelogram)
∠SRQ =∠x = 100°
∠SRQ + ∠z = 180° (Linear pair)
100° + ∠z = 180°
∠z = 180°-100° = 80°
Hence, ∠x = 100°, ∠y = 80° and ∠z = 80°.
(vi) From figure we conclude that,
∠y = 112° (In a parallelogram opposite angles are equal)
∠y + ∠VUT = 180° (In a parallelogram sum of the adjacent angles is equal to 180°)
∠z + 40° + 112° = 180°
∠z = 180°-152° = 28°
∠z =∠x = 28° (alternate interior angles are equal)
Hence, ∠x = 28°, ∠y = 112°, ∠z = 28°.
问题3.下图可以是平行四边形吗?证明你的答案。

解决方案:
(i) No, as we know that opposite angles are equal in a parallelogram.
(ii) Yes, as we know that opposite sides are equal and parallel in a parallelogram.
(iii) No, as we know that the diagonals bisect each other in a parallelogram.
问题4.在下图中,HOPE是平行四边形。找到角度量度x,y和z。陈述您用来找到它们的几何真相。

解决方案:
As we know that,
∠POH + 70° = 180° (Linear pair)
∠POH = 180°-70° = 110°
∠POH = ∠x = 110° (opposite angles are equal in a parallelogram)
∠x + ∠z + 40° = 180° (sum of the adjacent angles is equal to 180° in a parallelogram)
110° + ∠z + 40° = 180°
∠z = 180° – 150° = 30°
∠z +∠y = 70°
∠y + 30° = 70°
∠y = 70°- 30° = 40°
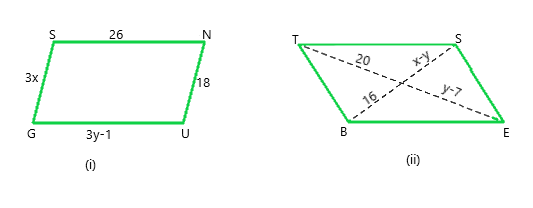
问题5.在下图中, GUNS和RUNS是平行四边形。找出x和y。
解决方案:
From figure, we conclude that,
(i) 3y – 1 = 26 (opposite sides are of equal length in a parallelogram)
3y = 26 + 1
y = 27/3 = 9
3x = 18 (opposite sides are of equal length in a parallelogram)
x = 18/3= 6
Hence, x = 6 and y = 9
(ii) y – 7 = 20 (diagonals bisect each other in a parallelogram)
y = 20 + 7 = 27
x – y = 16 (diagonals bisect each other in a parallelogram)
x -27 = 16
x = 16 + 27 = 43
Hence, x = 43 and y = 27
问题6.在下图中,“风险”和“线索”是平行四边形。求x的度量。

解决方案:
From figure, we conclude that,
In parallelogram RISK
∠RKS + ∠KSI = 180° (sum of the adjacent angles is equal to 180° in a parallelogram)
120° + ∠KSI = 180°
∠KSI = 180° – 120° = 60°
In parallelogram CLUE,
∠CEU = ∠CLU = 70° (opposite angles are equal in a parallelogram)
In ΔEOS,
70° + ∠x + 60° = 180° (Sum of angles of a triangles is 180°)
∠x = 180° – 130° = 50°
Hence, x = 50°
问题7.平行四边形的两个相反角度是(3x – 2)°和(50 – x)°。找到平行四边形的每个角度的度量。
解决方案:
As we know that the opposite angles of a parallelogram are equal.
So, (3x – 2)° = (50 – x)°
3xo – 2° = 50° – x°
3x° + xo = 50° + 2°
4x° = 52°
xo = 52°/4 = 13°
The opposite angles are,
(3x – 2)° = 3×13 – 2 = 37°
(50 – x)° = 50 – 13 = 37°
As we know that Sum of adjacent angles = 180°
Other two angles are 180° – 37° = 143°
Hence, Measure of each angle is 37°, 143°, 37°, 143°.
问题8.如果平行四边形的角度是其相邻角度的三分之二,请找出平行四边形的角度。
解决方案:
Let us assume that one of the adjacent angle as x°,
then other adjacent angle is = 2x°/3
As we know that sum of adjacent angles = 180°
Therefore,
x° + 2x°/3 = 180°
(3x° + 2x°)/3 = 180°
5x°/3 = 180°
x° = 180°×3/5 = 108°
Other angle is = 180° – 108° = 72°
Hence, Angles of a parallelogram are 72°, 72°, 108°, 108°.
问题9.平行四边形的一个角度的大小为70°。其余角度的尺寸是多少?
解决方案:
Let us assume that the one of the adjacent angle as x°
Other adjacent angle = 70°
As we know that sum of adjacent angles = 180°
Therefore,
x° + 70° = 180°
x° = 180° – 70° = 110°
Hence, Measures of the remaining angles are 70°, 70°, 110° and 110°
问题10:平行四边形的两个相邻角度为1:2。找到平行四边形的所有角度的度量。
解决方案:
Let us assume that one of the adjacent angle as x°,
then other adjacent angle = 2x°
As we know that sum of adjacent angles = 180°
Therefore,
x° + 2x° = 180°
3x° = 180°
x° = 180°/3 = 60°
So other angle is 2x = 2×60 = 120°
Hence, Measures of the remaining angles are 60°, 60°, 120° and 120°
问题11:在平行四边形ABCD中,∠D= 135°,确定∠A和∠B的量度。
解决方案:
Given that,
one of the adjacent angle ∠D = 135°
Let us assume that other adjacent angle ∠A be = x°
As we know that sum of adjacent angles = 180°
x° + 135° = 180°
x° = 180° – 135° = 45°
∠A = x° = 45°
As we know that the opposite angles are equal in a parallelogram.
Therefore, ∠A = ∠C = 45°
and ∠D = ∠B = 135°.
问题12. ABCD是一个平行四边形,其中∠A= 70°。计算∠B,∠C和∠D。
解决方案:
Given that,
one of the adjacent angle ∠A = 70°
and other adjacent angle ∠B is = x°
As we know that sum of adjacent angles = 180°
x° + 70° = 180°
x° = 180° – 70° = 110°
∠B = x° = 110°
As we know that the opposite angles are equal in a parallelogram.
Therefore, ∠A = ∠C = 70°
and ∠D = ∠B = 110°
问题13:平行四边形的两个相反角度的和为130°。找到平行四边形的所有角度。
解决方案:
From figure, we conclude that, ABCD is a parallelogram
∠A + ∠C = 130°
Here ∠A and ∠C are opposite angles
Therefore ∠C = 130/2 = 65°
As we know that sum of adjacent angles is 180
∠B + ∠D = 180
65 + ∠D = 180
∠D = 180 – 65 = 115
∠D = ∠B = 115 (Opposite angles)
Hence, ∠A = 65°, ∠B = 115°, ∠C = 65° and ∠D = 115°.
问题14.四边形的所有角度都相等。找到每个的度量。四边形是平行四边形吗?什么是平行四边形的特殊类型?
解决方案:
Let us assume that each angle of a parallelogram as xo
As we know that sum of angles = 360°
x° + x° + x° + x° = 360°
4 x° = 360°
x° = 360°/4 = 90°
Hence, each angle is 90°
Yes, this quadrilateral is a parallelogram.
Since each angle of a parallelogram is equal to 90°, so it is a rectangle.
问题15:平行四边形的两个相邻边分别为4 cm和3 cm。找到它的周长。
解决方案:
As we know that opposite sides of a parallelogram are parallel and equal.
therefore, Perimeter = Sum of all sides (there are 4 sides)
Perimeter = 4 + 3 + 4 + 3 = 14 cm
Hence, Perimeter is 14 cm.