问题1:以下哪些陈述是正确的,哪些是错误的?给出答案的理由。
(i)一条线只能穿过一个点。
(ii)有无限多的线穿过两个不同的点。
(iii)可以在两侧无限期地产生终止线。
(iv)如果两个圆相等,则它们的半径相等。
(v)在给定的图中,如果AB = PQ并且PQ = XY,则AB = XY。
解决方案:
(i) False
Reason: If we mark a point O on the surface of a paper. Using pencil and scale, we can draw infinite number of straight lines passing through O.
(ii) False
Reason: Through two distinct points there can be only one line that can be drawn. Hence, the statement mentioned above is False.
(iii) True
Reason: A line that is terminated can be indefinitely produced on both sides as a line can be extended on both its sides infinitely. Hence, the statement mentioned above is True.
(iv) True
Reason: The radii of two circles are equal when the two circles are equal. The circumference and the centre of both the circles coincide; and thus, the radius of the two circles should be equal. Hence, the statement mentioned above is True.
(v) True
Reason: According to Euclid’s 1st axiom- “Things which are equal to the same thing are also equal to one another”. Hence, the statement mentioned above is True.
问题2:为以下每个术语给出定义。是否需要首先定义其他术语?它们是什么,您将如何定义它们?
(i)平行线
(ii)垂直线
(iii)线段
(iv)圆的半径
(v)广场
解决方案:
Yes, there are other terms which need to be defined first, so that we understand better:
- Plane: Flat surfaces in which geometric figures can be drawn are known are plane. A plane surface is a surface which lies evenly with the straight lines on itself.
- Point: A dimensionless dot which is drawn on a plane surface is known as point. A point is that which has no part.
- Line: A collection of points that has only length and no breadth is known as a line. And it can be extended on both directions. A line is breadth-less length.
(i) Parallel lines: Two lines l and m in a plan are said to be parallel if they have a no common point and we can write them as l || m.

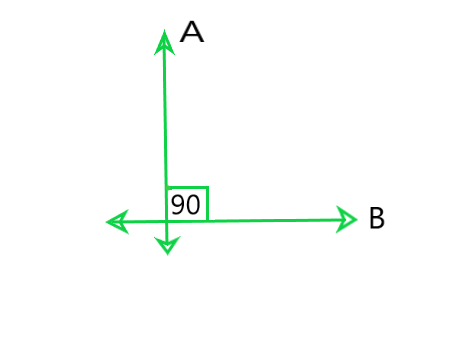
(ii) Perpendicular lines: Two lines A and B are said to be perpendicular if the form a right angle and we can write them as A ⊥ B.
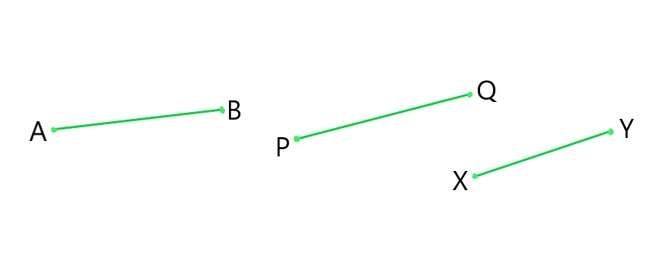
(iii) Line Segment: A line segment is a part of line and having a definite length. It has two end-points. In the figure, a line segment is shown having end points P and Q. Write it as arrow over PQ.

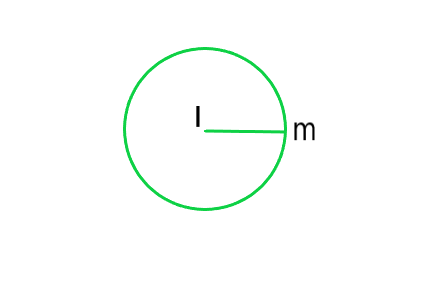
(iv) Radius of Circle: The distance from the centre to a point on the circle is called the radius of the circle. In the figure, l is centre and m is a point on the circle, then lm is the radius of the circle.
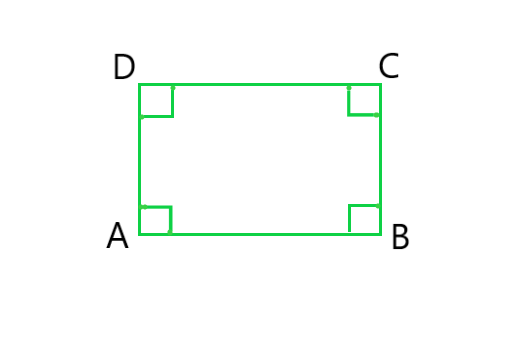
(v) Square: A quadrilateral in which all the four angles are right angles and all the four sides are equal is called a Square
In the given figure ABCD is a Square.
问题3:考虑下面给出的两个“假设”:
(i)给定两个不同的点A和B,在A和B之间存在第三个点C。
(ii)至少存在三个不在同一直线上的点。
这些假设是否包含任何未定义的术语?这些假设是否一致?
他们遵循欧几里得的假设吗?解释。
解决方案:
Yes, these postulates contain undefined terms such as ‘Point and Line’. Undefined terms in the postulates are:
- There are many points that lie in a plane. But, in the postulates as given here, the position of the point C is not given, as of whether it lies on the line segment joining AB or it is not joining line segment.
- On top of that, there is no information about whether the points are in same plane or not.
And
Yes, these postulates are consistent when we deal with these two situations:
- Point C is lying on the line segment AB in between A and B.
- Point C does not lie on the line segment AB.
No, they don’t follow from Euclid’s postulates. They follow the axioms i.e “Given two distinct points, there is a unique line that passes through them.”
问题4:如果点C位于两个点A和B之间,使得AC = BC,则证明AC = 12 AB,并通过绘制图进行说明。
解决方案:
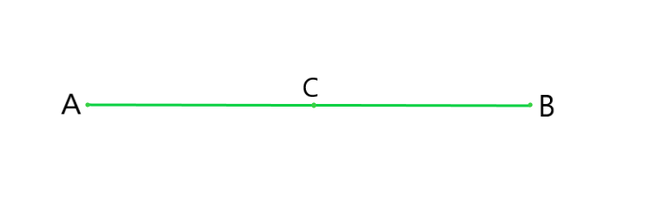
AC = BC (Given)
As we have studied in this chapter “If equals are added to equals then there wholes are also equal”.
Therefore, AC + BC = BC + AC
⇒ 2AC = BC+AC
As we have studied in this chapter, we know that,
BC+AC = AB (as it coincides with line segment AB)
∴ 2 AC = AB (If equals are added to equals, the wholes are equal).
⇒ AC = (½)AB.
问题5:在问题4中,点C称为线段AB的中点。证明每个线段只有一个中点。
解决方案:
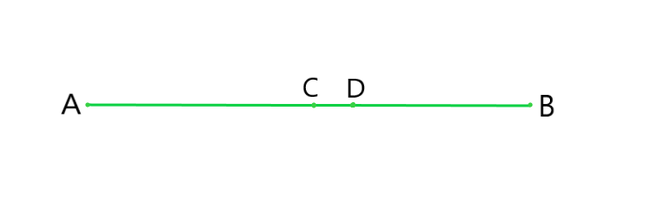
Let, AB be the line segment as given in the Question.
Assume that points C and D are the two different mid points of line segment AB.
Therefore, C and D are the midpoints of AB.
Now, as C and D are mid points of Ab we have,
AC = CB and AD = DB
CB+AC = AB (as it coincides with line segment AB)
Similarly, DB+AD = AB.
Now,
Adding AC to the L.H.S and R.H.S of the equation AC = CB
We get, AC+AC = CB+AC (If equals are added to equals, the wholes are equal.)
⇒ 2AC = AB — (i)
Similarly,
2 AD = AB — (ii)
From equation (i) and (ii), Since R.H.S are same, we equate the L.H.S we get,
2 AC = 2 AD (Things which are equal to the same thing are equal to one another.)
⇒ AC = AD (Things which are double of the same things are equal to one another.)
Thus, we conclude that C and D are the same points.
This contradicts our assumption that C and D are two different mid points of AB.
Thus, it is proved that every line segment has one and only one mid-point.
Hence, Proved.
问题6:在图中,如果AC = BD,则证明AB = CD。
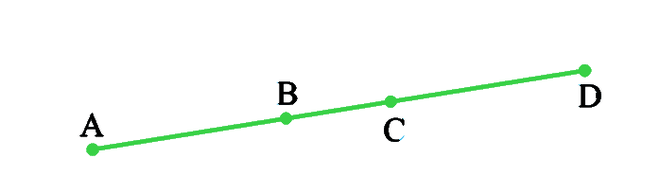
解决方案:
According to the question, AC = BD
From the given figure we can conclude that,,
AC = AB+BC
BD = BC+CD
⇒ AB+BC = BC+CD (AC = BD, given)
As we have studied, according to Euclid’s axiom, when equals are subtracted from equals, remainders are also equal.
Subtracting BC from the L.H.S and R.H.S of the equation AB+BC = BC+CD, we get,
AB+BC-BC = BC+CD-BC
AB = CD
Hence Proved.
问题7:为什么在欧几里得公理列表中的公理5被认为是“普遍真理”? (请注意,问题与第五种假设无关)。
解决方案:
Euclid’s fifth axiom states that “the whole is greater than the part.”
For Example: A cake. When it is whole or complete, assume that it measures 2 pounds but when a part from it is taken out and measured, its weight will be smaller than the previous measurement. So, the fifth axiom of Euclid is true for all the materials in the universe. Hence, Axiom 5, in the list of Euclid’s axioms, is considered a ‘universal truth’.