第 12 类 RD Sharma 解——第 19 章不定积分——练习 19.4

问题 1. 整合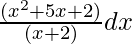$∫ \frac{(x^2 + 5x +2)}{(x + 2)} dx$

解决方案：

 Let, I = $∫ \frac{(x^2 + 5x +2)}{(x + 2)} dx$

Use division method, then we get,

$\frac{(x2 + 5x +2)}{(x+2)} = x + 3 - \frac{4}{(x+2)}$

$∫ \frac{(x^2 + 5x +2)}{(x + 2)} =∫ x + 3 - \frac{4}{(x+2)} dx$

= ∫ (x + 3)dx – 4∫1/(x + 2) dx

Integrate the above equation, then we get

= x²/2 + 3x – 4 log |x + 2| + c

Hence, I = x²/2 + 3x – 4 log |x + 2| + c 

问题 2. 整合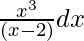$∫ \frac{x^3}{(x-2)} dx$

解决方案：

Let I = $∫ \frac{x^3}{(x-2)} dx$

Use division method, then we get,

$\frac{x^3}{(x+2)} =x^2 + 2x + 4 + \frac{8}{(x-2)}$

= ∫ x² dx + 2∫x dx + 4∫ dx + 8 ∫1/(x – 2) dx

Integrate the above equation, then we get

= x³/3 + 2x²/2 + 4x + 8 log|x – 2| + c

= x³/3 + x² + 4x + 8 log|x – 2| + c      

Hence, I = x³/3 + x² + 4x + 8 log|x – 2| + c  

问题 3. 整合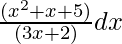$∫ \frac{(x^2 + x + 5)}{(3x +2)} dx$

解决方案：

Let, I = $∫ \frac{(x^2 + x + 5)}{(3x +2)} dx$

Use division method, then we get,

$\frac{(x^2 + x + 5)}{(3x +2)} = \frac{x}{3} + \frac{1}{9} + \frac{43}{9}\times \frac{1}{3x+2} dx$

= $∫\frac{x}{3}dx + \frac{1}{9}∫1dx + \frac{43}{9} ∫\frac{1}{(3x+2)} dx$

Integrate the above equation, then we get

= $\frac{x^2}{6} + \frac{x}{9} + \frac{43}{9} \frac{1}{3} log|3x+2| + c$

= x² /6 + x/9 + (43/27) log|3x + 2| + c

Hence, I = = x² /6 + x/9 + (43/27) log|3x + 2| + c

问题 4. 整合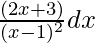$∫ \frac{(2x+3)}{(x-1)^2} dx$

解决方案：

Let, I = $∫ \frac{(2x+3)}{(x-1)^2} dx$

We can write the above equation as below,

= $∫ \frac{(2x + 2 - 2 + 3)}{(x-1)^2} dx$

On solving the above equation,

= $∫ \frac{(2x - 2 + 5)}{(x-1)^2} dx$

= $∫ \frac{2(x - 1)}{(x-1)^2} dx + 5 ∫\frac{1}{(x-1)^2} dx$

= 2∫ (1/(x – 1) dx + 5 ∫(x – 1)^-2 dx

Integrate the above equation, then we get

= 2 log|x – 1| + 5 (x – 1)^-1/(-1) + c

= 2 log|x – 1| – 5 / (x – 1) + c

Hence, I = 2 log|x – 1| – 5 / (x – 1) + c

问题 5. 整合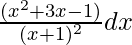$∫ \frac{(x^2 + 3x - 1)}{(x+1)^2} dx$

解决方案：

Let, I = $∫ \frac{(x^2 + 3x - 1)}{(x+1)^2} dx$

We can write the above equation as below,

= $∫\frac{(x^2 + x + 2x - 1)}{(x+1)^2} dx$

=$∫\frac{x(x+1)}{(x+1)^2} dx + ∫\frac{(2x - 1)}{(x+1)^2} dx$

= $∫\frac{x}{(x+1)} dx + ∫\frac{\sqrt{2x + 2 - 2 + 1}}{(x+1)^2} dx$

= $∫\frac{(x+1)}{(x+1)} dx - ∫\frac{1}{(x+1)} dx + 2∫\frac{(x + 1)}{(x+1)^2} dx - 3∫\frac{1}{(x+1)^2} dx$

= ∫ dx – ∫ 1/ (x + 1) dx + 2∫1/(x + 1) dx -3 ∫(x + 1)^-2 dx

Integrate the above equation, then we get

= x – log|x + 1| + 2 log|x + 1| – 3(x + 1)^-1/(-1) + c  

= x – log|x + 1| + 2 log|x + 1| + 3/(x + 1) + c

= x + log|x + 1| + 3/(x + 1) + c

Hence, I = x + log|x + 1| + 3/(x + 1) + c

问题 6. 整合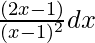$∫ \frac{(2x - 1)}{(x - 1)^2} dx$

解决方案：

Let, I =$∫ \frac{(2x - 1)}{(x - 1)^2} dx$

= $∫ \frac{(2x - 1 + 2 - 2)}{(x - 1)^2} dx$

= $∫ \frac{(2x - 2 + 1)}{(x - 1)^2} dx$

= $∫ \frac{(2x - 2)}{(x - 1)^2} dx+ ∫\frac{1}{(x - 1)^2} dx$

= $2∫ \frac{(x - 1)}{(x - 1)^2} dx+ ∫\frac{1}{(x - 1)^2} dx$

= 2∫ 1/(x – 1) dx + ∫(x – 1)^-2 dx

Integrate the above equation, then we get

= 2 log|x – 1| + (x – 1)^-1/(-1) + c

= 2 log|x – 1| – 1/(x – 1) + c

Hence, I = 2 log|x – 1| – 1/(x – 1) + c