第 12 类 RD Sharma 解决方案 - 第 5 章矩阵代数 - 练习 5.3 |设置 3
问题 52. 如果 A = 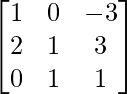 ,然后验证 A 2 + A = A (A + I),其中 I 是单位矩阵。
,然后验证 A 2 + A = A (A + I),其中 I 是单位矩阵。
解决方案:
We have,
A =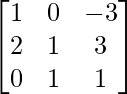
A2 =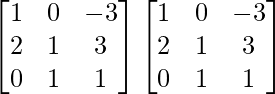
=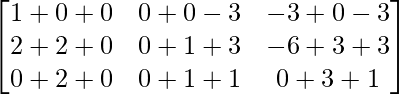
=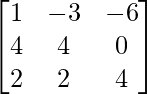
L.H.S. = A2 + A
=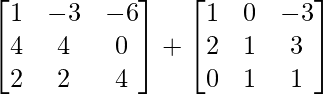
=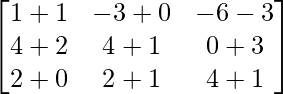
=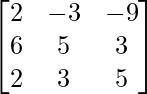
R.H.S. = A (A + I)
=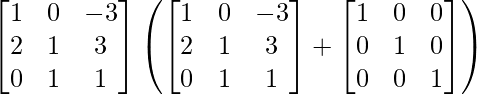
=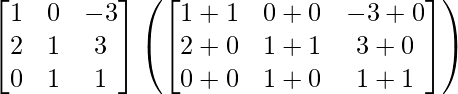
=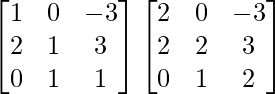
=
=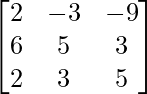
= L.H.S.
Hence proved.
问题 53. 如果 A = 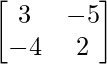 ,然后找到 A 2 – 5A – 14I。因此获得 A 3 。
,然后找到 A 2 – 5A – 14I。因此获得 A 3 。
解决方案:
We have,
A =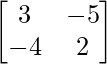
A2 =
=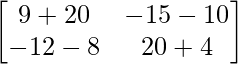
=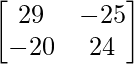
So, A2 – 5A – 14I =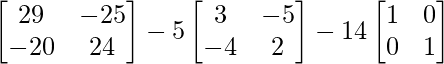
=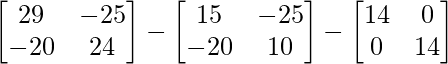
=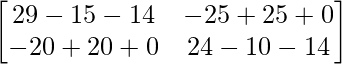
=
= 0
Now, as A2 – 5A – 14I = 0
=> A2 = 5A + 14I
=> A2 A = A (5A + 14I)
=> A3 = 5A2 + 14 AI
=> A3 = 5A2 + 14 A
=> A3 =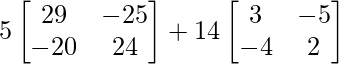
=> A3 =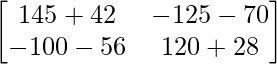
=> A3 =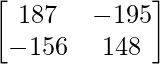
问题 54. 证明以下内容:
(i) 如果 P(x) = 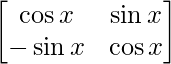 ,然后证明 P(x) P(y) = P(x+y) = P(y) P(x)。
,然后证明 P(x) P(y) = P(x+y) = P(y) P(x)。
解决方案:
We have,
P(x) =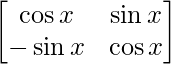
Now, P(x) P(y) =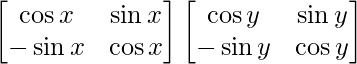
=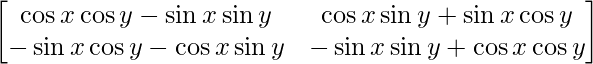
=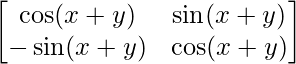
= P(x+y)
Also, P(y) P(x) =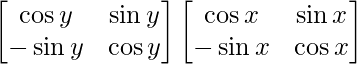
=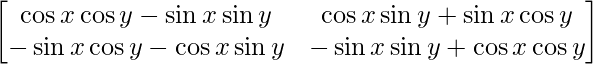
=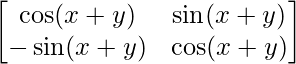
= P(x+y)
Therefore, P(x) P(y) = P(x+y) = P(y) P(x).
Hence proved.
(ii) 如果 P = 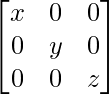 Q =
Q = 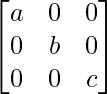 , 证明 PQ =
, 证明 PQ = 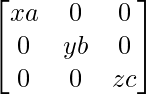 = QP。
= QP。
解决方案:
We have,
P =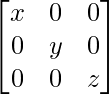 and Q =
and Q =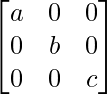
PQ =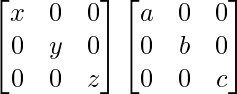
=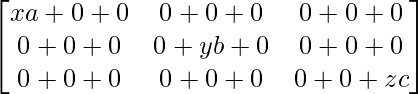
=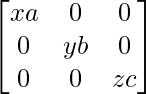
QP =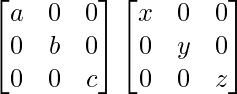
=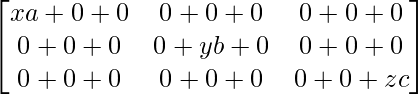
=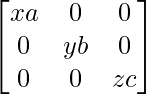
Therefore, PQ =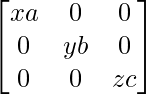 = QP.
= QP.
Hence proved.
问题 55. 如果 A = 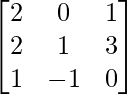 ,找到 A 2 – 5A + 4I 并找到一个矩阵 X 使得 A 2 – 5A + 4I + X = 0。
,找到 A 2 – 5A + 4I 并找到一个矩阵 X 使得 A 2 – 5A + 4I + X = 0。
解决方案:
We have,
A =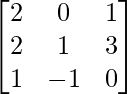
A2 =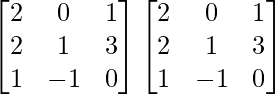
=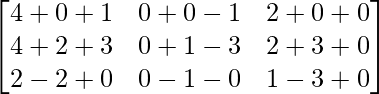
=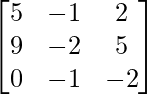
So, A2 – 5A + 4I =
=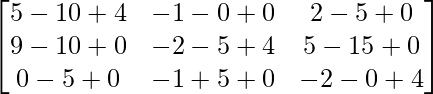
=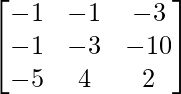
If A2 – 5A + 4I + X = 0, then
=> X = – (A2 – 5A + 4I)
=> X =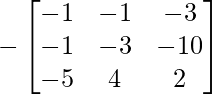
=> X =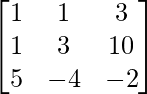
问题 56. 如果 A = 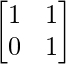 , 证明 A =
, 证明 A = 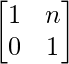 , 对于所有正整数 n。
, 对于所有正整数 n。
解决方案:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =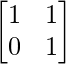
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =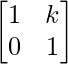
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=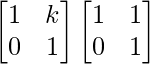
=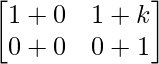
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
问题 57. 如果 A = 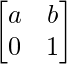 , 证明 A n =
, 证明 A n = 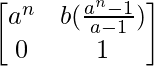 , 对于每个正整数 n。
, 对于每个正整数 n。
解决方案:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =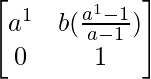
=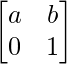
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =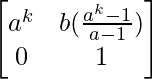
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=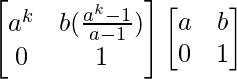
=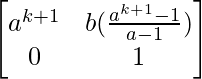
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
问题 58. 如果 A = 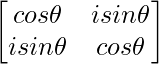 , 用数学归纳原理证明 A n =
, 用数学归纳原理证明 A n = 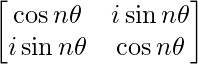 , 对于所有 n ∈ N。
, 对于所有 n ∈ N。
解决方案:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =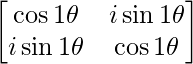
=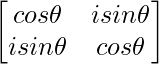
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =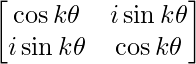
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=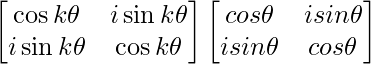
=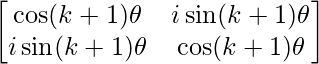
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
问题 59. 如果 A = 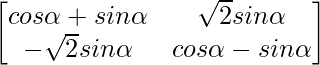 , 证明 A n =
, 证明 A n = 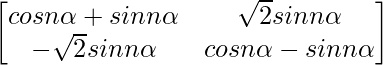 , 对于所有 n ∈ N。
, 对于所有 n ∈ N。
解决方案:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =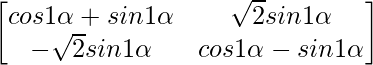
=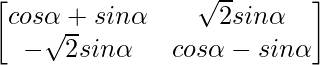
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=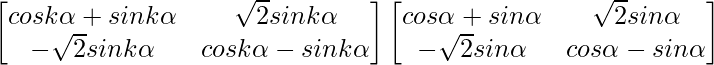
=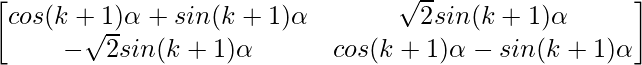
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
问题 60. 如果 A = 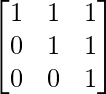 , 用数学归纳原理证明 A n =
, 用数学归纳原理证明 A n = 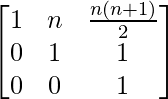 对于每个正整数 n。
对于每个正整数 n。
解决方案:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =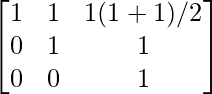
=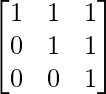
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =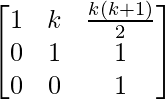
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=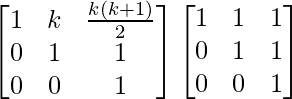
=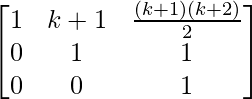
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
问题 61. 如果 B, C 是 n 行方阵,并且如果 A = B + C, BC = CB, C 2 = 0, 那么证明对于每个 n ∈ N, A n+1 = B n (B + (n +1)C)。
解决方案:
We are given,
A = B + C, BC = CB and C2 = 0
=> A2 = (B + C)2
=> A2 = B2 + C2 + 2 BC
=> A2 = B2 + 2 BC
=> A2 = B (B + 2C) . . . . (1)
We have to prove that An+1 = Bn (B + (n+1)C), for n ∈ N
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1+1 = B1 (B + (1+1)C)
A2 = B (B + 2C)
From (1) we get that the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak+1 = Bk (B + (k+1)C)
Step 3: For n = k + 1, we have
Ak+1+1 = Ak+2 = Ak A2
= Bk-1 (B + kC) B (B + 2C)
= Bk (B + kC) (B + 2C)
= Bk (B2 + 2BC + k CB + 2kC2)
= Bk (B2 + 2BC + k BC)
= Bk B (B + (k+2)C)
= Bk+1 (B + (k+2)C)
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
问题 62. 如果 A = diag (a, b, c),证明 A n = diag (a n , b n , c n ),对于所有正整数 n。
解决方案:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 = diag (a1, b1, c1)
A = diag (a, b, c)
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak = diag (ak, bk, ck)
Step 3: For n = k + 1, we have
Ak+1 = Ak A
= diag (ak, bk, ck) diag (a, b, c)
=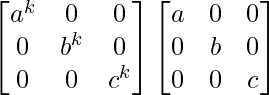
=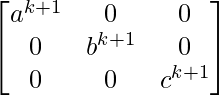
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
问题 63. 如果 A 是一个方阵,使用数学归纳法证明对于所有 n ∈ N 有 (A T ) N = (A N ) T。
解决方案:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
(AT)1 = (A1)T
AT = AT
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
(AT)K = (AK)T
Step 3: For n = k + 1, we have
(AT)K+1 = (AT)K (AT)1
= (AK)T (A1)T
= (AK+1)T
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
问题 64.矩阵 X 有 a + b 行和 a + 2 列,而矩阵 Y 有 b + 1 行和 a + 3 列。矩阵 XY 和 YX 都存在。找到 a 和 b。你能说 XY 和 YX 是同一类型吗?他们平等吗?
解决方案:
Here X is of order (a+b) × (a+2) and Y is of order (b+1) × (a+3).
If XY exists, we get
=> a + 2 = b + 1 . . . . (1)
And if YX exists, we get
=> a + b = a + 3
=> b = 3
Putting this in (1), we have
=> a + 2 = 3 + 1
=> a = 2
Since the order of the matrices XY and YX is not same, XY and YX are not of the same type and they are unequal.
问题 65. 举一个矩阵 A 和 B 的例子:
(一) AB≠BA
解决方案:
Let A =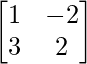 and B =
and B =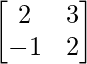
AB =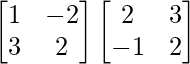
=
=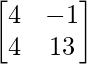
Now, BA =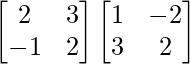
=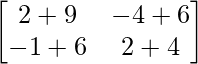
=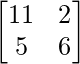
Thus, AB ≠ BA.
(ii) AB = O 但 A ≠ 0, B ≠ 0
解决方案:
Let A =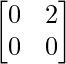 and B =
and B =
AB =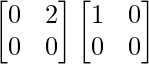
=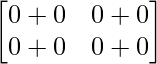
=
Thus, AB = O but A ≠ 0, B ≠ 0.
(iii) AB = O 但 BA ≠ O
解决方案:
Let A =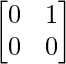 and B =
and B =
Here, AB = 0
But BA =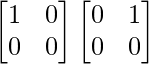
=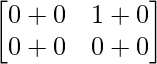
=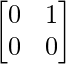
Thus, AB = O but BA ≠ O.
(iv) AB = AC 但 B ≠ C, A ≠ 0
解决方案:
Let A = , B =
, B = and C =
and C =
AB =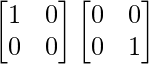
=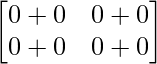
=
And AC =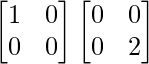
=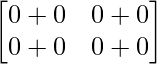
=
Thus, AB = AC but B ≠ C, A ≠ 0.
问题 66. 设 A 和 B 是相同阶的方阵。 (A + B) 2 = A 2 + 2AB + B 2成立吗?如果不是,为什么?
解决方案:
We have,
L.H.S. = (A + B)2
= (A + B) (A + B)
= A (A + B) + B (A + B)
= A2 + AB + BA + B2
Here AB ≠ BA as matrix does not have a commutative property.
Therefore, (A + B)2 ≠ A2 + 2AB + B2.
问题 67. 如果 A 和 B 是相同阶的方阵,请解释为什么一般
(i) (A + B) 2 ≠ A 2 + 2AB + B 2
解决方案:
We have,
L.H.S. = (A + B)2
= (A + B) (A + B)
= A (A + B) + B (A + B)
= A2 + AB + BA + B2
Here AB ≠ BA as in general matrix does not have a commutative property.
Therefore, (A + B)2 ≠ A2 + 2AB + B2.
(ii) (A – B) 2 ≠ A 2 – 2AB + B 2
解决方案:
We have,
L.H.S. = (A – B)2
= (A – B) (A – B)
= A (A – B) + B (A – B)
= A2 – AB – BA + B2
Here AB ≠ BA as in general matrix does not have a commutative property.
Therefore, (A – B)2 ≠ A2 – 2AB + B2.
(iii) (A + B) (A – B) ≠ A 2 – B 2
解决方案:
We have,
L.H.S. = (A + B) (A – B)
= A (A – B) + B (A – B)
= A2 – AB + BA – B2
Here AB ≠ BA as in general matrix does not have a commutative property.
Therefore, (A + B) (A – B) ≠ A2 – B2.
问题 68. 设 A 和 B 是 3 × 3 阶的方阵。 (AB) 2 = A 2 B 2吗?说明理由。
解决方案:
We know, (AB)2 = A2 B2, only if AB = BA
If AB = BA, then
(AB)2 = (AB) (AB)
On using associative law, we get
= A (BA) B
= A (AB) B
= A2 B2
Hence proved.
问题 69. 如果 A 和 B 是相同阶的方阵,使得 AB = BA,则证明 (A + B) 2 = A 2 + 2AB + B 2 。
解决方案:
We are given, AB = BA.
L.H.S. = (A + B)2
= (A + B) (A + B)
= A (A + B) + B (A + B)
= A2 + AB + BA + B2
= A2 + AB + BA + B2
= A2 + 2AB + B2
= R.H.S.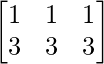
Hence proved.
问题 70. 让 A = 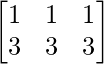 , B =
, B = 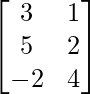 和 C =
和 C = 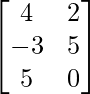 .验证 AB = AC 虽然 B ≠ C,A ≠ O。
.验证 AB = AC 虽然 B ≠ C,A ≠ O。
解决方案:
We have,
A =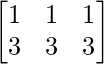 , B =
, B =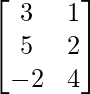 and C =
and C =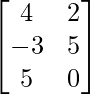
L.H.S. = AB
=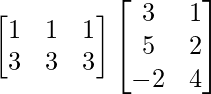
=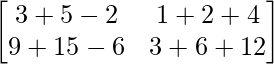
=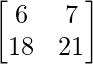
R.H.S. = AC
=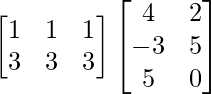
=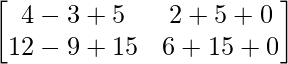
=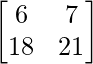
Therefore, L.H.S. = R.H.S.
Hence proved.
问题 71. 三个店主 A、B 和 C 去商店购买文具。 A 购买了 12 打笔记本、5 打钢笔和 6 打铅笔。 B 购买了 10 打笔记本、6 打钢笔和 7 打铅笔。 C 购买了 11 打笔记本、13 打钢笔和 8 打铅笔。一个笔记本需要 40 派萨,一支笔需要卢比。 1.25 和一支铅笔需要 35 派萨。使用矩阵乘法计算每个人的账单。
解决方案:
Cost of notebooks per dozen = (12 × 40) paise = Rs 4.80
Cost of pens per dozen = (12 × 1.25) paise = Rs 15
Cost of Pencils per dozen = (12 × 35) paise = Rs 4.20
So, we get
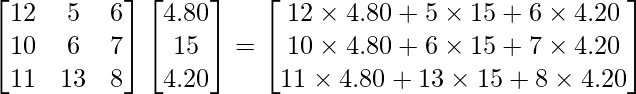
=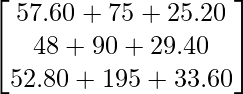
=
Therefore, the bills of A, B and C are Rs 157.80, Rs 167.40 and Rs 281.40, respectively.
问题72,某学校的合作书店有10打物理书、8打化学书和5打数学书。他们的售价是卢比。 8.30,卢比。 3.45 和卢比。各4.50。找出商店从出售所有商品中获得的总金额。
解决方案:
The stocks of various types of books in the store is given as,
Physics Chemistry Mathematics
X =![]()
Selling price of various types of books in the store is,
Y =
Total amount received by the store from selling all the items will be = XY
XY =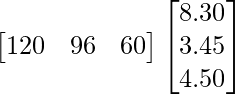
=![]()
=![]()
=![]()
Therefore, the total amount the store will receive from selling all the items is Rs 1597.20.
问题 73. 在立法议会选举中,一个政治团体聘请了一家公关公司以三种方式宣传其候选人:电话、上门拜访和信件。给定矩阵 A 的每个联系人的成本(以 paise 为单位)为
每次联系费用
一个= 
在两个城市 X 和 Y 中建立的每种类型的联系人数量在矩阵 B 中给出:
电话 出诊 信
乙 = 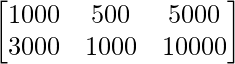
求该组在 X 和 Y 两个城市的消费总额。
解决方案:
The cost per contact (in paise) is given by
A =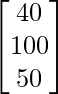
The number of contacts of each type made in the two cities X and Y is given by
Telephone House calls Letter
B =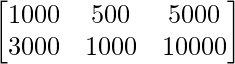
Total amount spent by the group in the two cities X and Y is given by
BA =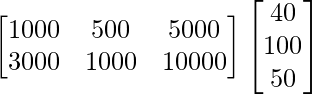
=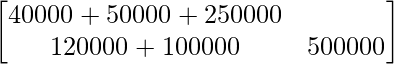
=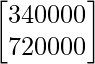
Thus, amount spent on X = Rs 3400 and amount spent on Y = Rs 7200.
问题 74。信托基金有 30000 卢比,必须投资于两种不同类型的债券。第一个债券每年支付 5% 的利息,第二个债券每年支付 7% 的利息。使用矩阵乘法,确定如何在两种债券中分配 30000 卢比。如果信托基金必须获得每年的总利息
(i) 1800 卢比
解决方案:
Suppose Rs x are invested in the first type of bond and Rs (30000 – x) are invested in the second type of bond, then
A =![]() represents investment and the matrix and B =
represents investment and the matrix and B =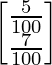 represents rate of interest
represents rate of interest
So, we get
=>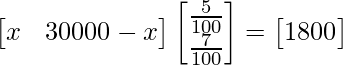
=>![]()
=>![]()
=> 210000 – 2x = 180000
=> 2x = 30000
=> x = 15000
Therefore, amount invested in the first bond = Rs 15000 and amount invested in the second bond = Rs (30000 – 15000) = Rs 15000.
(ii) 2000 卢比
解决方案:
Suppose Rs x are invested in the first type of bond and Rs (30000 – x) are invested in the second type of bond, then
A =![]() represents investment and the matrix and B =
represents investment and the matrix and B =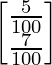 represents rate of interest
represents rate of interest
So, we get
=>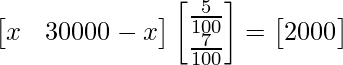
=>![]()
=>![]()
=> 210000 – 2x = 200000
=> 2x = 10000
=> x = 5000
Therefore, amount invested in the first bond = Rs 5000 and amount invested in the second bond = Rs (30000 – 5000) = Rs 25000.
问题 75. 为了促进为妇女建造厕所,一个组织试图通过 (i) 上门拜访 (ii) 信件和 (iii) 公告来提高认识。每种模式每次尝试的成本如下:
一世。卢比。 50
ii.卢比。 20
iii.卢比。 40
X、Y 和 Z 三个村庄的尝试次数如下: (i) (ii) (iii) X 400 300 100 Y 300 250 75 Z 500 400 150
使用矩阵分别找出组织为三个村庄产生的总成本。
解决方案:
Let A be the matrix showing number of attempts made in three villages X, Y and Z.
A =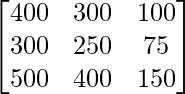
And, suppose B is a matrix showing the cost for each mode per attempt.
B =![]()
AB =
=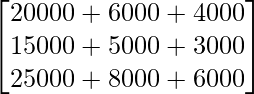
=
Therefore, the total cost incurred by the organisation for three villages X, Y and Z is 30,000 23,000 and 39,000 respectively.
问题76,A、B有2个家庭,A家庭有4男6女2小孩,B家庭有2男2女4小孩,建议男性每日热量2400,1900女性,儿童 1800 克,男性 45 克蛋白质,女性 55 克,儿童 33 克。用矩阵表示上述信息。使用矩阵乘法,计算两个家庭中每一个的卡路里和蛋白质的总需求。通过这个问题,你可以让人们对计划饮食产生什么认识?
解决方案:
Let X be the matrix showing number of family members in family A and B.
X =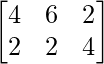
And, suppose Y is a matrix showing the recommend daily amount of calories.
Y =
And, Z be a matrix showing the recommend daily amount of proteins.
Z =![]()
Now, the total requirement of calories of the two families will be shown by XY.
XY =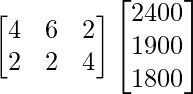
=![]()
=![]()
Also, the total requirement of proteins of the two families will be shown by XZ.
XZ =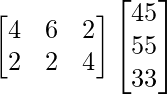
=![]()
=![]()
Therefore, the total requirement of calories and proteins for each of the two families is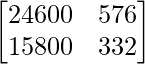 .
.
We must take balanced diet to stay healthy.
问题 77. 在议会选举中,一个政党聘请了一家公关公司以三种方式宣传其候选人——电话、上门拜访和信件。每次接触的成本(以派萨为单位)在矩阵 A 中给出为
一个= 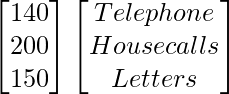
在两个城市 X 和 Y 中进行的每种类型的联系人的数量在矩阵 B 中给出为
电话 房屋 电话 信件
乙 = 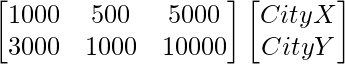
求该党在两个城市的消费总额。投票前应该考虑什么 - 政党对其社会活动的宣传活动?
解决方案:
Let A be the matrix showing the cost per contact (in paisa).
A =
And, B be a matrix showing the number of contacts of each type made in two cities X and Y.
Telephone House calls Letters
B =
Now, the total amount spent by the party in the two cities will be shown by BA.
BA =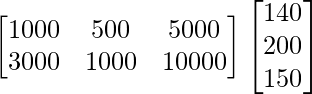
=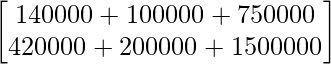
=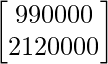
Therefore, the total amount spent by the party in the two cities X and Y is 9900 and 21200 respectively.
One should consider social activities of a party before casting his/her vote to that party.