第12类RD Sharma解–第19章不定积分–练习19.9 |套装2

📌 相关文章

📜 第12类RD Sharma解–第19章不定积分–练习19.9 |套装2

📅 最后修改于: 2021-06-24 17:29:25 🧑 作者: Mango

问题25.∫(1 +cos⁡x)/(((x +sin⁡x) ³ )dx

解决方案：

Given that I = ∫(1 + cos⁡x)/((x + sin⁡x)³) dx …..(i)

Let us considered x + sin⁡x = t then,

On differentiating both side we get,

d(x + sin⁡x) = dt

(1 + cos⁡x)dx = dt

Now on putting x + sin⁡x = t and (1 + cos⁡x)dx = dt in equation (i), we get

I = ∫ dt/t³

= ∫ t^-3 dt

= t^-2/-2 + c

= -1/(2t²) + c

= (-1)/(2(x + sin⁡x)²) + c

Hence, I = (-1)/(2(x + sin⁡x)²) + c

为什么编程需要懂一点英语

问题26.∫(cos⁡x–sin⁡x)/(1 +sin⁡2x)dx

解决方案：

Given that I = (cos⁡x – sin⁡x)/(1 + sin⁡2x)

= (cos⁡x – sin⁡x)/((sin²⁡x + cos²⁡x) + 2sin⁡xcos⁡x) [Because sin²⁡x + cos²⁡x = 1 and sin⁡2x = 2sin⁡xcos⁡x]

Let us considered sin⁡x + cos⁡x = t

On differentiating both side we get,

(cos⁡x – sin⁡x)dx = dt

Now,

= ∫(cos⁡x – sin⁡x)/(1 + sin⁡2x) dx

= ∫(cos⁡x – sin⁡x)/((sin⁡x + cos⁡x)²) dx

= ∫dt/t²

= ∫t^-2 dt

= -t^-1+ c

= -1/t + c

Hence, I = (-1)/(sin⁡x + cos⁡x) + c

为什么编程需要懂一点英语

问题27.∫(sin⁡2x)/(a +bcos⁡2x) ² dx

解决方案：

Given that I = ∫(sin⁡2x)/((a + bcos⁡2x)²) dx ……(i)

Let us considered a + bcos⁡2x = t then,

On differentiating both side we get,

(a + bcos⁡2x) = dt

b(-2sin⁡2x)dx = dt

sin⁡2x dx = -dt/2b

Now on putting a + bcos⁡2x = t and sin⁡2xdx = -dt/2b in equation (i), we get

I = ∫1/t²× (-dt)/2b

= (-1)/2b ∫ t^-2 dt

= -1/2b (-1t^-1) + c

= 1/2bt + c

= 1/(2b(a + bcos⁡2x)) + c

Hence, I = 1/(2b(a + bcos⁡2x)) + c

为什么编程需要懂一点英语

问题^{28.∫(log⁡x2)/} X DX

解决方案：

Given that I = ∫(log⁡x²)/x dx ……..(i)

Let us considered log⁡x = t then,

On differentiating both side we get,

d(log⁡x) = dt

1/x dx = dt

dx/x = dt

Now, I = ∫(log⁡x²)/x dx

= ∫(2log⁡x)/x dx

= 2∫(log⁡x)/x dx …….(ii)

Now on putting log⁡x = t and dx/x = dt in equation (ii), we get

I = 2∫tdt

= (2t²)/2 + c

= t²+ c

I = (log⁡x)²+ c

为什么编程需要懂一点英语

问题29.∫(sin⁡x)/(1 +cos⁡x) ² dx

解决方案：

Given that I = ∫(sin⁡x)/((1 + cos⁡x)²) dx …..(i)

Let us considered 1 + cos⁡x = t then,

On differentiating both side we get,

d(1 + cos⁡x) = dt

-sin⁡xdx = dt

sin⁡xdx = -dt

Now on putting 1 + cos⁡x = t and sin⁡dx = -dt in equation (i), we get

I = ∫(-dt)/t²

= -∫t^-2dt

= -(-1t^-1) + c

= 1/t + c

= 1/(1 + cos⁡x) + c

Hence, I = 1/(1 + cos⁡x) + c

为什么编程需要懂一点英语

问题30.∫cot⁡xlog⁡sin⁡xdx

解决方案：

Given that I = ∫cot⁡x log⁡ sin⁡x dx

Let us considered log⁡ sin⁡x = t

1/(sin⁡x).cos⁡xdx = dt

cot⁡x dx = dt

∫cot⁡x log⁡ sin⁡x dx = ∫tdt

= t²/2 + c

= 1/2(log⁡sin⁡x)²+ c

为什么编程需要懂一点英语

问题31.∫sec⁡x.log⁡(sec⁡x+tan⁡x)dx

解决方案：

Given that I = ∫sec⁡x.log⁡(sec⁡x + tan⁡x)dx ……..(i)

Let us considered log⁡(sec⁡x + tan⁡x) = t then,

On differentiating both side we get,

d[log⁡(sec⁡x + tan⁡x)] = dt

sec⁡x dx = dt [Since, d/dx(log⁡(sec⁡x + tan⁡x)) = sec⁡x]

Now on putting log⁡(sec⁡x + tan⁡x) = t and sec⁡x dx = dt in equation (i), we get

I = ∫tdt

= t²/2 + c

= 1/2[log⁡(sec⁡x + tan⁡x)]²+ c

Hence, I = 1/2[log⁡(sec⁡x + tan⁡x)]²+ c

为什么编程需要懂一点英语

问题32。∫cosec⁡xlog⁡(cosec⁡x–cot⁡x)dx

解决方案：

Given that I = ∫cosec⁡x log⁡(cosec⁡x – cot⁡x)dx ……(i)

Let us considered log⁡(cosec⁡x – cot⁡x) = t then,

On differentiating both side we get,

dx[log⁡(cosec⁡x – cot⁡x)] = dt

cosec⁡x dx = dt [ Since, d/dx(log⁡(cosec⁡x – cot⁡x)) = cosec⁡x]

Now on putting log⁡(cosec⁡x – cot⁡x) = t and cosec⁡xdx = dt in equation (i), we get

I = ∫tdt

= t²/2 + c

Hence, I = 1/2[log⁡(cosec⁡x – cot⁡x)]²+ c

为什么编程需要懂一点英语

问题^{^{33.∫x3cos⁡x4}} DX

解决方案：

Given that I = ∫x³cos⁡x⁴ dx …….(i)

Let us considered x⁴= t then,

On differentiating both side we get,

dx(x⁴) = dt

4x³dx = dt

x³= dt/4

Now on putting x⁴= t and x³dx = dt/4 in equation (i), we get

I = ∫ cos⁡t dt/4

= 1/4sint + c

Hence, I = 1/4sinx⁴+ c

为什么编程需要懂一点英语

问题^{^{34.∫x3sin⁡x4}} DX

解决方案：

Given that I = ∫x³sin⁡x⁴ dx …..(i)

Let us considered x⁴= t then,

On differentiating both side we get,

d(x⁴) = dt

4x³dx = dt

x³= dt/4

Now on putting x⁴= t and x³dx = dt/4 in equation (i), we get

I = ∫sin⁡t dt/4

= 1/4 ∫sin⁡t dt

= -1/4 cos⁡t + c

Hence, I = -1/4 cos⁡x⁴+ c

为什么编程需要懂一点英语

问题35.∫(xsin ^-1 x ² )/√(1 – x ⁴ )dx

解决方案：

Given that I = ∫(xsin^-1⁡x²)/√(1 – x⁴) dx …….(i)

Let us considered sin^-1x²= t then,

On differentiating both side we get,

d(sin^-1x²) = dt

2x × 1/√(1 – x⁴) dx = dt

x/√(1 – x⁴) dx = dt/2

Now on putting sin^-1x²= t and x/√(1 – x⁴) dx = dt/2 in equation (i), we get

I = ∫t dt/2

= 1/2 × t²/2 + c

= 1/4 (sin^-1x²)²+ c

Hence, I = 1/4 (sin^-1x²)²+ c

为什么编程需要懂一点英语

问题^{^{36.∫x3sin⁡(×4}} + 1)DX

解决方案：

Given that I = ∫x³ sin⁡(x⁴+ 1)dx ……..(i)

Let us considered x⁴+ 1 = t then,

On differentiating both side we get,

d(x⁴+ 1) = dt

x³ dx = dt/4

Now on putting x⁴+ 1 = t and x³dx = dt/4 in equation (i), we get

I = ∫ sin⁡t dt/4

= -1/4 cos⁡t + c

= -1/4 cos⁡(x⁴+ 1) + c

Hence, I = -1/4 cos⁡(x⁴+ 1) + c

为什么编程需要懂一点英语

问题37∫(X + 1)E ^X /(COS ^2⁡(XE ^x)的DX

解决方案：

Given that I = ∫((x + 1)e^x)/(cos²⁡(xe^x)) dx ……(i)

Let us considered xe^x= t then,

On differentiating both side we get,

d(xe^x) = dt

(e^x+ xe^x)dx = dt

(x + 1)e^xdx = dt

Now on putting xe^x= t and (x + 1)e^xdx = dt in equation (i), we get

I = ∫dt/(cos²⁡t)

= ∫ sec²tdt

= tan⁡t + c

= tan⁡(xe^x) + c

Hence, I = tan⁡(xe^x) + c

为什么编程需要懂一点英语

问题38。 $∫x^2 e^{x^3} cos⁡(e^{x^3})dx$

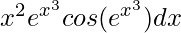
解决方案：

Given that I = $∫x^2 e^{x^3} cos⁡(e^{x^3})dx$ ……..(i)

Let us considered $e^{x^3}$ = t then,

On differentiating both side we get,

d( $e^{x^3}$ ) = dt

3x² $e^{x^3}$ dx = dt

x² $e^{x^3}$ dx = dt/3

Now on putting $e^{x^3}$ = t and x² $e^{x^3}$ dx = dt/3 in equation (i), we get

I = ∫cos⁡t dt/3

= (sin⁡t)/3 + c

Hence, I = sin⁡( $e^{x^3}$ )/3 + c

为什么编程需要懂一点英语

问题^{^{39.∫2xsec3(×2}} + ^3)tan⁡(×2 + 3)DX

解决方案：

Given that I = ∫2xsec³(x²+ 3)tan⁡(x²+ 3)dx ………(i)

Let us considered sec⁡(x²+ 3) = t then,

On differentiating both side we get,

d[sec⁡(x²+ 3)] = dt

2xsec⁡(x²+ 3)tan⁡(x²+ 3)dx = dt

Now on putting sec⁡(x²+ 3) = t and 2xsec⁡(x²+ 3)tan⁡(x²+ 3)dx = dt in equation (i), we get

I = ∫t² dt

= t³/3 + c

= 1/3 [sec⁡(x²+ 3)]³+ c

Hence, I = 1/3 [sec⁡(x²+ 3)]³+ c

为什么编程需要懂一点英语

问题40.∫(1 + 1 / x)(x +log⁡x) ² dx

解决方案：

Given that I = ((x + 1)(x + log⁡x)²)/x

= ((x + 1)/x)(x + log⁡x)²

= (1 + 1/x)(x + log⁡x)²

Let us considered (x + log⁡x) = t

On differentiating both side we get,

(1 + 1/x)dx = dt

Now,

I = ∫(1 + 1/x)(x + log⁡x)² dx

= ∫t² dt

= t³/3 + c

Hence, I = 1/3(x + log⁡x)³+ c

为什么编程需要懂一点英语

问题41.∫tan⁡x秒^2⁡x√(1 -褐色^2×)DX

解决方案：

Given that I = ∫tan⁡x sec²⁡x√(1 – tan²x) dx ………(i)

Let us considered 1 – tan²⁡x = t then,

On differentiating both side we get,

d(1 – tan²x) = dt

-2tan⁡x sec²⁡x dx = dt

tan⁡x sec²⁡x dx = (-dt)/2

Now on putting 1 – tan²x = t and tan⁡x sec²⁡x dx = -dt/2 in equation (i), we get

I = ∫√t × (-dt)/2

=-1/2 ∫t^1/2dt

=-1/2×t^3/2/(3/2) + c

=-1/3 t^3/2+ c

Hence, I = -1/3 [1 – tan²⁡x]^3/2+ c

为什么编程需要懂一点英语

问题42.∫log⁡x(sin⁡(1 +(log⁡x) ² )/ x dx

解决方案：

Given that I = ∫log⁡x (sin⁡(1 + (log⁡x)²)/x dx ……..(i)

Now on putting 1 + (log⁡x)²= t and (log⁡x)/x dx = dt/2 in equation (i), we get

I = ∫sin⁡t × dt/2

= 1/2 ∫ sin⁡tdt

= -1/2 cos⁡t + c

= -1/2 cos⁡[1 + (log⁡x)²] + c

Hence, I = -1/2 cos⁡[1 + (log⁡x)²] + c

为什么编程需要懂一点英语

问题43.∫1 / x ² ×(cos ² (1 / x))dx

解决方案：

Given that I = ∫ 1/x² × (cos²⁡(1/x))dx ……(i)

Let us considered 1/x = t then,

On differentiating both side we get,

d(1/x) = dt

(-1)/x²dx = dt

1/x²dx = -dt

Now on putting 1/x = t and 1/x²dx = -dt in equation (i), we get

I = ∫cos²t(-dt)

= -∫cos²tdt

= -∫(cos2t + 1)/2 dt

= -1/2 ∫cos⁡2t dt – 1/2 ∫dt

= -1/2 × (sin⁡2t)/2 – 1/2 t + c

= -1/4 sin⁡2t – 1/2 t + c

= -1/4 sin⁡2 × 1/x – 1/2 × 1/x + c

Hence, I = -1/4 sin⁡(2/x) – 1/2 (1/x) + c

为什么编程需要懂一点英语

问题44.∫秒⁴ xtan⁡xdx

解决方案：

Given that I = ∫sec⁴x tan⁡x dx ……(i)

Let us considered tan⁡x = t then,

On differentiating both side we get,

d (tan⁡x) = dt

sec²xdx = dt

dx = dt/sec²⁡x

Now on putting tan⁡x = t and dx = dt/(sec²⁡x) in equation (i), we get

I = ∫sec⁴x tan⁡x dt/(sec²⁡x)

= ∫ sec²x tdt

= ∫ (1 + tan²⁡x)tdt

= ∫(1 + t²)tdt

= ∫(t + t³)dt

= t²/2 + t⁴/4 + c

= (tan²⁡x)/2 + (tan⁴⁡x)/4 + c

Hence, I = 1/2 tan²⁡x + 1/4 tan⁴⁡x + c

为什么编程需要懂一点英语

问题^{^{45.∫(E√xcos⁡(E√x))/√xDX}}

解决方案：

Given that I = ∫(e^√x cos⁡(e^√x))/√x dx …….(i)

Let us considered e^√x= t then,

On differentiating both side we get,

d(e^√x) = dt

e^√x(1/(2√x))dx = dt

e^√x/√x dx = 2dt

Now on putting e^√x= t and e^√x/√x dx = 2dt in equation (i), we get

I = ∫ cos⁡t × 2dt

= 2∫ cos⁡tdt

= 2sin⁡t + c

= 2sin⁡(e^√x) + c

I = 2sin⁡(e^√x) + c

为什么编程需要懂一点英语

问题46.∫(cos ⁵ x)/(sin⁡x)dx

解决方案：

Given that I = ∫(cos⁵⁡x)/(sin⁡x) dx …..(i)

Let us considered sin⁡x = t then,

On differentiating both side we get,

d(sin⁡x) = dt

cos⁡x dx = dt

dx = dt/(cos⁡x)

Now on putting sin⁡x = t and dx = dt/(cos⁡x) in equation (i), we get

I = ∫(cos⁵⁡x)/t × dt/(cos⁡x)

= ∫(cos⁴⁡x)/t dt

= ∫(1 – sin²⁡x)²/t dt

= ∫(1 – t²)²/t dt

= ∫(1 + t⁴– 2t²)/t dt

= ∫1/t dt + ∫t⁴/t dt – 2∫t²/t dt

= log⁡|t| + t⁴/4 – (2t²)/2 + c

= log⁡|sin⁡x| + (sin⁴⁡x)/4 – sin²⁡x + c

Hence, I = 1/4 sin⁴x – sin²x + log⁡|sin⁡x| + c

为什么编程需要懂一点英语

问题47.∫(sin⁡√x)/√xdx

解决方案：

Given that I = ∫(sin⁡√x)/√x dx

Let us considered √x = t then,

On differentiating both side we get,

1/(2√x) dx = dt

1/√x dx = 2dt

Now,

I = ∫(sin⁡√x)/√x dx

= 2 ∫sint dt

= -2 cos⁡t + c

Hence, I = -2cos⁡√x + c

为什么编程需要懂一点英语

问题48.∫(((x + 1)e ^x )/(sin ² (xe ^x ))dx

解决方案：

Given that I = ∫((x + 1)e^x)/(sin²⁡(xe^x)) dx …….(i)

Let us considered xe^x= t then,

d(xe^x) = dt

(xe^x+ e^x)dx = dt

(x + 1)e^xdx = dt

Now on putting xe^x= t and (x + 1)e^x dx = dt in equation (i), we get

I = ∫dt/(sin²t)

= ∫cos⁡ec²t dt

= -cot + c

Hence, I = -cot⁡(xe^x) + c

为什么编程需要懂一点英语

问题25.∫(1 +cos⁡x)/(((x +sin⁡x) 3 )dx

问题26.∫(cos⁡x–sin⁡x)/(1 +sin⁡2x)dx

问题27.∫(sin⁡2x)/(a +bcos⁡2x) 2 dx

问题28.∫(log⁡x2)/ X DX

问题29.∫(sin⁡x)/(1 +cos⁡x) 2 dx

问题30.∫cot⁡xlog⁡sin⁡xdx

问题31.∫sec⁡x.log⁡(sec⁡x+tan⁡x)dx

问题32。∫cosec⁡xlog⁡(cosec⁡x–cot⁡x)dx

问题33.∫x3cos⁡x4 DX

问题34.∫x3sin⁡x4 DX

问题35.∫(xsin -1 x 2 )/√(1 – x 4 )dx

问题36.∫x3sin⁡(×4 + 1)DX

问题37∫(X + 1)E X /(COS 2⁡(XE x)的DX

问题38。

问题39.∫2xsec3(×2 + 3)tan⁡(×2 + 3)DX

问题40.∫(1 + 1 / x)(x +log⁡x) 2 dx

问题41.∫tan⁡x秒2⁡x√(1 -褐色2×)DX

问题42.∫log⁡x(sin⁡(1 +(log⁡x) 2 )/ x dx

问题43.∫1 / x 2 ×(cos 2 (1 / x))dx

问题44.∫秒4 xtan⁡xdx

问题45.∫(E√xcos⁡(E√x))/√xDX

问题46.∫(cos 5 x)/(sin⁡x)dx

问题47.∫(sin⁡√x)/√xdx

问题48.∫(((x + 1)e x )/(sin 2 (xe x ))dx

问题25.∫(1 +cos⁡x)/(((x +sin⁡x) ³ )dx

问题27.∫(sin⁡2x)/(a +bcos⁡2x) ² dx

问题^{28.∫(log⁡x2)/} X DX

问题29.∫(sin⁡x)/(1 +cos⁡x) ² dx

问题^{^{33.∫x3cos⁡x4}} DX

问题^{^{34.∫x3sin⁡x4}} DX

问题35.∫(xsin ^-1 x ² )/√(1 – x ⁴ )dx

问题^{^{36.∫x3sin⁡(×4}} + 1)DX

问题37∫(X + 1)E ^X /(COS ^2⁡(XE ^x)的DX

问题38。 $∫x^2 e^{x^3} cos⁡(e^{x^3})dx$

问题^{^{39.∫2xsec3(×2}} + ^3)tan⁡(×2 + 3)DX

问题40.∫(1 + 1 / x)(x +log⁡x) ² dx

问题41.∫tan⁡x秒^2⁡x√(1 -褐色^2×)DX

问题42.∫log⁡x(sin⁡(1 +(log⁡x) ² )/ x dx

问题43.∫1 / x ² ×(cos ² (1 / x))dx

问题44.∫秒⁴ xtan⁡xdx

问题^{^{45.∫(E√xcos⁡(E√x))/√xDX}}

问题46.∫(cos ⁵ x)/(sin⁡x)dx

问题48.∫(((x + 1)e ^x )/(sin ² (xe ^x ))dx