第 12 课 NCERT 解决方案 - 数学第一部分 - 第 2 章反三角函数 - 练习 2.2 |设置 2

第 2 章反三角函数 – 练习 2.2 |设置 1

找出以下各项的值：

问题 11. tan ^-1 [2cos(2sin ^-1 1/2​)]

解决方案：

Let us assume that sin⁻¹1/2 = x

So, sinx = 1/2

Therefore, x = π​/6 = sin⁻¹1/2

Therefore, tan⁻¹[2cos(2sin⁻¹1/2​)] =  tan⁻¹[2cos(2 * π​/6)]

= tan⁻¹[2cos(π​/3)]

Also, cos(π/3​) = 1/2​

Therefore, tan⁻¹[2cos(π​/3)] = tan⁻¹[(2 * 1/2)]

= tan⁻¹[1] = π​/4 

问题 12. cot(tan ^-1 a + cot ^-1 a)

解决方案：

We know, tan⁻¹x + cot⁻¹x = π​/2

Therefore, cot(tan⁻¹a + cot⁻¹a) = cot(π​/2) =0

问题 13。 $tan\frac{1}{2}[sin^{-1}\frac{2x}{1+x^2}+cos^{-1}\frac{1-y^2}{1+y^2}],|x|<1,y>0,xy<1$

解决方案：

We know, 2tan^-1x = $sin^{-1}\frac{2 x}{1+x^2}$ and 2tan^-1y =  $cos^{-1}[\frac{1 - y^2 }{1+y^2}]$

$\therefore tan\frac{1}{2}[sin^{-1}\frac{2x}{1+x^2}+cos^{-1}\frac{1-y^2}{1+y^2}]$ 

= tan(1/2)​[2(tan⁻¹x + tan⁻¹y)]

= tan[tan⁻¹x + tan⁻¹y]

Also, tan⁻¹x + tan⁻¹y = $tan^{-1}\frac{x+y}{1-xy}$

Therefore, tan[tan⁻¹x + tan⁻¹y] = $tan[tan^{-1}\frac{x+y}{1-xy}]$

= (x + y)/(1 – xy)

问题 14. 如果 sin(sin ⁻¹ 1/5​ + cos ⁻¹ x) = 1 那么求 x 的值

解决方案：

sin⁻¹1/5​ + cos⁻¹x = sin⁻¹1

We know, sin⁻¹1 = π/2

Therefore, sin⁻¹1/5​ + cos⁻¹x = π/2

sin⁻¹1/5​ = π/2 – cos⁻¹x

Since, sin⁻¹x​ + cos⁻¹x = π/2

Therefore, π/2 – cos⁻¹x = sin⁻¹x

sin⁻¹1/5​ = sin⁻¹x

So, x = 1/5

问题 15. 如果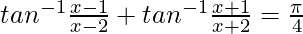$tan^{-1}\frac{x-1}{x-2} + tan^{-1}\frac{x+1}{x+2} = \frac{\pi}{4}$ ，然后找到 x 的值

解决方案：

We know, tan⁻¹x + tan⁻¹y = $tan^{-1}\frac{x+y}{1-xy}$

$tan^{-1}\frac{x-1}{x-2} + tan^{-1}\frac{x+1}{x+2} =tan^{-1}\frac{\frac{x-1}{x-2}+\frac{x+1}{x+2}}{1-\frac{x-1}{x-2}.\frac{x+1}{x+2}} = \frac{\pi}{4}$

$tan^{-1}\frac{\frac{(x-1)(x+2)+(x+1)(x-2)}{(x-2)(x+2)}}{\frac{(x-2)(x+2)-(x+1)(x-1)}{(x-2)(x+2)}} = \frac{\pi}{4}$

$tan^{-1}\frac{(x-1)(x+2)+(x+1)(x-2)}{(x-2)(x+2)-(x+1)(x-1)} = \frac{\pi}{4}$

$tan^{-1}(\frac{x^2+2x-x-2+x^2-2x+x-2}{x^2-4-x^2+1}) = \frac{\pi}{4}$

$tan^{-1}(\frac{x^2+x-2+x^2-x-2}{-3}) = \frac{\pi}{4}$

$tan^{-1}(\frac{2x^2-4}{-3}) = \frac{\pi}{4}$

$\frac{2x^2-4}{-3} = tan(\frac{\pi}{4})$

$\frac{2x^2-4}{-3} = 1$

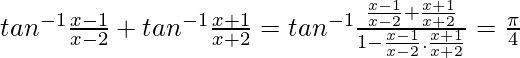
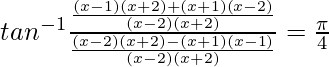
2x² – 4 = -3

2x² – 4 + 3 = 0

2x² – 1 = 0

x² = 1/2

x = 1/√2, -1/√2

找出练习 16 到 18 中每个表达式的值。

问题 16. sin ^{- 1} (sin2π/3​)

解决方案：

We know that sin⁻¹(sinθ) = θ when θ ∈ [-π/2, π/2], but $\frac{2 \pi}{3} > \frac{\pi}{2}$

So, sin ^{− 1}(sin2π/3​) can be written as $sin^{-1}[sin(\pi-\frac{2\pi}{3})]$

 sin ^{− 1}(sinπ/3​)  here $\frac{-\pi}{2}<\frac{\pi}{3}<\frac{\pi}{2}$

Therefore, sin ^{− 1}(sinπ/3​) = π/3

问题 17. tan ⁻¹ (tan3π/4​)

解决方案：

We know that tan⁻¹(tanθ) = θ when $\theta \epsilon(\frac{-\pi}{2},\frac{\pi}{2})$ but $\frac{3 \pi}{4} > \frac{\pi}{2}$

So, tan⁻¹(tan3π/4​) can be written as tan⁻¹(-tan(-3π/4)​)

= tan⁻¹[-tan(π – π/4​)]

= tan⁻¹[-tan(π/4​)]

= –tan⁻¹[tan(π/4​)]

= – π/4 where $\frac{-\pi}{4} \epsilon(\frac{-\pi}{2},\frac{\pi}{2})$

问题 18。 $tan(sin^{-1}\frac{3}{5} + cot^{-1}\frac{3}{2})$

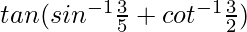
解决方案：

Let us assume $sin^{-1}\frac{3}{5}$ = x , so sinx = 3/5 

We know, $cosx = \sqrt{1-sin^2x}$

$\therefore cosx = \sqrt{1-(\frac{3}{5})^2}$

$cosx = \sqrt{1-\frac{9}{25}}$

$cosx = \sqrt{\frac{25-9}{25}}$

$cosx = \sqrt{\frac{16}{25}}$

cosx = 4/5

We know, $tanx = \frac{sinx}{cosx}$

So, $tanx = \frac{\frac{3}{5}}{\frac{4}{5}}$

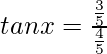
tanx = 3/4

Also, $tan^{-1}\frac{1}{x} = cot^{-1}x$

Hence, $tan(sin^{-1}\frac{3}{5} + cot^{-1}\frac{3}{2}) = tan(tan^{-1}\frac{3}{4}+tan^{-1}\frac{2}{3})$

tan^-1x + tan^-1y = $tan^{-1}\frac{x+y}{1-xy}$

So, $tan(tan^{-1}\frac{3}{4}+tan^{-1}\frac{2}{3}) = tan(tan^{-1}\frac {\frac{3}{4}+\frac{2}{3}}{1-\frac{3}{4}.\frac{2}{3}})$

$= tan(tan^{-1}\frac{\frac{9+8}{12}}{\frac{12-6}{12}})$

$= tan(tan^{-1}\frac{17}{6})$

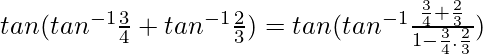
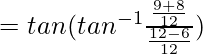
= 17/6

问题 19. cos ⁻¹ (cos7π/6​) 等于

(i) 7π/6 (ii) 5π/6 (iii)π/3 (iv)π/6

解决方案：

 We know that cos⁻¹(cosθ) = θ, θ ∈ [0, π]

cos⁻¹(cosθ) = θ, θ ∈ [0, π]

Here, 7π/6 > π 

So, cos⁻¹(cos7π/6​) can be written as cos⁻¹(cos(-7π/6)​)

= cos⁻¹[cos(2π – 7π/6​)]      [cos(2π + θ) = θ]

= cos⁻¹[cos(5π/6​)]       where 5π/6 ∈  [0, π]

  Therefore, cos⁻¹[cos(5π/6​)] = 5π/6 

问题 20。 $sin[\frac{\pi}{3} - sin^{-1}(-\frac{1}{2} )]$

(i) 1/2 (ii) 1/3 (iii) 1/4 (iv) 1

解决方案：

Let us assume sin^-1(-1/2)= x, so sinx = -1/2 

Therefore, x = -π/6​

Therefore, sin[π/3​ – (-π/6​)]

= sin[π/3​ + (π/6​)]

= sin[3π/6]

= sin[π/2]

= 1

问题 21。 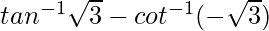$tan^{-1}\sqrt{3} - cot^{-1}(-\sqrt{3})$等于

(i) π (ii) -π/2 (iii)0 (iv)2√3

解决方案：

We know, cot(−x) = −cotx

Therefore, tan^-13 – cot^-1(-3) = tan^-13 – [-cot^-1(3)]

= tan^-13 + cot^-13

Since, tan^-1x + cot^-1x = π/2

Tan^-13 + cot^-13 = -π/2